Методы описания и анализа систем управления. Описание и анализ линейных систем с помощью дифференцианых уравнений.

Для анализа системы автоматического управления и регулирования необходимо располагать ее математическим описанием. Система может описываться Дифференциальными или интегро-дифференциальными уравнениями, уравнениями в частных производных и т. д. Они определяют поведение САУ в переходном процессе.

Уравнения называют уравнениями динамики, если они описывают изменение входящих в них переменных во времени. Из уравнений динамики можно получить уравнения статики, если положить входящие в них производные и воздействия равными нулю или постоянными величинами. Уравнения статики описывают поведение системы в установившемся режиме.

В соответствии с классификацией систем управления (рис. 24) кратко рассмотрим методы решения задач описания, анализа и синтеза линейных и нелинейных непрерывных систем управления. Сюда относят методики решения задач 1 анализа выходных процессов, устойчивости, управляемости и наблюдаемости линейных САУ. При этом используются все известные формы математического описания систем: дифференциальными уравнениями, переходными функциями, интегральными и спектральными преобразованиями.

В основе лежит представление системы в виде соединений образующих ee звеньев: последовательного, параллельного, с обратной связью, и замена сложной структуры эквивалентным звеном - оператором системы, преобразующим входной сигнал в выходной.

При исследовании нелинейных систем рассматривают задачи анализа выходных процессов при детерминированных и случайных воздействиях, анализа, абсолютной устойчивости нелинейной САУ; применяются методы гармонической и статистической линеаризации.

К современным проблемам управления можно отнести разработку методики решения задач оптимального управления детерминированными и стохастическими системами с применением принципа максимума и уравнения Беллмана, а также разработку алгоритмов синтеза систем совместного оценивания (наблюдателей состояния) и управления.

11.1. Линейные системы управления

11.1.1. Описание и анализ линейных систем с помощью дифференциальных уравнений

11.1.1.1. Одномерные системы при детерминированных воздействиях

Непрерывные процессы, протекающие в таких системах управления, описываются обыкновенными дифференциальными уравнениями (ОДУ) с соответствующими начальными условиями. Тогда, если известен вид входного сигнала, выходной сигнал определяется в результате решения задачи Коши для ОДУ.

Линейная нестационарная система описывается уравнением

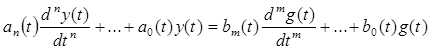(11.1)

с начальными условиями

(11.2)

где g(t) - входной сигнал, y(t) - выходной сигнал, t - текущее время, а_i (t), b_j(t)- коэффициенты уравнения.

Если коэффициенты а_i (t), b_j(t) уравнения (11.1) постоянны, система называется линейной стационарной.

Уравнение (11.1) может быть записано в операторной форме:

(11.3)

где оператор дифференцирования, D(p,t) и M(p,t) - собственный и входной операторы уравнения (11.1).

Для линейной стационарной системы уравнение в операторной форме имеет вид

(11.4)

Из операторной формы записи уравнения следует способ изображения стационарной системы (ее звеньев) на структурных схемах (рис. 27).

Рис. 27. Структурная схема стационарной системы

W(p)называют передаточной функцией. Строгое определение передаточной функции вводится через преобразование Лапласа при нулевых начальных условиях.

Звено любого физического вида и конструкции, описываемое дифференциальным уравнением или передаточной функцией первого и второго порядка называют типовым динамическим звеном. Описание типовых динамических звеньев рассматривается в курсе теории автоматического регулирования и управления.

По дифференциальным уравнениям типовых звеньев и связям между ними составляются структурные схемы систем. Они служат одним из языков описания систем управления.

Рассмотрим в качестве примера дифференциальное уравнение инерционного звена первого порядка:

Преобразуем это уравнение. Старшую производную (в данном случае производная одна) оставляем слева, остальные слагаемые переносим в правую часть:

Далее построим структурную схему (рис. 28)

y₀

–

Рис. 28. Инерционное звено первого порядка

Методика представления САУ в виде структурных схем используется, в частности, при решении задач с помощью аналоговой и цифровой вычислительной техники.

По структурной схеме всегда можно составить дифференциальные уравнения системы.

Анализ выходных процессов может быть проведен по результатам решения дифференциальных уравнений аналитическими методами, численными методами на ЭВМ или интегрированием дифференциальных уравнений по структурным схемам на аналоговой вычислительной технике.

Для линейных систем справедлив принцип суперпозиции: эффект, вызываемый суммой нескольких воздействий, равен сумме эффектов каждого из воздействий в отдельности. Поэтому выходной сигнал линейной САУ при аналитическом решении представляется в виде суммы свободного и вынужденного движений:

(11.5)