Упражнение 1.9.

Решение. Решая систему , находим координаты точки пересечения

графиков . Для определения угла находим производные в этой точке

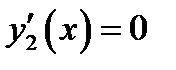; и применяем формулу (1.4).

Следовательно .

Упражнение 1.10.

Решение. Определяем положение точки в момент времени

. Скорость точки в этот момент равна

.

Упражнение 1.11. 1) Вторая производная это производная от первой производной

Вычисляем первую производную ;

Вычисляем вторую производную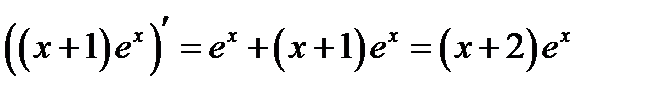

Ответ: .

Ответы: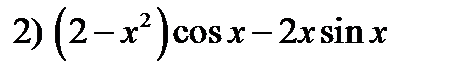

Дифференцирование сложной функции. Цепное правило.

Ответы и решения.

Упражнение2.2.

Ответы. 1)

Упражнение 2.3.

Ответы.

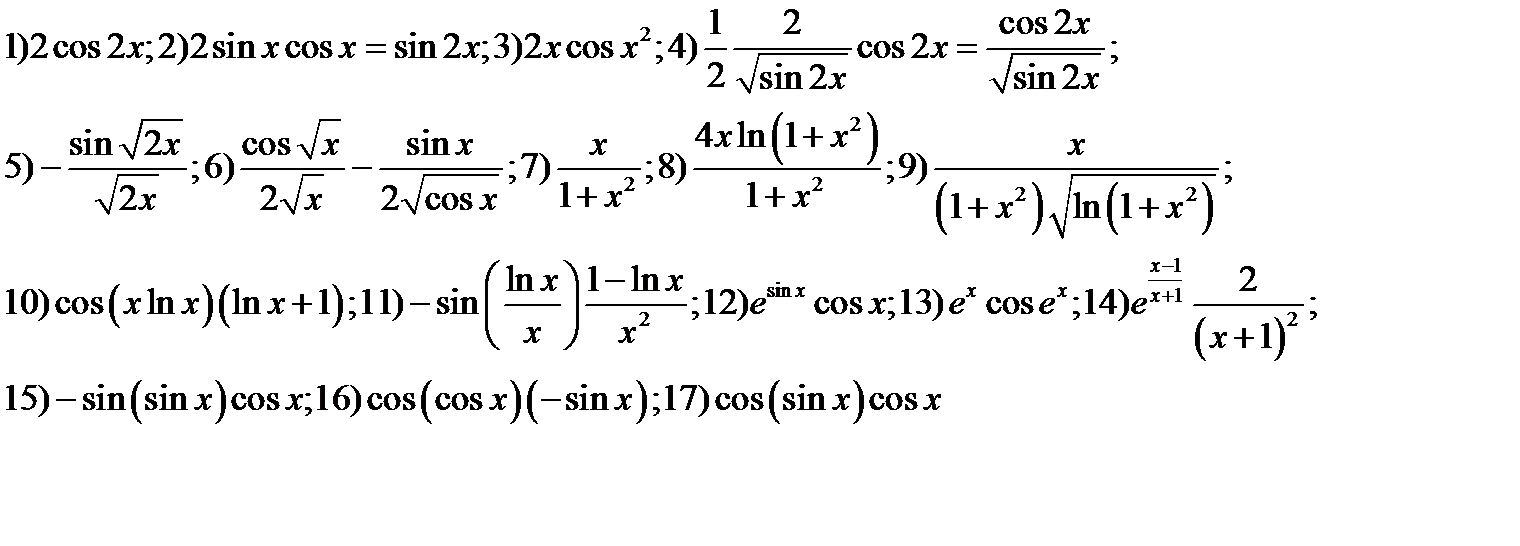
Упражнение 2.4. 1)1.06;2) -1.73 ; 3) 3;

Упражнение 2.5. ;

Упражнение 2.7.

Упражнение 2.8. для вычисления угла между касательными нам потребуется

1)угол наклона касательной в точке . ;

2)угол наклона касательной в точке . .

Отсюда

Неявное и параметрическое задание функций

Ответы к упражнениям.

Упражнение 3.1. 1)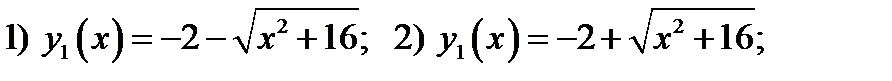

Упражнение 3.3. Решение.

1) дифференцируем уравнение задающее функцию

Ответ.

2) решая квадратное уравнение, находим явные выражения

. Принимая во внимание дополнительное условие

находим явное выражение функции 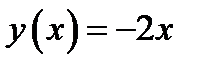. Вычисляя производную

получаем . Результаты совпали.