Упражнение 3.5.

Решение. 1).Применяя правило неявного дифференцирования, получаем

уравнение для определения первой производной .

Для вычисления второй производной, повторно применяем правило неявного

дифференцирования

2).Применяя правило неявного дифференцирования, получаем

уравнение для определения первой производной

.

Для вычисления второй производной, повторно применяем правило неявного

дифференцирования

Отсюда находим вторую производную

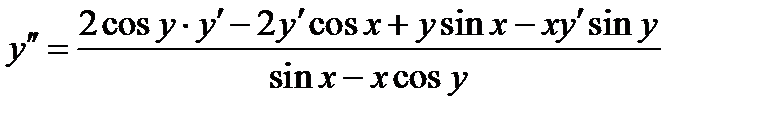
Упражнение 3.6.Для решения упражнения применяем формулы (3.8),(3.10)

Решение. Вычисляем ; . Далее согласно формуле (3.8) 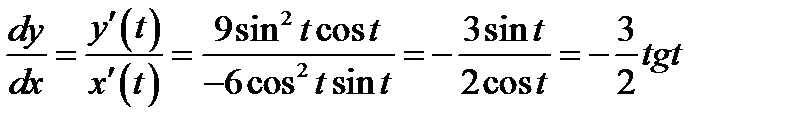и параметрическая запись производной принимает вид

Для записи в параметрическом виде второй производной используем формулу (3.10).

Вычисляем производную по параметру . Обозначим . Тогда

.

Отсюда параметрическая запись второй производной имеет вид

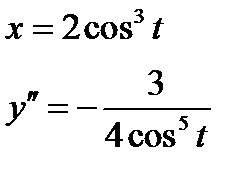
Упражнение 3.7.Применяя формулу (3.8) получаем ответы