КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теорема Коши
Рассмотрим, наконец, третью теорему о среднем, принадлежащей Коши (1789–1859), которая является обобщением теоремы Лагранжа.
Теорема. Если функции 
и 
непрерывны на отрезке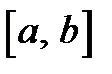 
и дифференцируемы во всех его внутренних точках, причем 
не обращается в ноль ни в одной из указанных точек, то существует, по крайней мере, одна точка 
, в которой 
.
Доказательство. Так как 
во всех точках 
, то отсюда следует, что 
. В противном случае, как следует из теоремы Ролля, существовала хотя бы одна точка 
, в которой 
.
Составим вспомогательную функцию
.
Данная функция непрерывна на отрезке 
и дифференцируема во всех его внутренних точках. Кроме того, вычисление ее в точках 
и 
дает: 
. Значит, функция 
удовлетворяет требованиям теоремы Ролля, то есть существует хотя бы одна точка 
, в которой 
.
Вычислим производную 
:
.
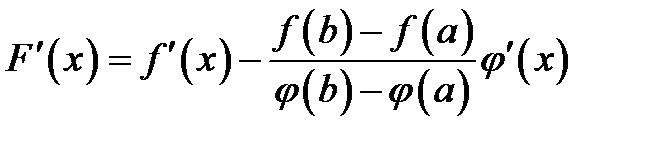Из условия 
следует, что
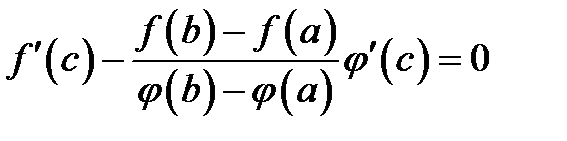и 
,
что и требовалось доказать.
В случае, когда 
, теорема Коши переходит в формулировку теоремы Лагранжа.
Правило Лапиталя-Бернули (раскрытие неопределенностей вида ∞/∞ и 0/0)
Теорема Лопита́ля (также правило Бернулли — Лопиталя) — метод нахождения пределов функций, раскрывающий неопределённости вида 0/0 и ∞/∞. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
Для раскрытия неопределённостей типа ∞/∞ используется следующий алгоритм:
Выявление старшей степени переменной;
Деление на эту переменную как числителя, так и знаменателя.
Для раскрытия неопределённостей типа 0/0 существует следующий алгоритм:
Разложение на множители числителя и знаменателя;
Сокращение дроби.
Неопределенности типа 
Пусть заданы две функции f (x) и g (x), такие, что
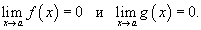
В этом случае говорят, что функция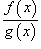 
имеет неопределенность типа в точке x = a. Чтобы найти предел при x = a когда функция 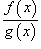содержит неопределенность , нужно разложить на множители числитель и/или знаменатель и затем сократить члены, стремящиеся к нулю.
Примечание: В данном разделе при вычислении пределов не используется правило Лопиталя.
Неопределенности типа 
Пусть две функции f (x) и g (x) обладают свойством
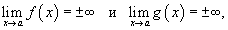
где a является действительным числом, либо стремится к + ∞ или − ∞. Говорят, что в этом случае функция 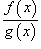имеет в точке a неопределенность типа . Для вычисления предела в этой точке необходимо разделить числитель и знаменатель на x в наивысшей степени.
Неопределенности типа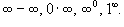 
Неопределенности этих типов сводятся к рассмотренным выше неопределенностям типа и .
Раскрытие неопределенностей вида 0 ∙ ∞; ∞-∞; 00; 1∞; ∞0
Также для вычисления пределов часто используется разложение выражений, входящих в исследуемую неопределённость, в ряд Тейлора в окрестности предельной точки. Для раскрытия неопределённостей видов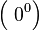 
, 
, 
пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.
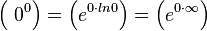
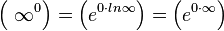
Для раскрытия неопределённостей типа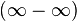 
иногда удобно применить следующее преобразование:
Пусть 
и 
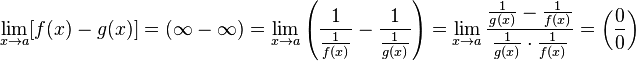
Формула Тейлора n-ого порядка, (теорема)
Формула Маклорена n-ого порядка, (теорема)
Формула Маклорена n-ого порядка для функций вида: sinx, cosx, ex; ln(1+x); (1+x)α; 1/(1+x); 1/(1-x)
Возрастание и убывание функции, (определение; необходимое и достаточное условие возрастания (убывания) функции на некотором промежутке)
Если производная некоторой непрерывной функции f(x) на некотором промежутке положительна (f'(x)>0), то на этом промежутке функция возрастает.
Если производная некоторой непрерывной функции f(x) на некотором промежутке отрицательна (f'(x)<0), то на этом промежутке функция убывает.
Эти условия являются достаточными условиями возрастания (убывания функции).
Постараемся понять, почему так происходит (строгое доказательство рассматривается в программе высших учебных заведений). Известно, что геометрический смысл производной - тангенс угла наклона касательной. Значит, если производная положительна, то угол будет острым.
И получается, что график идет «в гору». Если производная отрицательна, то угол наклона будет тупым и получается, что график идет «под гору».
Промежутки возрастания и убывания называют промежутками монотонности функции.
Точка x0 называется точкой максимума функции f(x), если существует положительное число E, такое, что для любой точки x из промежутка 
, выполняется неравенство 
. Иными словами, значение функции f(x0) самое большое в некоторой окрестности точки x0.
Точка x0 называется точкой минимума функции f(x), если существует положительное число E, такое, что для любой точки x из промежутка , выполняется неравенство 
. Иными словами значение функции f(x0) самое маленькое в некоторой окрестности точки x0.
На следующем графике точки -9 и 3 являются точками максимума, а точка -2 является точкой минимума.
Точки максимума или минимума называются точками экстремума.
Необходимое условие экстремума дифференцируемой функции. Достаточные условия существования экстремума (по первой производной)
Теорема Ферма: Если x0 - точка экстремума непрерывной функции f(x), то f'(x0)=0.
Геометрически это выглядит так: в точке экстремума касательная параллельна оси ОХ и, поэтому угол наклона равен 0.
Это условие является необходимым, но не достаточным условием экстремума.Достаточное условие экстремума: Если при переходе через стационарную точку производная меняет знак, то эта точка является экстремумом. Если меняет знак с «+» на «-», то это точка максимума. Если меняет знак с «-» на «+», то это точка минимума.
Если при переходе через стационарную точку производная не меняет знак, то эта точка не является экстремумом.
Дата добавления: 2015-04-18; просмотров: 296; Мы поможем в написании вашей работы!; Нарушение авторских прав |