Теорема Лагранжа

Результаты теоремы Ролля используются при рассмотрении следующей теоремы о среднем, принадлежащей Лагранжу (1736–1813).

Теорема. Если функция непрерывна на отрезке 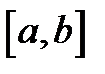и дифференцируема во всех его внутренних точках, то существует, по крайней мере, одна точка , в которой .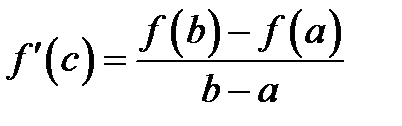

Доказательство. Рассмотрим график функции 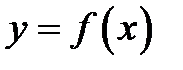(рис. 2.1).

Проведем хорду, соединяющую точк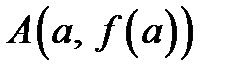и и 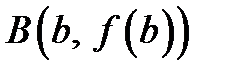, и запишем ее уравнение. Воспользовавшись уравнением прямой, проходящей через две точки на плоскости, получим:

,

откуда:

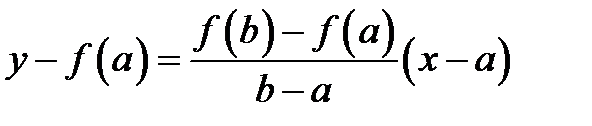и .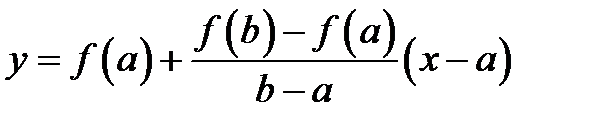

Составим теперь вспомогательную функцию, вычтя из уравнения кривой уравнение хорды:

.

Полученная функция 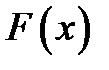непрерывна на отрезке 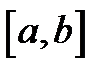и дифференцируема во всех его внутренних точках. Кроме того, вычисление 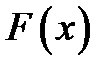в точках и 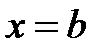показывает, что 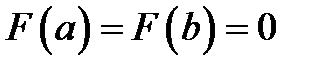. Значит, функция на отрезке удовлетворяет требованиям теоремы Ролля. Но в этом случае существует такая точка 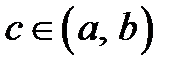, в которой .

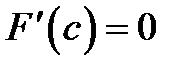Вычислим производную функции :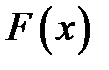

.

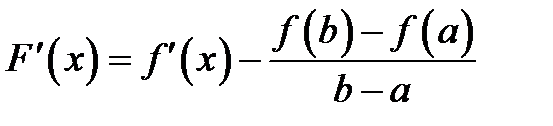Согласно теореме Ролля в точке 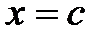производная 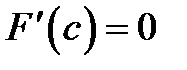, то есть 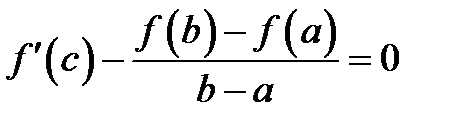и

,

что и требовалось доказать.

Геометрический смысл теоремы Лагранжа следующий: внутри отрезка 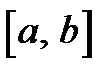существует, по крайней мере, одна точка, в которой касательная параллельна хорде, стягивающей кривую на данном отрезке. В частности, при 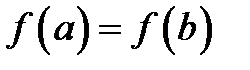теорема переходит в теорему Ролля.

Теорему Лагранжа часто записывают в следующем виде:

,

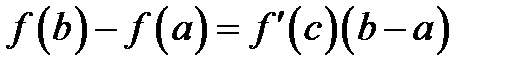то есть приращение функции равно приращению аргумента, умноженному на производную функции в некоторой внутренней точке. В связи с этим теорему Лагранжа называют также теоремой о конечных приращениях.