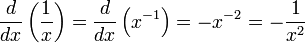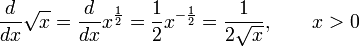КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Логарифмическое дифференцирование
Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием позволяет эффективно вычислять производные степенных и рациональных функций.
Рассмотрим этот подход более детально. Пусть дана функция y = f(x). Возьмем натуральные логарифмы от обеих частей: 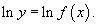
Теперь продифференцируем это выражение как сложную функцию, имея ввиду, что y - это функция от x.
 Отсюда видно, что искомая производная равна
Отсюда видно, что искомая производная равна 
Производные основных элементарных функций ( y=x2; y=x3; y=sinx; y=cosx; y=tgx; y=ctgx; y=ex; y=lnx; y=1/x; y=√x - вывод). Таблица производных
Производные простых функций
Вывод
-
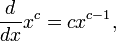 когда
когда  и
и 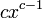 определены,
определены, 
Вывод
Вывод
Таблица производных
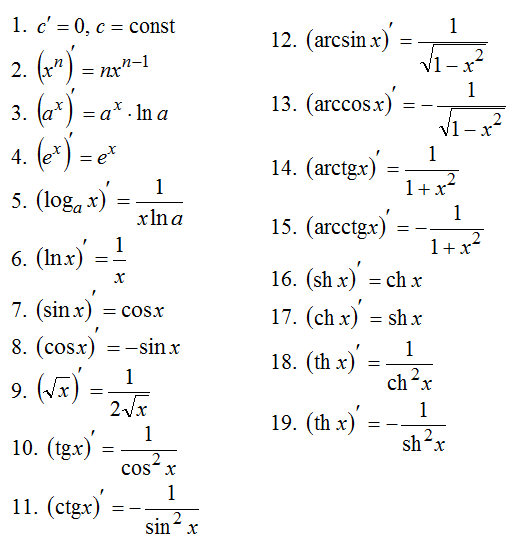
Дифференциал функции y=f(x). Геометрический смысл. Свойства дифференциала
Пусть функция y = f(x) дифференцируема при некотором значении переменной x. Следовательно, в точке x существует конечная производная
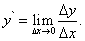
Тогда по определению предела функции разность
 (1)
(1)
является бесконечно малой величиной при 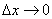 . Выразив из равенства (1) приращение функции, получим
. Выразив из равенства (1) приращение функции, получим
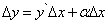 (2)
(2)
(величина 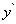 не зависит от
не зависит от  , т. е. остаётся постоянной при
, т. е. остаётся постоянной при 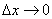 ).
).
Если 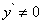 , то в правой части равенства (2) первое слагаемое
, то в правой части равенства (2) первое слагаемое 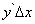 линейно относительно
линейно относительно  . Поэтому при
. Поэтому при
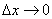
оно является бесконечно малой того же порядка малости, что и  . Второе слагаемое
. Второе слагаемое 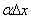 - бесконечно малая более высокого порядка малости, чем первое, так как их отношение
- бесконечно малая более высокого порядка малости, чем первое, так как их отношение 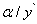 стремится к нулю при
стремится к нулю при
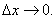
Поэтому говорят, что первое слагаемое формулы (2) является главной, линейной относительно  частью приращения функции; чем меньше
частью приращения функции; чем меньше  , тем большую долю приращения составляет эта часть. Поэтому при малых значениях
, тем большую долю приращения составляет эта часть. Поэтому при малых значениях  (и при
(и при 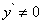 ) приращение функции можно приближенно заменить его главной частью
) приращение функции можно приближенно заменить его главной частью 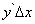 , т.е.
, т.е.
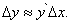 (3)
(3)
Эту главную часть приращения функции называют дифференциалом данной функции в точке xи обозначают
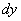
или

Следовательно,
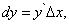 (4)
(4)
или
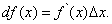 (5)
(5)
Итак, дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной.
Замечание. Нужно помнить, что если x – исходное значение аргумента,

- наращенное значение, то производная в выражении дифференциала берётся в исходной точке x; в формуле (5) это видно из записи, в формуле (4) – нет.
Дифференциал функции можно записать в другой форме:
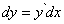 (6)
(6)
или
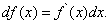
Геометрический смысл дифференциала. Дифференциал функции y = f(x) равен приращению ординаты касательной, проведённой к графику этой функции в точке (x; y), при изменении x на величину 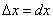 .
.
Дата добавления: 2015-04-18; просмотров: 604; Мы поможем в написании вашей работы!; Нарушение авторских прав |