
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Ый замечательный предел (0/0) и его следствия
Первый замечательный предел имеет вид: 
На практике чаще встречаются модификации первого замечательного предела в виде

где, k – коэффициент.
Пояснение:

Следствия первого замечательного предела:
1. 
2. 
Эти следствия очень просто доказываются, если использовать правило Лопиталя или заменуэквивалентных бесконечно малых функций.
Ой замечательный предел (1∞) и его следствия
Непрерывность функции в точке. Определения
Пусть функция f(x) определена в некоторой окрестности O(x0) точки x0(включая саму точку x0).
Функция f(x) называется непрерывной в точке x0, если существует limx → x0 f(x) , равный значению функции f(x) в этой точке:  т.е.
т.е.
 O( f(x0) ) O( f(x0) )  O(x0) : x O(x0) : x 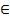 O(x0) O(x0)  f(x) f(x) 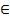 O( f(x0) ) . O( f(x0) ) .
|
Замечание. Равенство  можно записать в виде:
можно записать в виде: 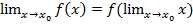
т.е. под знаком непрерывной функции можно переходить к пределу.
Дата добавления: 2015-04-18; просмотров: 367; Мы поможем в написании вашей работы!; Нарушение авторских прав |