Геометрический смысл конечного и бесконечного предела последовательности

Выясним геометрический смысл понятия предела последовательности. Расположим члены последовательности x₁,x₂,..., x_n,... на числовой прямой. Неравенство |x_n-A|<e равносильно следующему A- e < x_n < A + e, которое говорит о том, что члены последовательности x_n попадают в e - окрестность точки A. Вне этой e -окрестности может быть лишь конечное число членов данной последовательности

Ограниченная, бесконечно большая, бесконечно малая, сходящаяся, расходящаяся, монотонно возрастающая, монотонно убывающая последовательности (определения, примеры)

Последовательность называется ограниченной сверху, если существует такое число , что для любого номера ,

Последовательность называется ограниченной снизу, если существует такое число , что для любого номера ,

Последовательность называется ограниченной, если она ограниченная сверху и ограниченная снизу, то есть существует такое число , что для любого номера , Последовательность называется неограниченной, если существует такое число , что существует такой номер , что

Определение (бесконечно большая последовательность). xn – бесконечно большая последовательность, если c>0 N: n>N |x_n|>c.

Пример 1. Последовательности n, 2ⁿ являются бесконечно большими.

Определение (бесконечно малая последовательность). Бесконечно малая последовательность — последовательность, предел которой равен 0.

Пример . Последовательность xn = 1/n является бесконечно малой последовательностью.

Последовательность называется сходящейся, если у нее существует конечный предел (т.е. существует ).

Числовая последовательность {x_n} называется расходящейся, если она не имеет конечного предела, т.е. если она либо имеет бесконечный предел, либо у нее вообще нет предела. В частности всякая неограниченная числовая последовательность расходится.

Если числовая последовательность содержит две или более двух подпоследовательностей, сходящихся к различным пределам, она расходится.

Последовательность элементов множества 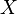называется возрастающей, если каждый следующий элемент этой последовательности превышает предыдущий. Пример(1,2,3…).

Последовательность элементов множества 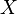называется убывающей, если каждый элемент этой последовательности превышает следующий за ним. Пример(-1,-2,-3..).