Необходимое условие существования производной

Если функция имеет в определенной точке производную, то существует касательная к графику этой функции в этой точке, причем угловой коэффициент этой касательной равен значению производной.

Теорема (необходимое условие существования производной функции в точке). Если функция y = f(x) имеет производную в точке , то функция f(x) в этой точке непрерывна.

Доказательство

Пусть существует . Тогда 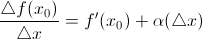, где – бесконечно малая при . ⇒ ;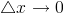

⇒

.

Но это означает, что функция f(x) непрерывна в точке (по геометрическому определению непрерывности).

Замечание. Непрерывность функции в точке не является достаточным условием существования производной этой функции в точке . Например, функция y = |x| непрерывна, но не имеет производной в точке .

Очевидно, что соответствие является функцией, определенной на некотором множестве . Ее называют производной функцииy = f(x) и обозначают

.

Операцию нахождения для функции f(x) ее производной функции называют дифференцированием функции y = f(x).

Основные правила дифференцирования (±, (uv)’, (u/v)’)

Пусть функции и имеют производные в точке . Тогда

1. Константу можно выносить за знак производной.

Пример

2. Производная суммы/разности.

Производная суммы/разности двух функций равна сумме/разности производных от каждой из функций.

Пример

3. Производная произведения.

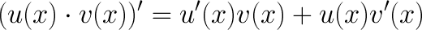
Пример

4. Производная частного.

Пример

5. Производная сложной функции.

Производная сложной функции равна производной этой функции по промежуточному аргументу , умноженной на производную от промежуточного аргумента по основному аргументу .

и и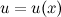меют производные соответственно в точках и . Тогда