Теорема о среднем (Ролля, Лагранжа, Коши). Формулировка, геометрический смысл, следствия

Знание производной некоторой функции позволяет судить о характерных особенностях в поведении этой функции. В основе всех таких исследований лежат некоторые простые теоремы, называемые теоремами о среднем в дифференциальном исчислении.

Начнем рассмотрение таких теорем с теоремы, связываемой с именем французского математика Ролля (1652–1719).

Теорема 1.1. Если функция непрерывна на отрезке 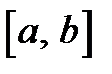, дифференцируема во всех его внутренних точках, а на концах отрезка 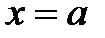, 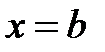обращается в ноль, то существует, по крайней мере, одна точка 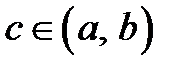, в которой .

Доказательство. Так как функция непрерывна на отрезке , то, согласно свойству 11.1.1, она должна достигать хотя бы один раз на этом отрезке своего минимума и максимума 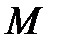(рис. 1.1).

Если , функция постоянна, то есть 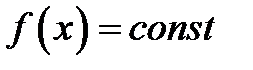. Но в этом случае 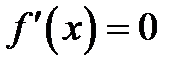для любого .

В общем случае , и хотя бы одно из этих чисел не равно нулю. Предположим для определенности, что . Тогда существует точка 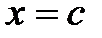, в которой .

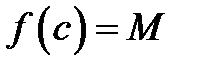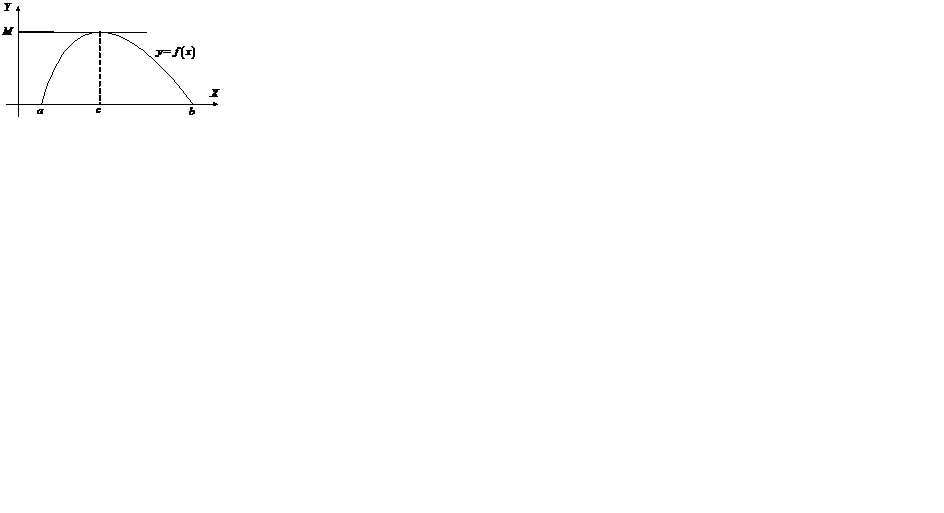
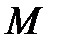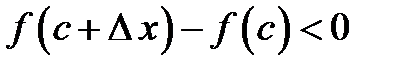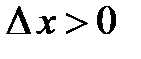Так как рассматриваемое значение является максимальным, то для него справедливо, что для и .

Рассмотрим пределы

для

и

для .

Так как оба предела равны производной функции 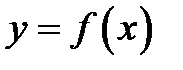в одной и той же точке , то они равны между собой. Значит, из одновременности и следует, что , что и требовалось доказать.

Следует отметить, что данная теорема справедлива и в том случае, когда на концах отрезка функция не обращается в ноль, но принимает равные значения 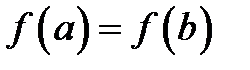. Доказательство проводится аналогично.

Геометрический смысл данной теоремы следующий: если непрерывная кривая пересекает ось 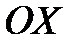в двух точках , или принимает в них равные значения, то, по крайней мере, в одной точке между и касательная к кривой параллельна оси .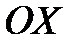

Необходимо отметить, что если не во всех точках у рассматриваемой функции существует производная, то теорема может не выполняться. Это касается, например, функции 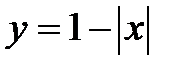(рис. 1.2):

Данная функция непрерывна на отрезке и обращается в ноль на его концах, но ни в одной точке внутри отрезка производная не равна нулю.