Дифференцирование функций, заданных неявно

Пусть значения переменных х и у связаны уравнением

F(x, y) = 0. (1)

Если функция y = f(x), определенная на некотором интервале (а,в), такая, что уравнение (1) при подстановке в него вместо у выражения f(x) обращается в тождество, то говорят, что уравнение (1) задает функцию y = f(x) неявно или что функция y = f(x) есть неявная функция.

Укажем правило нахождения производной неявной функции, не преобразовывая ее в явную, то есть не представляя в виде y = f(x), так как часто это преобразование бывает технически сложным или невозможным.

Для нахождения производной у'_х неявной функции, нужно продифференцировать по х обе части равенства (1), учитывая, что у есть функция от х. Затем из полученного равенства выразить у'_х.

Пример 1. Вычислить у'_х.

У⁵+ху-х² = 0

Продифференцируем обе части по х. Получим 5у⁴у'+у+ху'-2х=0. Выразим у'. y'(5у⁴+х) = 2х-у, у' =(2х-у)/(5у⁴+х).

Пример 2.

tg(x+y) = xy

Продифференцируем обе части по х. Получим или 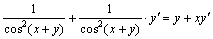. Отсюда 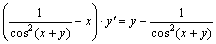или 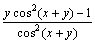. Окончательно .

Заметим, что производная неявной функции выражается через х и у, то есть получается равенство

y' = g(x, y) (2)

Для вычисления второй производной неявной функции, нужно продифференцировать обе части равенства (2) по х и затем подставить выражение g(x, y) вместо y'.

Аналогично можно вычислить производные любого порядка неявной функции.