Режимы движения жидкости. Число Рейнольдса. В зависимости от рода жидкости, скорости ее движения и характера стенок, ограничивающих поток, различают два основных режима движения: ламинарный и

В зависимости от рода жидкости, скорости ее движения и характера стенок, ограничивающих поток, различают два основных режима движения: ламинарный и турбулентный. Ламинарным называют упорядоченное движение, когда отдельные слои скользят друг по другу, не перемешиваясь (рис. ).

Ламинарный режим движения можно наблюдать чаще у вязких жидкостей, таких как нефть, масла и т. п.

Турбулентным называют режим, при котором наблюдается беспорядочное движение, когда частицы жидкости движутся по сложным траекториям и слои жидкости постоянно перемешиваются друг с другом (рис. 3.8).

Рис. 3.8. Режимы течения

Опыты показали, что переход от турбулентного режима к ламинарному происходит при определенной скорости (эта скорость называется критической),которая различна для разных жидкостей и диаметров труб; при этом критическая скорость растет с увеличением вязкости жидкости и с уменьшением диаметра труб.

Рейнольдсом и рядом других ученых опытным путем было установлено, что признаком режима движения является некоторое безразмерное число, учитывающее основные характеристики потока

, (3.8)

где υ – скорость, м/сек; R - гидравлический радиус, м; v - кинематический коэффициент вязкости, м²/сек.

Это отношение называется числом Рейнолъдса. Значение числа Re, при котором турбулентный режим переходит в ламинарный, называют критическим числом Рейнолъдса Re_Kp.

Если фактическое значение числа Re, вычисленного по формуле (3.8), будет больше критического Rе > Rе_Kp – режим движения турбулентный, когда Rе < Rе_Kp – режим ламинарный.

Для напорного движения в цилиндрических трубах удобнее число Рейнольдса определять по отношению к диаметру d, т. е.

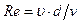, (3.9)

где d – диаметр трубы.

В этом случае Rе_Kp получается равным ~ 2320. Если в формуле () для трубопроводов круглого сечения d выразить через гидравлический радиус ,то получим Rе_Kp=575. Для других трубопроводов и каналов некруглых сечений можно принимать значение критического числа Рейнольдса Rе_Kp = 300 (при вычислении Rе через гидравлический радиус).