при постоянном напоре

Рассмотрим большой резервуар с жидкостью под давлением Р₀, имеющий малое круглое отверстие в стенке на достаточно большой глубине Н₀ от свободной поверхности (рис.3.22).

Рис. 3.22. Истечение из резервуара через малое отверстие

Жидкость вытекает в воздушное пространство с давлением Р₁. Пусть отверстие имеет форму, показанную на рис.3.23, а, т.е. выполнено в виде сверления в тонкой стенке без обработки входной кромки или имеет форму, показанную на рис.3.23, б, т.е. выполнено в толстой стенке, но с заострением входной кромки с внешней стороны. Струя, отрываясь от кромки отверстия, несколько сжимается (рис.3.23, а). Такое сжатие обусловлено движением жидкости от различных направлений, в том числе и от радиального движения по стенке, к осевому движению в струе.

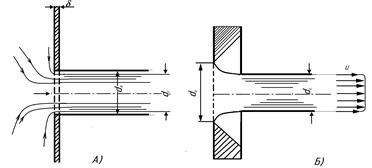
Рис. 3.23. Истечение через круглое отверстие

Степень сжатия оценивается коэффициентом сжатия.

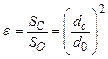
где S_с и S_о - площади поперечного сечения струи и отверстия соответственно; d_с и d_о - диаметры струи и отверстия соответственно.

Скорость истечения жидкости через отверстие такое отверстие

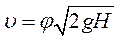(3.20)

где Н - напор жидкости, определяется как

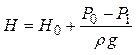
φ- коэффициент скорости

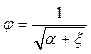
где α - коэффициент Кориолиса; ζ- коэффициент сопротивления отверстия.

Расход жидкости определяется как произведение действительной скорости истечения на фактическую площадь сечения:

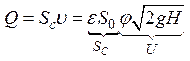
Произведение ε и φ принято обозначать буквой и называть коэффициентом расхода, т.е. μ = εφ.

В итоге получаем расход

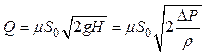(3.21)

где ΔР - расчетная разность давлений, под действием которой происходит истечение.

При помощи этого выражения решается основная задача - определяется расход.