Потери напора при турбулентном движении. Первая область - область малых Re и Δ/r0, где коэффициент λ не зависит от шероховатости, а определяется лишь числом Re (отмечена на рис.3.12 прямой

Первая область - область малых Re и Δ/r₀, где коэффициент λ не зависит от шероховатости, а определяется лишь числом Re (отмечена на рис.3.12 прямой II ). Это область гидравлически гладких труб. Если число Рейнольдса лежит в диапазоне 4000 < Re < 10(d/Δ_э) коэффициент λ определяется по полуэмпирической формуле Блазиуса

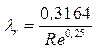(3.14)

Во второй области, расположенной между линий II и пунктирной линией справа, коэффициент λ зависит одновременно от двух параметров - числа Re и относительной шероховатости Δ/r₀, которую можно заменить на Δ_э. Для определения коэффициента λ в этой области может служить универсальная формула А.Д. Альтшуля:

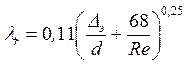(3.15)

где Δ_э – эквивалентная абсолютная шероховатость.

Третья область – область больших Re и Δ/r₀, где коэффициент λ не зависит от числа Re, а определяется лишь относительной шероховатостью (область расположена справа от пунктирной линии). Это область шероховатых труб, в которой все линии с различными шероховатостями параллельны между собой. Эту область называют областью автомодельности или режимом квадратичного сопротивления, т.к. здесь гидравлические потери пропорциональны квадрату скорости.

Определение λ для этой области производят по упрощенной формуле Альтшуля:

. (3.16)

Итак, потери напора, определяемые по формуле Дарси-Вейсбаха, можно определить, зная коэффициент гидравлического сопротивления, который определяется в зависимости от числа Рейнольдса Re и от эквивалентной абсолютной шероховатости Δ_э.