Вопрос 5.Оптические резонаторы. Свойства плоского резонатора. Потери в оптических резонаторах.

Резонаторы Важнейшим элементом квантовых генераторов радио- и оптического диапазонов является резонатор. За счет многократного отражения в резонаторе достигается наиболее полное взаимодействие электромагнитного излучения с активной средой. Обеспечивая положительную обратную связь, резонатор существенно влияет на свойства генерируемого активной средой излучения, определяя, в частности, его диаграмму направленности и спектральный состав. В широком смысле резонатором называют колебательную систему, в которой возможно накопление энергии акустических, механических или электромагнитных колебаний. Простейшим электромагнитным резонатором, применяемым в радиодиапазоне до частот несколько десятков мегагерц, является колебательный контур. С увеличением частоты размеры контура становятся соизмеримыми с длиной волны, что приводит к резкому возрастанию излучения из контура, и он теряет свои резонансные свойства. Поэтому в СВЧ-радиодиапазоне при частотах порядка 10⁹...10¹¹ Гц (λ ≈ 0.3...30 см) применяют объемный резонатор — колебательную систему, представляющую собой полость с проводящими стенками, внутри которой могут возбуждаться электромагнитные колебания. В объемном резонаторе могут возбуждаться колебания только определенных длин волн и определенной структуры, образующие стоячую волну. Частоты этих колебаний называются резонансными или собственными частотами резонатора, а колебания — собственными колебаниями резонатора или модами. Таким образом мода — это собственный тип колебаний резонатора. По более точному определению, мода резонатора представляет собой стационарную конфигурацию электромагнитного поля, которая удовлетворяет уравнениям Максвелла и граничным условиям. Электрическое поле такой конфигурации можно записать в виде

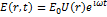(2.23)

Где ω ­ собственная частота резонатора Например, для объемного резонатора, представляющего собой прямоугольный параллелепипед с размерами ребер L₁, L₂ и L₃, длины волн собственных типов колебаний λ_mnq находят из соотношения

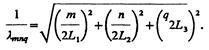(2.24)

Здесь m, n и q — целые числа, определяющие число полуволн, укладывающихся вдоль сторон L₁ L₂ и L₃.

Соотношение (2.24) выражает условие образования стоячей волны при её отражениях от стенок резонатора. Например, для m=n = 0 имеем 1/λ_00q = q/2L₃, или L₃ = 0.5λq. На длине L₃ укладывается целое число полуволн, т. е. образуется стоячая волна.

Очевидно, собственные частоты объемного резонатора определяются только его геометрией (в случае незаполненных резонаторов). Отличительной особенностью объемных резонаторов является то, что их размеры соизмеримы с длиной волны. Поэтому число собственных типов колебаний в таком резонаторе мало, а собственные частоты разнесены далеко друг от друга по спектру. Изменяя размеры резонатора, можно изменять (перестраивать) его резонансные частоты. Электромагнитные волны, распространяющиеся в свободном пространстве, являются поперечными, и векторы Е, Н, к взаимно перпендикулярны. Электромагнитные колебания в объемном резонаторе не являются поперечными: один из векторов Е или Н имеет проекцию на направление распространения волны — продольную составляющую. Если продольную составляющую имеет вектор Е, то электромагнитное колебание называют электрическим и обозначают Е или ТМ. Если продольную составляющую имеет вектор Н, то колебание называют магнитным и обозначают Н или ТЕ. Каждое колебание, например, в прямоугольном резонаторе характеризуют тремя индексами m, n и q (2.24), соответствующими числу полуволн в направлениях x, y и z. Для цилиндрического объемного резонатора, часто применяемого в СВЧ-диапазоне, индексы m, n и q указывают число полуволн по диаметру, окружности и длине резонатора.

Колебания в объемном резонаторе (который является замкнутым со всех сторон) возбуждают с помощью петлеобразного проводника — петли связи или через специальное отверстие (щель). Аналогично обеспечивается вывод электромагнитной энергии наружу.

Кроме собственных частот и собственных типов колебаний объемный резонатор, как и любой другой резонатор, характеризуется потерями энергии (например, тепловыми потерями и потерями на излучение в окружающее пространство). Это свойство резонатора характеризует добротность. Добротность резонатора Q есть отношение энергии, запасенной в резонаторе, к средней энергии, теряемой за 1/2π часть периода колебаний. Добротность объемных резонаторов в СВЧ-диапазоне имеет порядок 10³.

При переходе от радиочастот СВЧ-диапазона к оптическим частотам объемные резонаторы начинают терять свои резонансные свойства: при уменьшении длины волны и неизменных размерах резонатора спектр собственных частот сгущается, так что различные типы колебаний накладываются друг на друга и селективные свойства резонатора исчезают.

Для того чтобы разрядить спектр собственных частот, в оптическом диапазоне вместо объемных резонаторов применяют открытые резонаторы. Открытым резонатором называют объемный резонатор, отражающие стенки которого не замкнуты. Резонансными свойствами обладают открытые резонаторы только вполне определенной геометрической конфигурации. Открытый резонатор для оптического диапазона называют оптическим резонатором.

Простейший оптический резонатор образуют два плоских зеркала, расположенные строго параллельно друг другу (рис. 2.10). Такой плоский резонатор, очевидно, можно рассматривать как открытый резонатор, образованный из прямоугольного объемного резонатора, четыре боковые стенки которого удалены. Прямая 00', проходящая через центры зеркал перпендикулярно их поверхностям, называется оптической осью резонатора. Электромагнитные волны, распространяющиеся вдоль оптической оси, будут отражаться от зеркал и интерферировать между собой. Те из них, для которых выполняется условие резонанса qλ/2=L, будут интерферировать на максимум, образуя в резонаторе стоячую волну, как показано на рис. 2.10. За счет многократного прохождения таких волн резко увеличивается эффективность их взаимодействия с рабочим веществом, помещаемым в резонатор. Волны, распространяющиеся под углом (не слишком малым) к оптической оси, после нескольких отражений выходят из резонатора. Этим и достигается разрежение спектра собственных частот открытого резонатора по сравнению с объемным.

Колебания, распространяющиеся строго вдоль оптической оси резонатора, обладают наивысшей добротностью и называются аксиальными колебаниями. Определим расстояние Д v между соседними аксиальными колебаниями при Я= 1 мхм для резонатора длиной 1 м. На этой длине будет укладываться 2-106 полуволн (q=2·10⁶). Расстояние между ближайшими типами колебаний

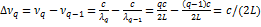(2.26)

Для L=l м получаем 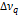=150 МГц, а для L=l см 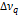=l,5·10¹⁰ Гц (вместо 10 Гц для объемного резонатора с L= 1 см).

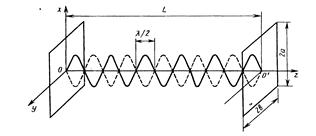
Рисунок 2.10 Схема оптического резонатора с плоскими прямоугольными зеркалами (интерферометр Фабри—Перо)

Несмотря на столь существенное разрежение спектра собственных частот, частотный интервал между соседними типами колебаний в оптических резонаторах с размерами L≈0,1...2 м значительно меньше ширины спектральной линии даже в газах, где ее ширина минимальна по сравнению с другими веществами. Это означает, что в пределах спектральной линии активной лазерной среды обычно укладывается много (от десятков до десятков тысяч) собственных типов колебаний резонатора (рис. 2.11). Поэтому такой резонатор называется многомодовым или многочастотным. При этом добротность оптического резонатора существенно выше добротности спектральной линии. Спектр собственных частот в системе (активное вещество + резонатор) в оптическом диапазоне (в лазерах), как видно из рис. 2.11, будет определяться собственными частотами резонатора, лежащими вблизи максимума спектральной линии.

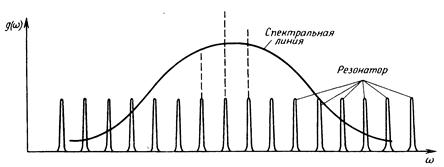
Рисунок 2.11 Сравнение формы спектральной линии со спектром собственных частот оптического резонатора. Пунктирными линиями обозначены частоты, наиболее благоприятные для развития генерации.

Для определения свойств оптического резонатора в общем случае надо записать уравнения Максвелла и решить их с учетом соответствующих граничных условий. Если проследить за первоначальной волной, претерпевающей многократные отражения, то можно убедиться, что в конце концов в резонаторе устанавливается некоторое стационарное состояние электромагнитного поля. Оно характеризуется тем, что при дальнейших отражениях (после нескольких сотен отражений) установившееся распределение электромагнитного поля не изменяется. Такое стационарное распределение поля и определяет собственные колебания резонатора. Эти колебания, имеющие пренебрежимо малые проекции Е и Н на ось z, называются трансверсальными электромагнитными колебаниями и обозначаются ТЕМ_mnq. Смысл индексов m, n и q тот же, что в объемных резонаторах.

Величина q, указывающая число полуволн, укладывающихся на длине L резонатора, в оптическом диапазоне очень велика, и при обозначении типов колебаний ее обычно опускают; m и n, наоборот, малы. Для аксиальных колебаний m=n=0 и их обозначают ТЕМ₀₀. Кроме ТЕМ₀₀-колебаний возможны ТЕМ₁₀ ТЕМ₂₀, ТЕМ₀₂, ТЕМ₁₁-колебания и т. д., которые называются неаксиальными колебаниями. Казалось бы, неаксиальные моды должны быстро выходить из резонатора, поскольку они распространяются не строго параллельно его оптической оси. На самом деле из-за явлений дифракции на краях зеркал неаксиальные колебания, дойдя до края зеркала, будут отражаться внутри резонатора. Это явление аналогично отражению электромагнитной волны от границы волновода, если угол к нормали мал, то коэффициент отражения близок единице. Важно, что волны, распространяющиеся под малыми углами θ к оси резонатора (неаксиальные моды с малыми индексами m и n), как и аксиальные ТЕМ₀₀-моды, будут обладать высокими добротностями. С увеличением m и n дифракционные потери будут увеличиваться, а добротность — падать.

Под добротностью оптического резонатора, как и других колебательных систем, понимают величину

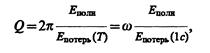(2.27)

где Е_полн — полная энергия, запасенная в резонаторе; 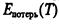— энергия, теряемая за период; — энергия, теряемая за 1 с.

Добротность определяется потерями в резонаторе. Из (2.27) получаем, что изменение энергии Е_ω, запасенной в моде частотой 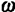за время dt,

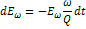
Отсюда следует, что запасенная в резонаторе энергия вследствие потерь будет уменьшаться по экспоненциальному закону

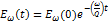(2.28)

т. е. аналогично изменению во времени мощности излучения затухания моды резонатора

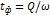
которая называется также временем жизни фотона. Наряду с добротностью эту величину используют для характеристики потерь в резонаторе.

Для вывода излучения наружу одно из зеркал резонатора должно быть частично пропускающим (полупрозрачным). Это определяет необходимые полезные потери резонатора, называемые потерями на излучение. Пусть коэффициент отражения зеркала, через которое выводится излучение, равен R. Тогда коэффициент пропускания этого зеркала T=(1– R) (потери в современных многослойных диэлектрических зеркалах малы и ими можно пренебречь). Если длина резонатора L»λ, то теряемая за единицу времени энергия равна Е_ω(1—R)c/(2L). Из (2.27) получаем добротность резонатора, определяемую потерями на излучение

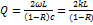(2.29)

где k=2π/λ. Взяв типичные значения λ=1 мкм, L=1 м и R=0,9, получаем Q≈ 1 · 10⁸.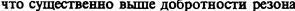

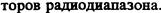
Кроме необходимых потерь на излучение в реальных резонаторах существуют дополнительные потери. Перечислим основные из них.

1. Дифракционные потери. Эти потери связаны с дифракцией электромагнитной волны на зеркалах резонатора, имеющих конечные размеры. Дифракционные потери определяются отношением a²/(λL). Чем меньше поперечные размеры а зеркала, тем больше дифракционные потери. Дифракционные потери зависят также от типа колебаний. Они минимальны для аксиальных ТЕМ₀₀-мод и возрастают с увеличением индексов m и n моды. Это используют для селекции неаксиальных мод в резонаторах.

2. Потери на несовершенствах зеркал. Эти потери обусловлены возможным поглощением в зеркалах (что недопустимо), рассеянием на шероховатостях, отклонением геометрии зеркала от заданной и т. д. Для их исключения к зеркалам резонатора предъявляются исключительно высокие требования. В частности, обработка поверхности зеркала должна проводиться с погрешностью ~ 0.1λ.

3. Потери на разъюстировку резонатора. Для того чтобы система из двух зеркал обладала резонансными свойствами, необходима очень точная их ориентация относительно друг друга. В частности, в плоском резонаторе отражающие поверхности двух плоских зеркал должны быть строго параллельны друг другу. Для выполнения этого требования зеркала резонатора очень точно настраивают (юстируют). Угол между плоскостями зеркал, называемый углом разъюстировки, в плоском резонаторе не должен превышать нескольких угловых секунд.

4. Потери в активном веществе. Они обусловлены поглощением и рассеянием энергии на различных дефектах в активной среде, заполняющей резонатор.