Билет 15, 1?

Возбуждение активного вещества (накачка)

Усиление электромагнитных колебаний с помощью вынужденного излучения возможно лишь в среде с инверсией населенностей энергетических уровней. Такое состояние активного вещества достигается в термодинамически неравновесных системах с помощью накачки. Накачку можно осуществлять различными методами. Перечислим наиболее распространенные из них.

1. Накачка вспомогательным излучением (оптическая накачка). Этот метод является наиболее универсальным и широко используется для накачки твердотельных лазеров на диэлектриках, жидкостных лазеров, может применяться в полупроводниковых и газовых лазерах. Сущность метода состоит в том, что активное вещество облучают мощным электромагнитным излучением называемым вспомогательным излучением или излучением накачки. Это излучение выбирают так, чтобы оно поглощалось активным веществом, переводя активные центры из основного в возбужденное состояние. В качестве источников накачки в оптическом диапазоне могут служить разнообразные источники света, в том числе обычные лампы накаливания, специальные мощные ксеноновые лампы-вспышки, ртутные лампы, полупроводниковые светодиоды, солнечное излучение и др. В СВЧ-диапазоне источниками накачки могут быть генераторы СВЧ-колебаний, например клистронные или магнетронные генераторы.

2. Накачка с помощью газового разряда. Этот метод применяется в газоразрядных лазерах, где возбуждение активных атомов и молекул осуществляется за счет неупругих столкновений, приводящих к обмену энергией частиц (свободных электронов, атомов, молекул, ионов) в облаке газового разряда.

3. Сортировка частиц. Данный метод используется в приборах СВЧ-диапазона — так называемых пучковых мазерах. Молекулы рабочего вещества, находящиеся в термодинамическом равновесии в основном и возбужденном состояниях ((Е₂ – Е₁) « kТ), пространственно разделяют так, чтобы в рабочий объем попадали только возбужденные молекулы. Невозбужденные молекулы выводятся из рабочего пучка. Такое разделение возможно вследствие того, что некоторые молекулы,

находящиеся в основном и возбужденном состояниях, по-разному реагируют с внешними электрическим и магнитным полями.

4. Инжекция неосновных носителей заряда через р-n-переход. Этот метод применяется в полупроводниковых инжекционных лазерах и позволяет непосредственно, без промежуточных процессов, преобразовывать электрическую энергию источника в когерентное электромагнитное излучение лазера.

5. Возбуждение частицами высоких энергий, например ускоренными электронами. Такой метод используется в полупроводниковых лазерах с электронной накачкой, а также может применяться в других типах лазеров. Пучок предварительно ускоренных электронов (β-частиц) направляется на рабочую мишень из активного вещества, вызывая возбуждение и ионизацию активных центров.

6. Химическая накачка. Данный метод применяется в газовых лазерах. Используется ряд химических реакций, протекающих между газообразными веществами, в результате которых конечный продукт реакции оказывается в возбужденном состоянии.

7. Газодинамическая накачка. Этот метод применяется в газовых лазерах и сводится к тому, что рабочий газ, нагретый до высокой температуры, резко охлаждается. Переходя в равновесное состояние, частицы (молекулы) газа задерживаются в наиболее долгоживущих (метастабильных) состояниях, в результате чего может быть достигнута инверсия населенностей.

15.2 Квазиравновесный режим водородного восстановления кремния из тетрахлорида кремния

4.2.1. Равновесный выход конденсирующегося кремния

Процесс водородного восстановления элементов из их галогенидов (чаще всего хлоридов) широко используют в электронной промышленности для получения эпитаксиальных слоёв кремния и германия, поликристаллического кремния и целого ряда других элементов высокой степени чистоты. Далее мы будем рассматривать только процесс водородного восстановления кремния из его тетрахлорида.

Важнейшим показателем эффективности такого технологического процесса является равновесный выход конденсированного кремния β. Пусть в зоне протекания процесса водородного восстановления к состоянию термодинамического равновесия приходит некоторое количество исходной парогазовой смеси. По определению β есть отношение изменение числа атомов кремния в конденсированной фазе в результате установления термодинамического равновесия в зоне реакции ∆n_Si,¥^(к) к числу n_Si,0 ^(п) атомов кремния в выделенном количестве исходной смеси.

(4.2.1)

Везде далее величины, относящиеся к состоянию равновесия, будем снабжать индексом «∞», а относящиеся к исходному состоянию – индексом «0». Ясно, что ∆n_Si,¥^(к) равно убыли количества атомов кремния в парогазовой фазе в результате установления термодинамического равновесия

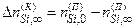. (4.2.2)

Поэтому

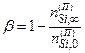. (4.2.3)

Число атомов восстанавливаемого элемента в выделенном количестве исходной парогазовой смеси удобно выразить через число атомов галогена – неконденсирующегося элемента, для которого количество атомов в парогазовой фазе остаётся неизменным в ходе процесса. Так как исходным кремнийсодержащим веществом является SiCl₄, то

, (4.2.4)

где учтено, что для неконденсирующегося хлора . В соответствии с (4.2.3) и (4.2.4) находим

(4.2.5)

Если для равновесной парогазовой смеси ξ < 0.25, то происходит осаждение кремния (β > 0); если же ξ > 0.25, то происходит травление кремния, находящегося в осадке, тетрахлоридом кремния.

Величина , входящая в (4.2.5), может быть выражена через отношение гипотетических давлений атомов кремния и хлора в состоянии равновесия

. (4.2.6)

По определению гипотетическим давлением атомов i-го сорта называют такое давление, которое имел бы при данной температуре идеальный газ, содержащий в единице объёма столько же частиц, сколько содержится атомов i-го сорта в единице объёма данной парогазовой смеси. Если поведение всех компонент парогазовой фазы близко к идеальногазовому, что мы и будем предполагать в дальнейшем, то гипотетическое давление является удобной мерой содержания атомов элемента в единице объёма смеси. В самом деле, в соответствии с уравнением Менделеева- Клапейрона объёмная концентрация молекул j-го компонента смеси N_j^(П) равна

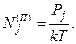(4.2.7)

Здесь Р_j-парциальное давление j-го компонента; k-постоянная Больцмана; Т - абсолютная температура. Пусть -число атомов i-го сорта в компоненте j. Тогда в соответствии с определением гипотетического давления и формулой (4.2.7), используя химический символ элемента вместо индекса i, можно записать следующее выражение для ξ

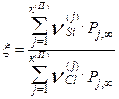. (4.2.8)

Суммирование в (4.2.8) проводится по всем к^(П) компонентам парогазовой фазы. Отметим, что Р^ГИП_Cl,∞ = P^ГИП_Cl,0 = 4P^ГИП_SiCl4,0, поскольку атомы хлора не конденсируются, а исходным кремнийсодержащим компонентом по условию является тетрахлорид кремния. Соотношение (4.2.8) целесообразно записать в более наглядном виде, используя обобщённое выражение вида Si_nH_mCl_l для химической формулы газообразных компонент в системе Si-H-Cl

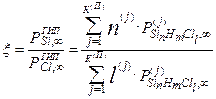. (4.2.9)

Подставив выражение (4.2.9) в (4.2.5), получаем окончательное выражение для расчёта равновесного выхода кремния в процессе его водородного восстановления из тетрахлорида

. (4.2.10)

Формула (4.2.10) показывает, что для определения равновесного выхода кремния необходимо рассчитать равновесные парциальные давления компонент парогазовой фазы в зоне протекания процесса водородного восстановления.

Далее нам предстоит провести упрощённый термодинамический анализ системы Si – H – Cl для высокотемпературной области с целью определения зависимости равновесных парциальных давлений компонент парогазовой фазы и равновесного выхода кремния от температуры и состава исходной смеси.

4.2.2. Компонентный состав и базисные реакции в системе

Si – H – Cl в области высоких температур

В процессе водородного восстановления, как и во многих других химических процессах, образование целевого продукта сопровождается множеством побочных реакций, приводящих к появлению в системе большого числа различных компонент. Далее мы рассмотрим методику расчёта равновесного состава системы для случая протекания процесса в условиях постоянства температуры и давления.

Термодинамическое рассмотрение начинается с выбора компонент в газовой фазе и в конденсированном состоянии, которые будут учитываться при расчёте. Компонентами или составляющими системы будем называть все те вещества или сорта частиц, которые она включает в состоянии термодинамического равновесия. Указанный выбор проводят на основании имеющихся литературных данных о процессе, а также путём анализа констант равновесия возможных химических реакций в системе. Компоненты, образующиеся при заданных условиях в реакциях с очень малыми константами равновесия, можно не принимать во внимание. При последующем упрощённом термодинамическом анализе химического равновесия в системе Si – H – Cl в интервале температур от 1000К до 1500К и при давлении 1 атм будем учитывать следующие компоненты парогазовой фазы : H₂, HCl, SiCl₂, SiCl₄ и SiCl₃. В конденсированной фазе будем учитывать наличие только твёрдого кремния Si^ТВ. Между указанными компонентами возможно протекание множества химических реакций. Стехиометрическое уравнение каждой такой реакции можно записать в виде в виде

(4.2.11)

где А_i – химические символы участников реакции (реактантов); ν_i - соответствующие стехиометрические коэффициенты. Суммирование проводится по всем компонентам системы, участвующим в рассматриваемой реакции. Договоримся использовать в дальнейшем для каждой отдельной реакции такой набор стехиометрических коэффициентов {ν_i}, где эти коэффициенты у продуктов реакции положительны, а у исходных веществ отрицательны и представляют собой целые числа, не имеющие целочисленного делителя отличного от единицы.

Следующий этап расчёта состоит в определении тех реакций, которые необходимо учитывать. Для каждой многокомпонентной химически реагирующей системы можно указать набор химических реакций, стехиометрические уравнения которых являются линейно независимыми. Их принято называть базисными реакциями. Именно на основе таких реакций можно составить независимые уравнения химического равновесия (см. п. 4.2.3). Число и вид линейно независимых реакций в системе можно установить методами линейной алгебры, используя уравнения баланса атомов элементов, участвующих в процессе. Мы не станем проводить подобный анализ, а воспользуемся лишь его результатами. Как можно убедиться, один и тот же разветвлённый химический процесс может быть представлен разными наборами базисных реакций. Все они являются эквивалентными с точки зрения термодинамики. В последующем анализе системы Si – H – Cl в качестве базисных будут приняты следующие линейно независимые химические реакции:

H₂+SiCl₄=2HCl+SiCl₂; (4.2.12)

2H₂+SiCl₄=4HCl+Si_(ТВ.) , (4.2.13)

H₂+2SiCl₄=2HCl+2SiCl₃ . (4.2.14)

Для удобства физической интерпретации исходные вещества записаны в левых частях уравнений. Очевидным признаком линейной независимости предлагаемого набора стехиометрических уравнений базисных химических реакций является наличие в каждом из них нового компонента, не присутствующего во всех остальных уравнениях. Другой возможный набор базисных реакций мог бы включать реакции атомизации всех учитываемых компонент паровой фазы. При этом уравнение реакции атомизации хотя бы одного кремнийсодержащего компонента должно включать конденсированный кремний. С термодинамической точки зрения такой набор будет эквивалентен набору уравнений (4.2.12)-(4.2.14). Однако численное решение системы уравнений химического равновесия, получаемых на его основе, может оказаться более трудоёмким.

4.2.3. Система уравнений химического равновесия

Мы рассматриваем многофазную систему, в которой возможно одновременное протекание нескольких химических реакций, и хотим найти давления компонент парогазовой фазы в состоянии равновесия. Систему уравнений, из которых можно определить эти давления, принято называть системой уравнений химического равновесия. В соответствии с выбором компонентного состава системы (см. п. 4.2.2), неизвестных давлений пять. Давлением паров атомов кремния в расчёте пренебрегаем. Первые три уравнения системы можно получить, записав выражения для констант равновесия базисных реакций (4.2.12) – (4.2.14)

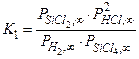; (4.2.15)

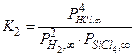; (4.2.16)

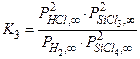. (4.2.17)

Здесь через P_i,∞ обозначены безразмерные отношения равновесных парциальных давлений газообразных компонент к давлению P⁰ , принимаемому за стандартное. В данном случае за стандартное удобно принять давление P⁰ = 1атм. Следовательно, величины P_i,∞ численно равны искомым парциальным давлениям, выраженным в атмосферах.

В качестве четвёртого берём уравнение, выражающее условие постоянства давления Р₀ в системе

(4.2.18)

Будем считать что (5.2.18) приведено к безразмерной форме путём деления на Р⁰ = 1 атм.

Поскольку известно, что атомы хлора и водорода в данной системе не входят в состав конденсированной фазы, то отношение их гипотетических давлений должно оставаться неизменным в ходе процесса. Обозначим отношение Р^гип_Cl/Р^гип_Н =4P_SiCl4,0/2P_H2,0 через 2М и запишем условие материального баланса неконденсирующихся атомов в виде

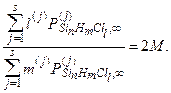(4.2.19)

Будем считать, что и (4.2.19) приведено к безразмерной форме путём деления числителя и знаменателя левой части на Р⁰=1 атм.

В итоге получена система пяти уравнений относительно пяти безразмерных неизвестных P_i, численно равных равновесным парциальным давлениям компонент парогазовой фазы, выраженным в атмосферах. Для её решения необходимы значения констант равновесия базисных химических реакций при температуре процесса водородного восстановления и значение параметра М, задающего состав исходной смеси. При условии, что полное давление в системе Р₀ равно одной атмосфере, правая часть (4.2.18) будет равна единице.

4.2.4. Массовая производительность реактора

в квазиравновесном режиме

Если в зоне протекания процесса водородного восстановления смесь реагирующих компонентов успевает прийти в состояние, мало отличающееся от равновесного, то говорят, что химический реактор работает в квазиравновесном режиме. Для такого режима легко найти массовую производительность реактора Q, зная равновесный выход кремния b и массовый расход J тетрахлорида кремния:

, (4.2.20)

где c - массовая доля кремния в исходном кремнийсодержащем соединении. Для SiCl₄ c = 0.167. Обычно величины Q и J измеряют в килограммах в час.

Билет 16