Билет12, вопрос1

УШИРЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ

При рассмотрении энергетических состояний квантовых систем в нас не интересовал вопрос о ширине дискретных энергетических уровней атомов и молекул, и эти уровни принимались бесконечно узкими. Излучательным переходам между такими идеализированными уровнями энергии соответствовала бы бесконечно узкая спектральная линия излучения (или поглощения) на строго фиксированной частоте.

Распределение интенсивности излучения (или поглощения) по частоте в пределах данной линии характеризуется функцией g(ω), которая называется форм-фактором спектральной линии или просто формой линии. Эта функция нормирована

(1)

Для характеристики относительной ширины спектральной линии используют понятие добротности спектральной линии, которая численно равна отношению резонансной частоты ω₀ в максимуме линии к ее ширине Δω на уровне половинной интенсивности.

В реальных квантовых системах существует ряд факторов, приводящих к уширению их энергетических уровней и соответственно к уширению спектральных линий. Рассмотрим наиболее характерные из них.

Естественное уширение. Это уширение связано с конечностью времени пребывания атомов и молекул в возбужденном состоянии, что, как отмечалось, приводит к «размытию» энергетического уровня на величину порядка δE≈ħ/τ. Отметим, что «естественная ширина линии» определяет тот предел, уже которого спектральная линия в естественных условиях быть не может.

Форма спектральной линии, определяемая конечным временем жизни в возбужденном состоянии, была получена ранее, где было показано, что спектр излучения затухающего осциллятора описывается функцией Лоренца ( 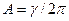, ) или, другими словами, спектральная линия имеет лоренцеву форму. Это выражение перепишем в виде

, (2)

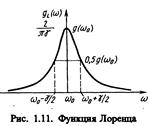где Δω =γ - ширина линии на уровне 0,5 от максимума, а ω₀ — резонансная частота. Если переход осуществляется в основное состояние 0, то Δω=γ=А_m0. Если нижний уровень n неявляется основным, то необходимо учитывать возможность спонтанного распада не только верхнего m, но и нижнего n уровней. В этом случае . Заметим, что чем больше вероятность спонтанного испускания A_m, тем больше естественная ширина спектральной линии.

Типичное значение естественной ширины линии для разрешенных в дипольном приближении переходов в видимой области спектра Δω=А_mn≈10⁸ с^-1, т. е. Δν порядка 20 МГц при ν_o=5*10¹⁴ Гц.

Для переходов с метастабильных уровней естественная ширина линии существенно меньше и при тех же условиях имеет порядок сотен герц.

Так как коэффициент Эйнштейна А_mn~ν³ [ ], то в радиодиапазоне естественная ширина линии существенно меньше, чем в оптическом диапазоне. Например, для газообразного аммиака NH₃ спектральная линия перехода с частотой ν_o = 24870 МГц (λ₀=1,25 см) имеет естественную ширину~ 10^-3Гц.

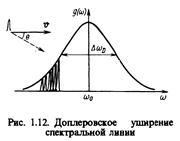Доплеровское упшренне. Эффект Доплера есть изменение частоты (длины волны), наблюдаемое при движении источника волн относительно приемника. Этот эффект вытекает из теории относительности и характерен для любых волн, в том числе для звуковых, электромагнитных и т. д. Если источник излучает электромагнитные волны с собственной частотой ω₀, то длянаблюдателя, относительно которого он движется со скоростью v (рис. 1.12), воспринимаемая частота излучения . (3)

При v « с (с — скорость света)

(4)

Хаотичность теплового движения атомов и молекул в газе приводит к тому, что вместо одной резонансной линии с частотой ω₀ приемник воспринимает совокупность плотно расположенных линий, огибающая которых дает наблюдаемый контур спектральной линии, как показано на рис. Ширина этого спектра пропорциональна наиболее вероятной скорости частиц в газе (т. е. зависит от температуры) и собственной частоте перехода ω₀. Зная распределение частиц по скоростям (распределение Максвелла)

, (5)

где - наиболее вероятная скорость движения частиц в газе, и учитывая выражение 4), можно получить форму спектральной линии, обусловленную доплеровским уширением

. (6)

Здесь

, (7)

— ширина доплеровской линии на уровне 0,5 от максимального значения при ω=ω₀. Подставляя численные значения констант в (7), получаем формулу, удобную для численных расчетов

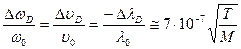, (8)

где М - относительная молекулярная масса, а температура Т выражена в К.

Функция (6) есть функция Гаусса, поэтому говорят, что линия, уширенная за счет эффекта Доплера, имеет гауссову форму.

В условиях газового разряда для легких атомов величина , что для видимой области спектра при ν_o=10¹⁴ Гц дает ГГц. В радиодиапазоне, например, для линии аммиака ν_o=24870 МГц, при комнатной температуре доплеровское уширение , т. е. в миллионы раз превышает естественную ширину линии.

Уширение вследствие столкновений. Столкновения атомов с другими атомами, ионами, свободными электронами или стенками сосуда в газе, а также взаимодействие атомов с решеткой в твердых телах (которое можно рассматривать как столкновение с фононом) приводят к увеличению скорости обмена энергией между частицами и соответственно к уменьшению времени жизни атома в возбужденном состоянии. Форма спектральной линии, уширенной за счет столкновений, будет описываться функцией Лоренца, как и при естественном уширении. Но вместо Δω=γ=А_mn в (2) должно стоять Δω = 1/τ_р, где τ_р — время релаксации, определяемое процессами столкновений, так называемыми газокинетическими соударениями.

Оценим величину τ_р, например, для атомов неона при давлении Ра 60 Па а 0,5 мм рт. ст. (характерное давление в He-Ne лазере). Время релаксации будет приблизительно равно интервалу времени τ_ст между двумя столкновениями атомов Ne. Величину τ_ст в свою очередь можно оценить как отношение средней длины свободного пробега атома λ к средней тепловой скорости v_T. Из кинетической теории газов имеем

, (9)

где а_в — эффективный боровский радиус атома (молекулы); Р - давление газа. При комнатной температуре τ_ст ≈59*10^-7 с, чему соответствует ширина линии Δν ≈0,3 МГц.

Отметим, что τ_ст обратно пропорциональна, а ω₀ прямо пропорциональна давлению газа. Поэтому если уширение линии за счет столкновений в рассмотренном случае меньше доплеровского уширения, то для СО₂-лазеров, в которых рабочий газ находится при атмосферном давлении, столкновительное уширение может преобладать над доплеровским.

Особенно эффективно процессы релаксации из возбужденных состояний могут осуществляться в твердых телах при взаимодействии с колебаниями решетки. При этом τ_ст может составлять 10^-9 - 10^-12 с, приводя к существенным уширениям соответствующих спектральных линий.

Уширение за счет влияния внутренних (внутрикристаллических) и внешних электрического и магнитного полей. Этот механизм уширения определяется эффектами Зеемана и Штарка. Если зеемановское или штарковское расщепления меньше ширины каждого подуровня, то рядом расположенные подуровни частично перекрываются, вызывая уширение соответствующих спектральных линий.

В качестве активных материалов твердотельных лазеров широко используют различные кристаллы, в решетку которых введены специальные ионы - активаторы. К. ним, например, относится рубин - кристалл окиси алюминия А12О3, легированный хромом. Ионы хрома Сг³⁺ . являющиеся рабочими ионами, замещают ионы алюминия А1³⁺ и находятся под воздействием сильного внутрикристаллического электрического поля Е_кр, со стороны ближайших к ним ионов алюминия и кислорода, которое сдвигает и расщепляет энергетические уровни Сг³⁺. Тепловые колебания решетки приводят к тому, что внутрикристаллическое поле флуктуирует вокруг некоторого среднего значения. Это вызывает хаотическое смещение энергетических уровней Сг³⁺ и соответственно «флуктуации» спектральной линии, что эквивалентно ее уширению. Понижение температуры уменьшает флуктуации и ширину спектральной линии. Кроме того, вследствие возможного неоднородного окружения активного иона, обусловленного неоднородностями кристалла или посторонними дефектами, возникает дополнительное уширение суммарной линии. Последнее наиболее сильно проявляется в активированных стеклах, где окружение каждого из активных ионов различно. Могут быть и другие механизмы уширения спектральных линий, например вызванные неоднородностями среды.

Различают однородное и неоднородное уширение. Уширение называется однородным, если линии каждого отдельного атома и системы в целом уширяются одинаково. К однородному уширению относятся естественное уширение, уширение за счет процессов столкновений, и т. д. Уширение называется неоднородным, если резонансные частоты отдельных атомов не совпадают и распределяются в некоторой полосе частот, приводя к уширению линии системы в целом при существенно меньшем уширении линии отдельных атомов. К неоднородному уширению относятся доплеровское уширение, уширение за счет неоднородностей среды и т. д.

Форма однородно уширенных спектральных линий обычно хорошо описывается функцией Лоренца g_L(ω), а форма неоднородно уширенных линий - функцией Гаусса g_G(ω).

Подчеркнем, что в чистом виде спектральная линия будет уширена однородно или неоднородно в случае, когда преобладает какой-то один механизм уширения. Нередко общее уширение спектральной линии определяется одновременно несколькими механизмами. В этом общем случае форма линии будет определяться сверткой функций g₁(ω) и g₂(ω).

Приложение 1.

Источник: Гауэр Дж. – Оптические системы связи.

12.2Распределение нелетучей примеси в кристаллах, полученных зонной перекристаллизацией

5.3.1. Распределение нелетучей примеси в кристалле,

полученном после первого прохода расплавленной зоны

вдоль однородно легированного исходного слитка

Найдем распределение нелетучей примеси в кристалле, полученном после первого прохода расплавленной зоны вдоль однородно легированного исходного слитка. Пусть длина зоны равна l, поперечное сечение получаемого слитка, расплавленной зоны и слитка, играющего роль подпитывающей фазы, равны S. До этапа схода зоны со слитка объём расплавленной зоны остаётся неизменным в ходе процесса V^Ж = S·l = const. Поскольку примесь нелетуча, не будет происходить изменения её концентрации в паровой фазе dN^П = 0. Равновесный коэффициент распределения примеси будем считать постоянным (K₀ = const). Рассмотрим квазистатический режим кристаллизации, при котором примесь успевает однородно распределиться по всему объему расплавленной зоны (рис. 5.6). В этом случае уравнения материального баланса (5.4) и баланса объемов (5.5) примут вид

N^твdV^тв + V^жdN^ж + N^подпdV^подп = 0 , (5.11)

dV^тв + dV^подп = 0 . (5.12)

Рис.5.6. Схема процесса квазистатической зонной перекристаллизации

Проинтегрируем уравнение материального баланса примесного компонента (5.11) с учетом уравнения баланса объемов (5.12). Заменив в (5.12) dV^подп на - dV^тв , получим

dV^тв (N^тв – N^подп) = -V^ЖdN^ж. (1)

В соответствии с определением (5.1) для равновесного коэффициента распределением примеси и условием K₀ = const имеем

dN^ж = dN^тв/K₀ . (2)

Изменение объема твердой фазы представим в виде (см. рис. 5.6)

dV^тв= Sdx . (3)

Объем жидкой фазы до этапа кристаллизации последних порций расплава при сходе зоны со слитка будет равен

V^ж = Sl . (4)

С учетом (2) – (4) уравнение (1) примет вид

. (5)

После интегрирования обеих частей уравнения (5) в пределах, соответствующих изменению координаты x от нулевого до текущего значения, будем иметь

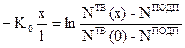, (6)

откуда находим

. (7)

Установим связь между N^тв (0) и N^подп. Поскольку N^подп = const (рассматриваем первый проход зоны вдоль однородно легированного исходного слитка), то после расплавления «первой» зоны, концентрация в ней легирующей примеси будет совпадать с N^подп . Первая бесконечно малая порция твердой перекристаллизованной фазы будет содержать примесные атомы с концентрацией

N^тв (0) = K₀ = K₀N^подп . (8)

Это позволяет переписать равенство (7) в виде

. (5.13)

Формула (5.13) дает теоретическое распределение примеси по длине перекристаллизованного слитка после первого прохода зоны в условиях:

• полного выравнивания состава жидкой фазы;
• отсутствия массового взаимодействия между паровой и конденсированными фазами;
• N^ПОДП = const;
• K₀ = const.

Она не описывает распределение примеси в хвостовой части перекристаллизованного слитка длинной l, где зона «сходит» со слитка и реализуется режим нормальной направленной кристаллизации. Там при K₀ < 1 в твердую фазу выделяется вся примесь, накопившаяся в расплавленной зоне. Формула (5.13) и рис. 5.7 показывают, что концентрация примеси заметно меняется лишь в начальной части кристалла.

N^ТВ/N^ПОДП

Рис. 5.7. Теоретические кривые распределения нелетучей примеси по длине кристалла, полученного однократной зонной перекристаллизацией однородно легированного исходного слитка. Числа у кривых указывают значения равновесного коэффициента распределения примеси

Однако зонная перекристаллизация может быть повторена многократно и тем самым может быть повышена степень очистки.

5.3.2. Многократная зонная перекристаллизация

Рассмотрим перераспределение примеси между твердыми фазами и расплавленной зоной длиной l при смещении фронта кристаллизации на величину dx вдоль слитка сечением S в очередном процессе многократной зонной перекристаллизации (рис. 5.8). Пусть N₀^ТВ(x) – распределение концентрации примеси в перекристаллизуемом слитке. Для рассматриваемого прохода зоны он играет роль подпитывающей фазы; N^ТВ(x) – распределение примеси в слитке после очередного прохода зоны.

При перемещении расплавленной зоны на dx (см. рис.5.8):

1) из жидкой фазы в кристаллизующийся объем Sdx перейдет N^ТВ(x)Sdx атомов примеси;

2) в расплавленную зону из перекристаллизуемого слитка поступит N₀^ТВ(x+l) Sdx атомов примеси и равномерно распределится по всему объёму зоны;

3) изменение количества атомов примеси в расплавленной зоне будет равно Q^Ж = N^Ж(x+dx) Sl – N^Ж(x) Sl.

Рис. 5.8. К выводу дифференциального уравнения для распределения концентрации нелетучей примеси вдоль слитка, полученного многократной зонной перекристаллизацией

Согласно условию материального баланса, разность между количеством атомов, поступивших в расплавленную зону из подпитывающей фазы при смещении фронта плавления, и вышедших из неё в растущий кристалл при смещении фронта плавления, будет равно изменению количества атомов в расплавленной зоне

N₀^тв(x+l)Sdx – N ^тв (x)Sdx = [N^ж(x+dx) – N^ж (x)]Sl . (5.14)

Используя в правой части (5.14) определение равновесного коэффициента распределения K₀ = (N ^тв/N^ж)_{ФР КР}, после сокращения на общий множитель S получим

[ (x+l) – N^ТВ(x)]dx = [N^ТВ(x+dx) – N^ТВ(x)], (1)

или, учитывая определение производной,

[ (x+l) – N^ТВ(x)] = . (2)

В итоге приходим к дифференциальному уравнению относительно концентрации нелетучей примеси в кристалле, получаемом при очередном квазистатическом проходе расплавленной зоны. Для сокращения записи равновесный коэффициент К₀ обозначим здесь через К

. (5.15)

Обсудим граничное условие для N^ТВ(x) при х = 0. Когда жидкая зона образуется в начале перекристаллизуемого слитка, концентрация примеси в расплаве будет равна

. (5.16)

Согласно определению (5.1) для равновесного коэффициента распределения, первые порции образующейся твердой фазы будут иметь концентрацию примеси

N^ТВ(0) = KN = . (5.17)

Для n-го прохода зоны вдоль одного и того же слитка уравнения (5.15) и (5.17) примут вид

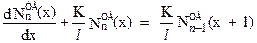, (5.18)

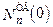= . (5.19)

Предельное теоретическое распределение примеси

в готовом слитке

После многократного прохода расплавленной зоны вдоль слитка в одном и том же направлении достигается предельное распределение примеси, которое не изменяется при последующих проходах зоны. Обозначим его N_∞^ТВ(x). В соответствии с (5.18) предельное теоретическое распределение будет удовлетворять уравнению

, (5.20)

решение которого имеет вид

= Ae^Bx , (5.21)

где А и В – некоторые постоянные величины, подлежащие определению. Подставляя (5.21) в (5.20) получаем трансцендентное уравнение для определения постоянной B

ABe^Bx + Ae^Bx = Ae^Bxe^Bl . (5.22)

После сокращения на общий, не равный нулю множитель Ae^Bx и некоторых преобразований, уравнение (5.22) упрощается и принимает вид

Bl = K(e^Bl – 1) . (5.23)

Уравнение для определения постоянной А найдем из условия сохранения полного количества атомов нелетучей примеси в слитке в ходе многократной зонной перекристаллизации

Q 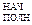= Q . (5.24)

При этом будем для простоты полагать, что распределение (5.21) реализуется до конца готового слитка длинной L. Т.е. предлагается экспоненциальная аппроксимация для распределения концентрации примеси в области «схода» зоны с готового кристалла. Предполагая далее, что исходный слиток легирован однородно с концентрацией примеси N₀, согласно (5.24) получаем

N₀SL = S . (5.25)

Согласно (5.25) с учётом (5.21) будем иметь

N₀L = A e^BL – 1), (5.26)

откуда для определения постоянной А получаем формулу

A = 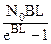. (5.27)

Как показывают численные оценки, теоретическое значение минимально достигаемой относительной концентрации примеси после многократной зонной перекристаллизации (N_∞^ТВ/N₀)_{MIN ТЕОР} составляет величину порядка 10^-32%. Реально получаемая в процессе многократной зонной перекристаллизации минимальная относительная концентрация примеси (N_∞^ТВ/N₀)_{MIN РЕАЛ} может достигать величины порядка 10^-12%.

В рассмотренных выше моделях зонной перекристаллизации не учтены многие факторы, свойственные реальным процессам. Важнейшими из них являются:

• взаимодействие расплава с паровой фазой;
• взаимодействие расплава с материалом контейнера;
• конечная скорость кристаллизации и наличие эффективного коэффициента распределения примеси (см. 5.4).

Билет 13