Спонтанное и вынужденное излучение. Коэффициенты Эйнштейна.

Рассмотрим процессы испускания и поглощения фотонов. Рассмотрение этих процессов будем проводить в рамках теории квантовых переходов. Эта теория основывается на законах сохранения энергии и импульса

,(1)

, (2)

где – угловая частота волны, - волновой вектор, и - энергия и импульс системы до взаимодействия с квантом света, и - после взаимодействия, и 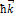- энергия и импульс фотона до взаимодействия, и - после взаимодействия.

Квантовый переход возможен, если в электромагнитном излучении присутствуют компоненты с частотами, удовлетворяющими правилу частот Бора.

(3)

Возьмем для рассмотрения два энергетических состояния Е_m и E_n. Пусть Е_m > E_n, тогда из закона сохранения энергии следует три возможных процесса взаимодействия фотона с атомом.

Рис. 1. а — спонтанный переход с испусканием фотона; б — вынужденный переход с поглощением фотона; в — вынужденный (индуцированный) переход с испусканием фотона

1)Если

В результате взаимодействия система перешла из более высокого энергетического состояния в более низкое с испусканием кванта света. Такой процесс называется спонтанным испусканием фотона.

2)Если

Система перешла из более низкого энергетического состояния в более высокое с поглощением кванта света. Данный процесс называется резонансным поглощением фотона.

3)Если

В результате системам перешла из более высокого энергетического состояния в более низкое с испусканием кванта света. В качестве вынуждающего фактора, определяющего подобный переход выступает фотон той же частоты что и испускаемый. Такой процесс называется вынужденным (индуцированным) испусканием фотона.

Коэффициенты Эйнштейна.

1. Вероятность спонтанного перехода с уровня Е_m на E_n за время dt с испускание кванта света можно выразить соотношением

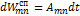,(4)

где— 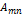коэффициент Эйнштейна для спонтанных переходов. Его значение не зависит от внешних воздействий и определяется только свойствами данной квантовой системы.

Величина, обратная называется спонтанным временем жизни для переходов m→n

.

Значение коэффициента Эйнштейна А_mn для разрешенных переходов в оптическом диапазоне составляет10⁸ с^-1, а для запрещенных 1 с^-1.

Спонтанное излучение ненаправленно, некогерентно, неполяризованно и немонохроматично. Такое естественное излучение в оптическом диапазоне испускают все известные «классические» источники света (лампы накаливания, газоразрядные лампы, люминесцентные лампы и т. д.).

2. Вероятность поглощения фотона с частотой

,обусловленная переходом n→m за интервал времени dt:

, (5)

где В_nm — коэффициент Эйнштейна для вынужденных (индуцированных) переходов с поглощением; ρ(ω)—спектральная плотность излучения.

3. Вероятность индуцированного испускания фотона за интервал времени dt:

, (6)

где В_mn — коэффициент Эйнштейна для вынужденных (индуцированных) переходов с испусканием.

Вынужденное излучение является когерентным. Такое излучение в оптическом диапазоне испускают только оптические квантовые генераторы — лазеры.

Определим связь между коэффициентами , , .

Рассмотрим совокупность атомов (молекул), находящихся в термодинамическом равновесии со стенками окружающего объема при температуре Т. Пусть на уровне Е_m находится N_m частиц, а на уровне E_n - N_n частиц. Тогда число поглощенных квантов света за интервал времени dt

; (7)

число квантов света, испущенных в результате спонтанных переходов:

; (8)

число квантов света, испущенных в результате индуцированного испускания:

. (9)

Условие термодинамического равновесия означает, что суммарное число квантов света, испущенных системой, равно числу поглощенных квантов света:

(10а)

или

(10б)

В условиях равновесия распределение атомов (молекул) по энергетическим уровням подчиняется распределению Больцмана:

(11)

где N — полное число частиц в системе;

q_m и q_n — статический вес уровней Е_m и E_n (или степень вырождения).

Для невырожденных уровней q_m = q_n = 1. Знаком Σ обозначена статистическая сумма

где суммирование проводится по всем энергетическим состояниям i.

Из (11) следует, что

Величина, равная отношению числа частиц в единице объема на данном энергетическом уровне к его статистическому весу, называется населенностью энергетического уровня Подставляя (11) в (10б), получаем

(12)

или

(13)

Эти соотношения справедливы при любых температурах, в том числе при T→∞. При условии , т. е. при малых частотах и больших температурах, спектральная плотность излучения определяется классической формулой Рэлея — Джинса:

При T→∞, ρ→∞, , и из (13) получаем первое соотношение между коэффициентами Эйнштейна для вынужденных переходов:

(14)

В случае, если кратности вырождения уровней Е_m и E_n равны,

.

Найдем соотношение между коэффициентами А_mn и В_mn. Для этого из (13) получим, предполагая, что

(15)

При больших температурах, когда Е_m – Е_n << kТ, можно разложить экспоненту в ряд и ограничиться первым после единицы членом разложения, откуда имеем

(16)

В условиях термодинамического равновесия при kT >> ћω спектральное распределение ρ(ω) должно определяться формулой Рэлея — Джинса. Сравнивая ее с формулой (16), видим:

(17)

(18)

Таким образом, условие частот Бора (17) вытекает из проведенного рассмотрения. Второе соотношение между коэффициентами Эйнштейна (18) позволяет связать коэффициент спонтанного испускания с показателем поглощения, который может быть найден непосредственно из измерений.

Для характеристики вероятности перехода часто используют понятие времени жизни атома в возбужденном состоянии.

Пусть в момент времени t=0 имеется атомов в возбужденном состоянии Е_m и опустошение этого состояния возможно только за счет спонтанных переходов m→n. Тогда уменьшение населенности верхнего уровня за время dt выразится формулой

(19)

где A_mn – есть вероятность того, что один атом покинет это состояние за единицу времени.

Так, как A_mn есть постоянная величина, то решение уравнения имеет вид

(20)

где .

Определим среднее время пребывания атома в возбужденном состоянии. По определению среднего,

(21)

(т.к )

Таким образом, величина выражает среднее время пребывания (время жизни) атома в возбужденном состоянии, ограниченное спонтанными переходами m→n.Она равна среднему времени пребывания атома в возбужденном состоянии.

Из (19) и (20) получаем закон затухания мощности спонтанного излучения

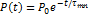(22)

где .

Кроме оптических излучательных переходов, обусловленных взаимодействием с электромагнитным излучением, возможны неоптические квантовые переходы из одного состояния в другое, которые называются безызлучательными. Такие переходы, в частности, могут происходить при столкновениях атомов и молекул газа как друг с другом, так и с электронами или со стенками сосуда. Особенно эффективны безызлучательные процессы в твердом теле при взаимодействии с колебаниями кристаллической решетки.

11.2 Распределение нелетучей примеси в кристаллах, полученных методом нормальной направленной кристаллизации и методом Чохральсого

При получении методом нормальной направленной кристаллизации и методом Чохральсого монокристаллов, легированных слаболетучей примесью (например, бором), с достаточной точностью выполняются условия: dV^подп = 0 – так как нет подпитки из твердой фазы; V^пdN^п = 0 – можно пренебречь массовым взаимодействием расплава с паровой фазой, так как примесь нелетучая. Вследствие этого для рассматриваемых методов уравнения баланса (5.4) и (5.5) принимают вид

N^твdV^тв + d(N^жV^ж) = 0 , (5.6)

dV^тв + dV^ж = 0 . (5.7)

Характер распределения примеси в растущем кристалле и расплаве для К₀= <1 и двух последовательных моментов времени показан схематически на рис. 5.4. Режим кристаллизации предполагается квазистатическим.

Распределение примеси вдоль кристаллизуемого слитка найдем путем интегрирования уравнения баланса массы (5.6), которое с учетом уравнения баланса объемов (5.7) можно записать в виде

. (5.8)

Рис. 5.4. Характер распределения примеси в растущем кристалле и расплаве для K₀= <1 и двух последовательных моментов времени

Разделим переменные в этом уравнении и перейдем к переменным V^ж и N^тв

, (1)

. (2)

Преобразуем правую часть уравнения (2), используя определение К₀= и учитывая, что К₀ = const. Используя равенство , добьемся того, чтобы в правой части фигурировало только N^тв

. (3)

Проинтегрируем (3) в пределах, соответствующих начальному и текущему состоянию процесса нормальной направленной кристаллизации

, (4)

. (5)

Рассмотрим левую часть уравнения (5). По условию баланса объемов

, (6)

где введено обозначение g для доли закристаллизовавшегося расплава

. (5.9)

С учетом (5.9) формулу (5) можно представить в виде

, (7)

откуда получаем

. (8)

Величина при квазистатической кристаллизации зависит от начального уровня легирования расплава и равновесного коэффициента распределения примеси

. (9)

С учетом (9) формула (8) может быть записана в виде

. (5.10)

Формула (5.10) дает теоретическое распределение примеси по длине кристалла при его выращивании по методу Чохральского или методу нормальной направленной кристаллизации в условиях:

· полного выравнивания составов в жидкой фазе;

· отсутствия подпитки;

· отсутствия массового взаимодействия расплава с паровой фазой (примесь нелетучая);

· =const.

Результаты некоторых расчётов по формуле (5.10) представлены на рис. 5.8.

Рис. 5.8. Теоретические кривые распределения нелетучей примеси по длине кристалла полученного методом Чохральского или методом нормальной направленной кристаллизации при ; цифры на кривых–значения равновесного коэффициента распределения

В рассмотренной модели не учтён целый ряд явлений, свойственных реальным процессам получения монокристаллов методом нормальной направленной кристаллизации и методом Чохральского:

· взаимодействие расплава с паровой фазой;

· взаимодействие расплава с материалом контейнера;

· конечная скорость кристаллизации и наличие эффективного коэффициента распределения (см. 5.4).

Билет №11

3.Диэлектрическая нелинейность сегнетоэлектриков в постоянном электрическом поле.Области применения.Механизмы равновесной нелинейности.