Свойства плоского резонатора

Рассмотрим резонатор, образованный двумя плоскими квадратными зеркалами с размерами 2а x 2а, находящимися на расстоянии L друг от друга, как показано на рис. 2.13. Собственные частоты в первом приближении определяются выражением (2.24). Их можно найти, положив L₁=L₂=2a и L₃=L. Поскольку (m, n)«q, разлагая (2.24) в степе нной ряд, имеем

Рисунок 2.13 К определению свойств плоского резонатора

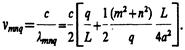(Пихтин) (2.30)

Разность частот между двумя неаксиальными колебаниями, отличающимися друг от друга на единицу по индексу m, получается из (2.30) с учетом (2.26) :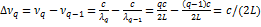

(Пихтин) (2.32)

Аналогично находят расстояние по частоте для двух типов колебаний (мод), отличающихся друг от друга на единицу по индексу n:

(Пихтин) (2.32a)

Неаксиальные моды, отличающиеся значениями n или m, будут различаться распределением поля в плоскости, ортогональной оси z, т. е. в поперечном направлении. Поэтому неаксиальные моды называют также поперечными модами. Для поперечных мод с различными индексами m структура поля будет различной в направлении х, а с n — в направлении у.

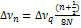
где N=a²/(λL) ­ безразмерный параметр, называемый числом Френеля.

Оценим соответствующие величины для типичного случая λ=1 мкм, L=l м и 2а =1 см. Число Френеля N=25»1, и расстояние между неаксиальными колебаниями ( , ) порядка мегагерц, т. е. существенно меньше расстояния между аксиальными колебаниями ( 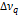≈ 150 МГц) [см. (2.26)]. Дифракционные потери для неаксиальных мод выше, чем для аксиальных, поэтому добротность первых меньше.

Спектр собственных частот плоского резонатора как для аксиальных, так и для некоторых неаксиальных колебаний показан на рис. 2.14. Расстояние по частоте между аксиальными модами 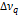увеличивается при уменьшении длины резонатора L, а между неаксиальными модами ( и ) — при уменьшении числа Френеля N. Из (2.30) видно, что моды с одинаковыми q, но разными тип, удовлетворяющими условию m² +n² = const, имеют одну и ту же частоту. Такие моды называют частотно вырожденными.

Как нетрудно заметить, для резонатора с зеркалами прямоугольной формы индексы m и n характеризуют число изменений направления поля вдоль осей х и у соответственно. На рис. 2.16 показана структура электрического поля для простейших типов колебаний, а на рис. 2.17 — фотографии структуры светового поля на зеркалах резонатора гелий-неонового лазера. С увеличением индексов тип амплитуда поля на краях зеркала возрастает. Она минимальная для аксиальных ТЕМ₀₀-колебаний.

Рисунок 2.16 Структура поля для некоторых типов колебаний в плоском резонаторе с квадратными зеркалами

Распределение поля внутри резонатора с плоскими зеркалами в разных сечениях, перпендикулярных оптической оси, изменяется незначительно. Это позволяет достаточно эффективно использовать активный объем рабочего вещества.

Недостатком плоского резонатора, с точки зрения его практического применения, является трудность юстировки: параллельность зеркал друг относительно друга должна быть выдержана с точностью несколько угловых секунд. Этого недостатка лишены резонаторы со сферическими зеркалами.

оптические резонаторы со сферическими зеркалами. Конфокальный резонатор. Устойчивые и неустойчивые резонаторы. Селекция поперечных и продольных мод оптического резонатора.

Резонаторы со сферическими зеркалами.

Широкое распространение в лазерной технике получили оптические резонаторы, образованные двумя сферическими или одним сферическим и одним плоским зеркалами. Различные типы резонаторов со сферическими зеркалами представлены на рис. 2.19, а — г. Особое место среди них занимает конфокальный резонатор, на свойствах которого остановимся подробнее.

Рисунок 2.19 Типы резонаторов со сферическими зеркалами: а) — конфокальный (R₁=R₂=L); б) — полуконфокальный (R1=2L R₂=∞); в) — концентрический (R₁= R₂=L/2); г) — полуконцентрический (R₁=L R2=∞); д)—неустойчивый резонатор, общий случай; е) — телескопический неустойчивый резонатор

1. Конфокальный резонатор (рис. 2.19, а). Конфокальным называют открытый резонатор, образованный одинаковыми сферическими зеркалами, оси и фокусы которых совпадают. Так как фокус сферического зеркала радиусом R расположен на расстоянии R/2, то это означает, что радиусы кривизны зеркал равны длине резонатора.

Для сферических зеркал квадратного сечения со стороной 2а при условии a«L и N> 1 собственные функци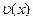и (или ) апроксимируются произведением полиномов Эрмита 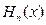на гауссову функцию . В системе координат, начало которой совпадает с фокальной точкой F резонатора, а ось z -— с осью резонатора, поперечное распределение поля дается выражением

(2.39)

где Н_m и Н_n — полиномы Эрмита.Для первых 4-ёх степеней они имеют вид

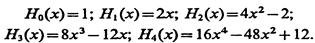
Выражение (2.39) описывает поперечные распределения поля для ТЕМ_mnq-мод в конфокальном резонаторе. На рис. 2.20 показаны эти распределения для первых трех мод. Радиус r_1/e в (2.39) характеризует поперечный размер пучка.

Для основной ТЕМ₀₀-моды наблюдается гауссово распределение интенсивности:

(2.39a)

Значение r_1/e определяет размер поперечного сечения, где интенсивность поля падает в е раз. В пятне площадью πr_1/e² сосредоточена основная энергия волны, проходящей в направлении z через плоскость ху. Ширина пятна меняется вдоль оси z по закону

(2.40)

Рисунок 2.20 Распределение поля в конфокальном резонаторе для первых трех мод: а) аналогично рис. 2.15, но по оси абсцисс отложена величина х/r_1/e где радиус пятна r_1/e определяется соотношением (2.40);

Эта зависимость представлена на рис. 2.21 сплошное линией. В фокальной плоскости при z = 0 радиус пучка минимален. Он называется радиусом перетяжки или радиусом шейки каустики и равен

(2.41)

На поверхности зеркала при z=L/2 радиус пучка раз больше, чем в центре.

Пучок, распределение поля в поперечном сечении которого характеризуется функцией Гаусса, называется гауссовым пучком. Поверхности равных фаз для гауссова пучка представляют собой сферические поверхности. Радиус кривизны синфазной поверхности, пересекающей оптическую ось резонатора в точке z (напомним, что начало отсчета совпадает с общим фокусом зеркал), определяется соотношением

(2.42)

След этих поверхностей изображен на рис. 2.21 пунктирными линиями. С приближением к центру резонатора радиусы кривизны синфазных поверхностей увеличиваются. При z = 0 , т. е. синфазная поверхность является плоской. При z= ±L/2 радиус R=±L, т. е. поверхности зеркал в конфокальном резонаторе являются поверхностями равных фаз. При больших z»L/2, что соответствует дальней зоне, волновой фронт (2.42) приближается к волновому фронту сферической волны (R≈z), распростра-няющейся из точки, расположенной на оси пучка в месте пере- тяжки.

Таким образом, ТЕМ_оо-мода конфокального резонатора представляет собой сферическую волну, распространяющуюся из его центра и обладающую гауссовым распределением интенсивности в плоскости, перпендикулярной направлению распространения. Основная часть энергии пучка, как следует из (2.39а), сосредоточена в телесном угле

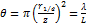(2.43)

Рисунок 2.21 Размер освещенного пятна r_1/e, синфазные поверхности и распределение интенсивности для аксиальной ТЕМ₀₀-моды в конфокальном резонаторе

Обратим внимание, что расходимость пучка в основной моде конфокального резонатора определяется не поперечным, а продольным размером L резонатора. Аналогично, поперечный размер пучка r_1/е, определяемый (2.40), не зависит от поперечного размера зеркала 2α. Это является следствием сделанных выше предположений о малости значения отношения (α/L) и о большом значении числа Френеля .

Собственным функциям уравнения дающим попереч ные распределения, соответствуют собственные частоты, определяемые условием

(2.44)

Отсюда видно, что спектр собственных частот конфокального резонатора сильно вырожден: изменение m и n такое, что дает одно и то же значение частоты.

Перечисленные особенности распределения поля в конфокальном резонаторе имеют как преимущества, так и недостатки. Например, по сравнению с плоским резонатором поле в конфокальном резонаторе более плотно сконцентрировано у его оси и спадает на краях значительно быстрее. Это приводит к тому, что дифракционные потери в конфокальном резонаторе очень малы, в том числе для неаксиальных колебаний высокого порядка. Поэтому конфокальный резонатор не очень чувствителен к разъюстировке зеркал. Однако эта же причина затрудняет получение одномодового режима генерации и мешает полностью использовать объем активного вещества в резонаторе.

Ниже мы покажем, что конфокальный резонатор лежит на границе, разделяющей устойчивую и неустойчивую области. Поэтому в чистом виде конфокальный резонатор применяют редко. Если желательно сохранить симметрию резонатора, то применяется квазиконфокальный резонатор, расстояние между зеркалами которого отличается от L=R на небольшую величину α:

L/R = l ± α, α«1.

Небольшие значения а, не изменяя по существу характер распределения поля в резонаторе, делают его устойчивым.

2. Резонаторы с произвольными сферическими зеркалами. Эти резонаторы состоят из двух соосных сферических зеркал радиусами R₁ и R₂, расположенных на расстоянии L друг от друга. Свойства таких резонаторов легко определить, если найдена соответствующая конфокальная система, в которой две синфазные поверхности совпадают с поверхностями зеркал резонатора. Если известны радиусы R₁ и R₂ зеркал и расстояние между ними, то из выражения (2.42) можно найти длину, а также радиусы кривизны и координаты зеркал эквивалентного конфокального резонатора. Если известно , то распределение поля внутри и вне резонатора будет таким же, как в эквивалентном конфокальном резонаторе. В частности, радиус светового пятна будет определяться соотношением (2.40), где вместо L будет стоять . Если резонатор образован двумя одинаковыми сферическими зеркалами радиусами R₁=R₂=R, расположенными на расстоянии L друг от друга, то из (2.42) получаем, что длина эквивалентного конфокального резонатора

(2.45)

Эквивалентный конфокальный резонатор определяет только собственные функции произвольного сферического резонатора.

Нахождение собственных значений не может быть сведено к задаче о конфокальном резонаторе. В частности, собственные частоты в общем случае будут определяться не соотношением (2.44), а более сложными выражениями. В обобщенном сферическом резонаторе частотное вырождение мод обычно исчезает.

Сферический резонатор может быть либо устойчивым, либо неустойчивым (в последнем случае резонатор теряет свои резонансные свойства). Например, если резонатор образован двумя одинаковыми сферическими зеркалами радиусами R, причем L>2R, то, как следует из (2.45), ему невозможно подобрать эквивалентный конфокальный резонатор. Это означает, что в таких резонаторах невозможно образование устойчивого стационарного распределения электромагнитного поля с малыми потерями.

Пусть R₁ и R₂ — радиусы зеркал, a L — расстояние между ними. Можно показать, что резонатор будет устойчивым и ему всегда можно подобрать эквивалентный конфокальный резонатор, если выполняется неравенство

(2.46)

На рис. 2.22 приведена диаграмма, иллюстрирующая условие устойчивости оптических резонаторов. Устойчивые области соответствуют заштрихованным участкам.

Рисунок 2.22 Диаграмма устойчивости оптических резонаторов со сферическими зеркалами

Отметим характерные точки на этой диаграмме. Точке А с координатами (—1;—1) соответствует резонатор с плоскими зеркалами, расположенный на границе устойчивости. Точке В с координатами (0;0) соответствует конфокальный резонатор. Точке С с координатами (1;1) соответствует резонатор, образованный двумя одинаковыми сферическими зеркалами, оси и центры кривизны которых совпадают, т. е. R₁ =R₂=L/2. Такой концентрический резонатор в) также лежит на границе, разделяющей устойчивую и неустойчивую области. Дифракционные потери в нем очень быстро возрастают с увеличением типа колебаний, т. е. с увеличением индексов m и n. Поэтому такой резонатор наряду с неустойчивыми резонаторами применяют для селекции (отбора) неаксиальных колебаний.

Точкам D и D' с координатами (—1 —0,5) и (0,5;—1) соответствует полуконфокальный резонатор, т. е. резонатор, образованный одним плоским и одним сферическим зеркалом, радиус кривизны которого равен удвоенной длине резонатора. б). Он находится в середине устойчивой области, и его свойства аналогичны конфокальному резонатору с удвоенной длиной. Такой резонатор часто применяют на практике. Точкам Е и Е’ с координатами (—1;0) и (0;—1) соответствует полуконцентрический резонатор, он обладает особенностями, характерными для концентрического резонатора.

Неустойчивые резонаторы и селекция поперечных типов колебаний.

В ряде случаев требуется обеспечить такой режим работы лазера, при котором генерация осуществлялась бы на одной, как правило, продольной моде. Такой режим называется одномодовым. Для его осуществления необходимо выделить (селектировать) основную моду при подавлении поперечных мод. Это можно сделать за счет увеличения потерь при увеличении поперечных индексов мод m и n. Но в устойчивых резонаторах дифракционные потери существенно меньше потерь на частичное пропускание зеркал, а потому добротность Q резонатора для аксиальных (продольных) и неаксиальных (поперечных) колебаний низших порядков слабо зависит от m и n. В этом случае разница в дифракционных потерях не может служить основой для селекции колебаний, но она может быть основана на различии в пространственном распределении поля мод с различными поперечными индексами m и n. Поскольку в резонаторах со сферическими зеркалами основная ТЕМ_оо-мода имеет гауссово распределение с минимальной шириной пучка r_1/e, то простейшим и часто применяемым на практике способом селекции является диафрагмирование пучка внутри резонатора. Для этого внутри резонатора помещают диафрагму, размер отверстия которой примерно равен поперечному размеру моды, следующей за основной, т. е. TEM₁₀-моды (см, рис. 2.20). Такая диафрагма будет создавать большие потери для неаксиальных колебаний, большая часть энергии которых сосредоточена по периферии. Очевидно, что при наличии диафрагмы внутри резонатора число Френеля N будет определяться не поперечным размерим зеркала, а размером отверстия этой диафрагмы.

Недостатками обсуждавшегося выше способа выделения основной ТЕМ₀₀-моды в устойчивом резонаторе являются: а) малость поперечных размеров моды и, как следствие, малость используемого объема активного вещества; б) внесение дополнительных потерь в основную моду.

В мощных лазерах, где необходимо применение большого объема активного вещества, эффективным средством селекции поперечных мод является переход к неустойчивым резонаторам. В неустойчивых резонаторах, параметры которых попадают в не заштрихованные области диаграммы (см. рис. 2.22), дифракционные потери даже основной моды велики и превосходят все остальные виды потерь. Для поперечных мод потери очень быстро нарастают при увеличении индексов m и n. Именно это обстоятельство приводит к эффективному выделению основной моды. В качестве примера на рис. 2.19, д и 2.19, е показаны два типа неустойчивых резонаторов.

Неустойчивые резонаторы могут быть применены лишь в лазерах с большим показателем усиления. Это обусловлено необходимостью компенсации больших потерь излучения за один проход, принципиально присутствующих в таких резонаторах. Важно, что это излучение, стремящееся выйти из резонатора (рис. 2.19, д—е), может быть использовано как полезное выходное излучение лазера. К достоинствам неустойчивых резонаторов относятся: а) возможность использования больших объемов активного вещества, что связано с отсутствием фокусировки излучения (гауссова сжатия) к оси резонатора; б) возможность эффективной селекции поперечных типов колебаний; в) возможность использования только отражающей оптики (например, металлических зеркал) как для создания резонатора, так и для вывода излучения, а также простота управления выводимой из резонатора энергии и достижения оптимальных условий вывода излучения.

Недостатком неустойчивых резонаторов, ограничивающим их применение мощными лазерами, является необходимость применения активных сред с большим показателем усиления. Кроме того, поперечное сечение выходного пучка света в ближней зоне, как видно из рис. 2.19, е, имеет форму кольца (для круглых зеркал), что не всегда удобно. Однако вдали от выходного зеркала, в дальней зоне, темное пятно в центре исчезает.

Составные и дисперсионные резонаторы. Селекция продольных типов колебаний.

Рассмотренные выше резонаторы не могут селектировать продольные типы колебаний, т. е. ТЕМ_00q-моды, различающиеся по индексу q, поскольку дифракционные потери для них одинаковы. Для осуществления селекции продольных мод может быть использовано их отличие друг от друга по частоте [см. (2.26), (2.30)], для чего необходимо внутрь резонатора ввести узкополосный дисперсионный (т. е. частотно зависимый) элемент. В качестве такого элемента могут быть использованы призмы, дифракционные решетки, специальные зеркала с частотно зависимым коэффициентом отражения, а также дополнительные резонаторы типа плоского резонатора (эталона Фабри — Перо) с малой базой.

Два или более связанных между собой резонатора (1 — 3 и 1 — 2) образуют составной резонатор. Его схема приведена на рис. 2.23, а. Зеркало 3 — полупрозрачное. Свойства такого резонатора аналогичны свойствам двух связанных контуров. Как видно из рис. 2.23, б, при соответствующем выборе величин L₂, L₁ и коэффициента пропускания зеркала 3 составной резонатор способен селектировать аксиальные колебания (сравните с рис. 2.11).

Рисунок 2.23 Схема составного резонатора (а) и зависимость добротности его аксиальных типов колебаний от частоты (б)

Рисунок 2.24 Дисперсионные резонаторы: а) призменный; б) составной решеточный: 1 — дифракционная решетка, 2 — эталон Фабри—Перо (плоский интерферометр), 3 — телескопическая система, 4 — зеркало резонатора

Меняя угол разворота призмы, можно осуществлять перестройку частоты.

Дисперсиипризмы часто бывает недостаточно для получения одночастотной генерации с высокой степенью монохроматичности и для тонкой перестройки частоты лазерного излучения. Для этой цели применяют более сложные дисперсионные резонаторы (рис. 2.24, б). Дифракционная решетка 1 выполняет роль грубого дисперсионного элемента. Эталон Фабри — Перо 2 позволяет выделить одну продольную моду. Телескопическая система 3, состоящая из одной или нескольких линз, служит для расширения пучка, выходящего из активного элемента, и уменьшения его угла расходимости, что необходимо для эффективной работы как дифракционной решетки, так и эталона. Грубая перестройка частоты осуществляется поворотом дифракционной решетки, а точная – поворотом эталона Фабри -Перо.