
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пояснения к решению задач 3.1÷3.10
Задачи 3.1÷3.10решаются с помощью уравнения Бернулли:

Сложность решения таких задач заключается не только в том, что приходится определять потери напора на участке между выбранными сечениями, но и в правильном выборе самих сечений. Поэтому при использовании уравнения Бернулли целесообразен следующий порядок действий.
1. Выбор сечений. Сечения нужно выбирать в таких местах, где поток является плавно изменяющимся. Если искомой величиной является z, p или v в некотором сечении потока, то следует выбрать это сечение, а другое – в том месте, где величины z, p или v известны или их модно определить по условию задачи.
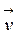 Если искомой величиной является расход, то сечения нужно выбирать там, где
Если искомой величиной является расход, то сечения нужно выбирать там, где
z и p известны. Сечения должны быть перпендикулярными к направлению движения жидкости (к вектору скорости ).
2. Выбор положения плоскости 0-0 отсчета z. Плоскость 0-0, от которой рассчитывается z, должна проводиться всегда горизонтально. Ее целесообразно проводить через центр того сечения, которое расположено ниже. Если центр какого-либо сечения окажется ниже плоскости 0-0, то z нужно брать со знаком минус.
3. Нумерация сечений. Нумеровать сечения нужно так, чтобы жидкость двигалась от сечения 1-1 к сечению 2-2. Для этого следует предварительно выяснить, в каком их выбранных сечений напор

больше и затем воспользоваться тем, что жидкость всегда движется от сечений с большим напором к сечению, где напор меньше.
4. Определение величин z, p и v в выбираемых сечениях. Целесообразно составить таблицу:
| Сечение 1-1 | Сечение 2-2 |
| z1= | z2= |
| p1= | p2= |
| v1= | v2= |
При заполнении таблицы, давления следует принимать либо оба абсолютными, либо оба избыточные. Скорости в сечениях, совпадающих со свободными поверхностями жидкости в баках, обычно принимают равным нулю.
 5. Составление уравнения Бернулли и решение его относительно искомой величины. Уравнение Бернулли записывается с учетом таблицы значений z, p и v. Перед началом числового расчета следует определить числовые значения всех входящих в уравнение величин применительно в выбранной системе единиц измерения (рекомендуется система СИ). Если в уравнении Бернулли остаются неизвестными скорости v1 и v2, то нужно дополнительно использовать уравнение неразрывности потока.
5. Составление уравнения Бернулли и решение его относительно искомой величины. Уравнение Бернулли записывается с учетом таблицы значений z, p и v. Перед началом числового расчета следует определить числовые значения всех входящих в уравнение величин применительно в выбранной системе единиц измерения (рекомендуется система СИ). Если в уравнении Бернулли остаются неизвестными скорости v1 и v2, то нужно дополнительно использовать уравнение неразрывности потока.
где Q1, Q2 – расходы;
w1, w2 – площади поперечных сечений потока.
В некоторых случаях приходится составлять уравнение Бернулли для двух пар сечений и из этих двух уравнений находить искомые величины.
При решении задач требуется определить суммарные потери напора на участке системы между выбранными сечениями (hw). При последовательном соединении гидравлических сопротивлений

где hl – потери напора по длине (характеризуют гидравлические сопротивления по длине);
hM – местные потери напора (характеризуют местные гидравлические сопротивления).
 Потери напора по длине определяются из выражения (формула Дарси)
Потери напора по длине определяются из выражения (формула Дарси)
где λ – коэффициент гидравлического трения. Величина λ зависит от режима движения жидкости и относительной шероховатости.
При ламинарном режиме (Re<2000) для вычисления λ следует пользоваться зависимостью λ=64/ Re, а α = 2.
При переходном режиме (2000<Re<5000) коэффициент гидравлического трения λ можно определить либо по графику Мурина, либо по формуле, рекомендуемой для расчета λ в рассматриваемом режиме, например:

(формула Альтшуля).
При турбулентном режиме (Re>5000) коэффициент α = 1, а λ определяется либо по графику Мурина, либо по рекомендуемой формуле (можно применять преобразованную формулу Альтшуля:

Потери напора местные (hM) определяются по выражению (формула Вейсбаха):
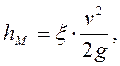
где ξ – коэффициент местных сопротивлений, зависящий от вида местного гидравлического сопротивления.
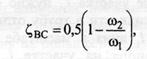 При вычислении потери напора на входе в трубу коэффициент местного сопротивления ζвx = 0,5. Значение коэффициента местного сопротивления при внезапном сужении трубопровода
При вычислении потери напора на входе в трубу коэффициент местного сопротивления ζвx = 0,5. Значение коэффициента местного сопротивления при внезапном сужении трубопровода
где ω1 — площадь широкого сечения трубы; ω2 — площадь узкого сечения трубы.
Потерю напора при внезапном расширении трубопровода можно определить по формуле Борда:
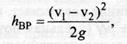
где v1 и v2 — средние скорости течения соответственно до и после расширения.
После определения потерь напора по длине и в местных сопротивлениях вычисляют искомую величину — напор Н в резервуаре.
Строят напорную линию (для рисунка 1). Напорная линия показывает, как

Рис. 1.
изменяется полный напор  (полная удельная энергия) по длине потока. Значения Н откладывают от осевой линии трубопровода.
(полная удельная энергия) по длине потока. Значения Н откладывают от осевой линии трубопровода.
При построении напорной линии нужно вертикалями выделить расчетные участки. Таких участков в данной задаче будет три. Далее в произвольно выбранном вертикальном масштабе откладывают от осевой линии величину найденного уровня жидкости в резервуаре H. Проводя по этому уровню горизонтальную линию, получаем линию исходного (первоначального) напора. От уровня жидкости в резервуаре по вертикали, отвечающей сечению при входе жидкости в трубопровод, откладывают в масштабе вниз отрезок, равный потери напора при входе жидкости в трубу (потеря напора в местном сопротивлении).
На участке 11 имеет место потеря напора по длине трубопровода hl1. Для получения точки, принадлежащей напорной линии в конце участка l1, нужно от линии полного напора после входа жидкости в трубу отложить по вертикали в конце участка l1 вниз в масштабе отрезок, соответствующий потере напора на участке l1 .Затем от точки полного напора в конце участка 11 откладывается в масштабе по вертикали отрезок, соответствующий потере напора в местном сопротивлении (внезапное расширение или сужение), и так до конца трубопровода. Соединяя точки полного напора, получим напорную линию.
Пьезометрическая линия показывает, как изменяется пьезометрический напор z + р/γ (удельная потенциальная энергия) по длине потока. Удельная потенциальная энергия меньше полной удельной энергии на величину удельной кинетической энергии av2/2g. Поэтому, чтобы построить пьезометрическую линию, нужно вычислить на каждом участке величину av2/2g и отложить ее числовое значение в масштабе вниз по вертикали от напорной линии. Откладывая соответствующие значения av2/2g в начале и в конце каждого участка и соединяя полученные точки, строим пьезометрическую линию.
График напорной и пьезометрической линий будет построен правильно в том случае, если при их построении были выдержаны принятые вертикальный и горизонтальный масштабы, а также верно вычислены все потери напора и все скоростные напоры av2/2g.
Для того чтобы проверить правильность построения напорной и пьезометрической линий, необходимо помнить следующее:
1. Напорная линия вниз по течению всегда убывает. Нигде и никогда напорная линия не может вниз по течению возрастать.
2. Поскольку потеря энергии потока на трение зависит от скорости движения жидкости, интенсивность потери напора (потеря напора на единицу длины или гидравлический уклон) будет больше на том участке, где скорость больше. Следовательно, на участках с меньшими диаметрами и большими скоростями наклон напорной и пьезометрической линий будет больше.
3. В отличие от напорной, пьезометрическая линия может вниз по течению как убывать, так и возрастать (при переходе с меньшего сечения на большее).
4. В пределах каждого участка пьезометрическая линия должна быть параллельна напорной, поскольку в пределах каждого участка постоянна величина av2/2g.
5. На тех участках, где скорость больше, расстояние между напорной и пьезометрической линией больше.
6. Как бы ни изменялась пьезометрическая линия по длине потока, при выходе его в атмосферу (свободное истечение) она неизбежно должна приходить в центр тяжести выходного сечения. Это происходит потому, что пьезометрическая линия показывает изменение избыточного давления по длине трубопровода, которое в выходном сечении равно нулю. После построения напорной и пьезометрической линий на графике показывают все потери напора и все скоростные напоры с указанием их численных значений, Примерный вид графика приведен на рис. 2.
 После построения напорной и пьезометрической линий на графике показывают все потери напора и все скоростные напоры с указанием их численных значений, Примерный вид графика приведен на рис. 2.
После построения напорной и пьезометрической линий на графике показывают все потери напора и все скоростные напоры с указанием их численных значений, Примерный вид графика приведен на рис. 2.
Рис.2.
Дата добавления: 2015-04-18; просмотров: 1111; Мы поможем в написании вашей работы!; Нарушение авторских прав |