
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Кривые безразличия и выбор «лучшего портфеля».
Метод, который будет применен для выбора наиболее желательного портфеля, использует так называемые кривые безразличия. Эти кривые отражают отношение инвестора к риску и доходности и, таким образом могут быть представлены как двухмерный график, где по горизонтальной оси откладывается риск, мерой которого является стандартное отклонение (обозначается σр ), а по вертикальной оси вознаграждение, мерой которого является ожидаемая доходность (обозначенная rр).
|
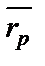 I2 I2
I1 X
I1
I2
σp Рисунок 7.2 Пересекающиеся кривые безразличия. |
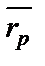 I2 I2
I* I1
σp Рисунок 7.3. Построение третьей кривой безразличия. |
Второе свойство: инвестор будет считать любой портфель лежащий на кривой безразличия, которая находится выше и левее, более привлекательным, чем любой портфель на кривой безразличия, которая находиться ниже и правее. В заключение следует отметить, что инвестор имеет бесконечное число кривых безразличия. Это просто означает, что как бы не были расположены две кривые безразличия на графике, всегда существует возможность построить третью кривую, лежащую между ними. Как показано на рис.7.3., на котором заданы кривые безразличия I1и I2, можно построить третью кривую I*, лежащую между ними. Это также означает, что другая кривая безразличия может быть построена либо выше I2, либо ниже I1.
Из лекций
Эффективный портфель Марковица - портфель с самой высокой ожидаемой доходностью для данного уровня риска.
Согласно теории Г. Марковица, для принятия решения о вложении средств инвестору не нужно проводить оценку всех портфелей, а достаточно рассмотреть лишь так называемое эффективное множество портфелей и выбрать оптимальный.
Инвесторы, стремясь максимизировать ожидаемую доходность, одновременно желают минимизировать риск. Наличие этих противоречивых друг другу целей затрудняем принятие решения о приобретении ценных бумаг на начальном этапе, т.е. в момент времени t = 0.
Уменьшить влияние противоречивых друг другу целей рекомендуется с помощью покупки не одной, а нескольких бумаг, каждая из которых может отличаться не только доходностью, но и риском.
Если учесть, что портфель состоит из N числа разных по стоимости ценных бумаг, то уравнение доходности можно записать в виде
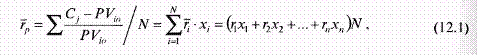
где р — среднеожидаемая доходность портфеля; х i — количество ценных бумаг i вида; r i — ожидаемая доходность ценной бумаги i вида; N — количество ценных бумаг в портфеле ( i = 1, 2, 3,... N ).
Согласно теории Г. Марковица, при обосновании портфеля инвестор должен руководствоваться ожидаемой доходностью и стандартным отклонением. Интуиция при этом играет определяющую роль. Ожидаемая доходность рассматривается как мера потенциального вознаграждения, связанная с конкретным портфелем, а стандартное отклонение — как мера риска, связанная с данным портфелем. При этом делается важное предположение, что инвестор при всех прочих условиях предпочтет высокую доходность, если будут заданы два портфеля с одинаковыми стандартными отклонениями. Если же инвестору предстоит выбор между портфелями, имеющими одинаковый уровень ожидаемой доходности, то предпочтение отдается портфелю с минимальным риском, т.е., по сути, получению большего дохода при минимуме возможного отклонения.
Принципы формирования инвестиционного портфеля (Г. Марковиц, 1952).
Выбор наиболее желаемого для инвестора портфеля определяется исходя кривых безразличия (изображают в системе «ожидаемая доходность – стандартное отклонение» предпочтения инвестора). 1 C s
r 2 rп
3 B
B H
A
12 A
E
11 C
8 А D
7 G
10 14 17 20 τ δ
Наиболее предпочтительные портфель С ( доходность 11%, отклонение 14%)
Выявить все возможные портфели
Выявить эффективное множество
Наложить кривую безразличия на это множества и выбрать оптимальный.
Дата добавления: 2015-04-18; просмотров: 252; Мы поможем в написании вашей работы!; Нарушение авторских прав |