Капиллярные явления.

Поместим цилиндрическую трубку малого сечения (капилляр) одним концом в жидкость, налитую в широкий сосуд (рис. 76).

Если жидкость частично смачивает капилляр, то ее поверхность в капилляре будет вогнутой сферической формы (рис. 76, а). При этом жидкость в капилляре поднимется на некоторую высоту h. Это можно объяснить тем, что давление на плоской поверхности жидкости, равное сумме атмосферного давления p₀и молекулярного давления p_Мбольше, чем давление p₀+p_М–2s/R на вогнутой поверхности мениска на величину давления Лапласа. Вследствие этой разности давлений жидкость в капилляре поднимется до такого уровня h, при котором гидростатическое давление столба жидкости rgh уравновесится давлением Лапласа p_Л=2s/R, где R – радиус сферы мениска, т. е.

.

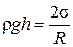Откуда

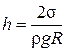. (5.5.1)

Как видно из рис. 76 радиус кривизны мениска R связан с радиусом капилляра r равенством R = r/cosq, где q – краевой угол. Учтя это, перепишем (5.5.1) в виде

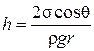. (5.5.2)

Если жидкость полностью смачивает твердое тело капилляра (к примеру, вода - чистое стекло), то q = 0и

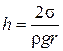. (5.5.3)

В этом случае сферическая поверхность мениска вписана во внутреннюю поверхность цилиндрического капилляра (R = r).

Если же жидкость частично не смачивает капилляр (рис.76, б), то давление на плоской поверхности жидкости, равное p₀ + p_М, будет меньше, чем давление p₀ +p_М=2s /R на выпуклой поверхности мениска, в результате чего жидкость в капилляре опустится на величину h, определяемую формулой (5.5.2). При этом h < 0, так как при частичном несмачивании краевой угол p2 £ q £ pи cosq <0.