Молекулярное давление и поверхностное натяжение жидкостей.

На каждую молекулу, находящуюся внутри жидкости, действуют силы притяжения со стороны всех молекул, расположенных в сфере действия этих сил. Как мы знаем, эта сфера имеет радиус . Равнодействующая всех сил 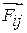, действующих на -ю молекулу со стороны молекул, находящихся в сфере радиуса , близка к нулю, т. е. .

Эта сила может быть точно равна нулю, если окружающие молекулы будут расположены совершенно симметрично и на равных расстояниях от нее. Однако случайное изменение в относительном расположении соседних молекул вследствие их теплового движения делает эту сумму отличной от нуля. Таким образом, каждая молекула жидкости все время движется под влиянием равнодействующей , меняющейся со временем по величине и направлению. Эта равнодействующая направлена в ту сторону, где случайно оказалась большая концентрация молекул и ближе расположены соседние молекулы. Следовательно, молекулярные силы взаимного притяжения способствуют концентрации молекул.

Пусть теперь j-я молекула расположена настолько близко к поверхности, что сфера молекулярного действия сил пересекает поверхность жидкости (рис.69, а).

а б

Р и с. 69

В этом случае часть сферы молекулярного действия сил, лежащая выше поверхности жидкости, содержит значительно меньше молекул жидкости (пар), чем расположенная ниже этой поверхности (жидкость), вследствие чего рассматриваемая молекула притягивается вниз сильнее, чем вверх. Поэтому равнодействующая не равна нулю и направлена вследствие симметрии перпендикулярно к поверхности внутрь жидкости.

Выберем на поверхности жидкости некоторую площадку S, к примеру, в форме круга (рис. 69, б). Молекулы, охваченные этой площадкой, связаны между собой внутренними силами, и поэтому этот мономолекулярный диск можно рассматривать как некоторое тело (пленку). Пусть на этой площадке вмещается N молекул. Тогда величина суммарной силы, действующей на все молекулы диска, будет равна

, (5.2.1)

так как все силы параллельны и имеют одну и ту же величину. Если величину (5.2.1) разделить на площадь S диска, то получим так называемое молекулярное давление p_Μ, с которым поверхностный слой действует на остальную массу жидкости:

. (5.2.2)

Каждый из сомножителей в последнем выражении пропорционален плотности жидкости ( − молярная масса, V_Μ − молярный объем). Поэтому

, (5.2.3)

где а − коэффициент пропорциональности, характеризующий силы притяжения между молекулами жидкости. Молекулярное давление в жидкости (5.2.3) имеет такой же вид, как для газов (3.4.8). Различие состоит только в величине молярного объема V_Μ, который для жидкостей значительно меньше, чем для газов. Оценим молекулярное давление для воды. Из опыта известно, что а = 0,555 Дж∙м³/моль², V_Μ = 18∙10^–3/10³ = 18∙10^–6 м³/моль. Подставляя эти величины в (5.2.3), получим

p_Μ = 1,7∙10⁹ Па 17000 атм.

Из приведенного примера ясно, почему жидкости трудно сжимаемы. Они всегда находятся в сжатом состоянии под очень высоким молекулярным давлением, и поэтому, заметное уменьшение объема требует приложения такого давления, которое было бы одного порядка с давлением молекулярным. Отметим, что непосредственно молекулярное давление измерить нельзя, так как любой манометр измеряет внешнее и гидростатическое давление.

Взаимное притяжение молекул вызывает не только давление поверхностного слоя на остальную жидкость, но стремится также уменьшить поверхность жидкости, т. е. вызывает силу, направленную вдоль поверхности, подобную той, какую мы имеем в натянутой резиновой пленке. Эта сила поверхностного натяжения тесно связана с молекулярным давлением. Действительно, каждая молекула, находящаяся на поверхности, испытывает силу, направленную внутрь жидкости, поэтому каждая такая молекула стремится уйти с поверхности и погрузиться в жидкость. Поэтому равновесие жидкости будет достигнуто при таком расположении молекул, когда на поверхности находится наименьшее возможное число молекул, т. е. поверхность жидкости имеет наименьшую величину. Это стремление жидкости иметь наименьшую поверхность создает сходство поверхности жидкости с упругой пленкой, которая, будучи растянута, стремится стянуться и уменьшить свою поверхность. Из всех тел данного объема наименьшую поверхность имеет шар. Поэтому мелкие капли жидкости принимают форму шара.

Рассмотрим снова мономолекулярный диск площадью S, расположенный на поверхности жидкости. На j-ю молекулу, лежащую внутри этого диска, действует веер сил , лежащих в плоскости, касательной к поверхности жидкости. Для всех молекул, расположенных внутри площадки S, все эти силы F_ij взаимно уравновешиваются. Только у молекул, расположенных вдоль окружности, ограничивающей площадку S, силы , направленные наружу, останутся неуравновешенными и дадут результирующую силу , перпендикулярную к окружности и касательную к поверхности жидкости. Сумма модулей этих внешних сил , растягивающих пленку, охватываемую площадкой S, называют силой поверхностного натяжения. Сила поверхностного натяжения, которая приходится на единицу длины окружности, ограничивающую площадку S, называется коэффициентом поверхностного натяжения данной жидкости:

. (5.2.4)

Единицей измерения коэффициента поверхностного натяжения в системе СИ является Н/м.

Коэффициент поверхностного натяжения зависит от температуры. С повышением температуры он уменьшается, так как при нагревании жидкости увеличивается среднее расстояние между молекулами, что приводит к уменьшению сил притяжения, а, значит, и результирующей силы F, действующей на единицу длины контура, расположенного на поверхности жидкости.

Используя формулу (5.2.4), можно ввести в рассмотрение другое, эквивалентное, определение коэффициента поверхностного натяжения. Для этого рассмотрим следующий опыт. Проволочный каркас заполним жидкой пленкой (рис. 70).

Р и с. 70

Перемычка СD каркаса может свободно скользить вдоль направляющих проволок АС и BD. Пленка состоит из нижней и верхней поверхностей, между которыми находится жидкость. На перемычку длины действует сила поверхностного натяжения . Чтобы перемычка находилась в равновесии, к ней нужно приложить силу . Под действием силы F₁ (точнее F₁ + dF₁) перемычка переместится на расстояние dx. При этом площадь поверхности пленки увеличится на величину . Увеличение поверхности пленки происходит за счет перехода молекул из глубины жидкости в поверхностный слой. При этом переходе молекулы расходуют свою кинетическую энергию на работу против силы R, направленной вовнутрь жидкости, уменьшая тем самым температуру жидкости. Чтобы температура жидкости не изменялась, перемычку необходимо перемещать бесконечно медленно. Тогда жидкость будет успевать получать теплоту от внешней среды и сохранять температуру постоянной.

Таким образом, работа силы F₁ + dF₁ при изотермическом увеличении площади поверхности жидкости на равна:

.

Откуда

. (5.2.5)

Из последнего выражения следует, что коэффициент поверхностного натяжения численно равен работе при изотермическом увеличении поверхности жидкости на единицу площади. Коэффициент 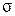является положительной величиной. Поэтому, если сила поверхностного натяжения жидкости совершает положительную работу , то перемычка движется так, что площадь поверхности жидкости уменьшается, т. е. , и тогда на основании (5.2.5) 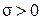. Наоборот, если внешняя сила F₁ совершает работу, то , и перемычка движется так, что площадь поверхности жидкости увеличивается, т. е. и снова .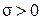

Мы знаем, что работа при обратимом изотермическом процессе равны убыли свободной энергии, т. е.

. (5.2.6)

Поэтому выражение (5.2.5) может быть записано в виде:

, (5.2.7)

т. е. коэффициент поверхностного натяжения численно равен изменению свободной энергии жидкости при увеличении площади ее поверхности на единицу. Выражение (5.2.7) является наиболее общим определением коэффициента поверхностного натяжения. Из этого выражения следует, что 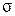можно также измерять в системе СИ в Дж/м² = Н/м.

Так как коэффициент поверхностного натяжения является функцией температуры жидкости и не зависит от ее площади, то из соотношения (5.2.7) следует, что

, (5.2.8)

т. е. свободная поверхностная энергия жидкости равна произведению 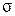на площадь поверхности S.

Учитывая, что работа, совершаемая пленкой, , основное уравнение термодинамики для обратимых процессов можно записать в виде

. (5.2.9)

Так как по определению свободная энергия , то

. (5.2.10)

Из соотношений (5.2.9–5.2.10) находим

. (5.2.11)

Отсюда

. (5.2.12)

Подставим в формулу для внутренней энергии выражения (5.2.8) и (5.2.12). В результате получим

. (5.2.13)

Так как коэффициент поверхностного натяжения является убывающей функцией температуры, то , и, как видно из (5.2.13), внутренняя энергия жидкости больше ее свободной поверхностной энергии, т. е. 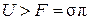. Это ясно, например, из того, что при приближении к критической точке, когда различие меж­ду жидкостью и газом исчезает, поверхностное натяжение должно стать равным нулю.

Теплота, получаемая жидкостью от внешней среды при образова­нии единицы площади поверхности пленки,

. (5.2.14)

Из последнего выражения видно, что , так как . Нетрудно видеть, что величина q меньше приращения энергии поверхности, так как (работа 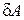отрицательна потому, что при увеличении площади поверхности работу совершает не пленка, а внешняя сила).