
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
И коэффициент температуропроводности при нормальных условиях
| Вещество |  , кг/м3 , кг/м3
| 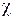 , Вт/м∙K , Вт/м∙K
| С, кДж/кг∙K | a∙106, м2/с |
| Окись углерода Воздух (сухой) Азот Кислород Латунь Олово Алюминий Медь Вода | 1,25 1,293 1,25 1,429 999,9 | 0,0233 0,0244 0,0243 0,0247 0,5513 | 1,039 1,005 1,03 0,915 0,377 0,221 0,921 0,381 4,212 | 17,9 18,8 18,9 18,9 33,8 41,1 86,7 112,5 0,131 |
При выводе уравнений (4.5.10–4.5.11) предполагалось, что поток тепла распространяется в одном направлении (вдоль оси X). Нетрудно обобщить эти уравнения на случай, когда температура в веществе изменяется в трех направлениях и зависит от времени, т. е. является функцией 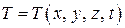 .
.
Для этого в веществе выделим элементарный параллелепипед с объемом dV = dx dy dz (рис. 62).

Р и с. 62
В этом случае температуры граней различны, поэтому теплота в параллелепипеде будет распространяться в направлении осей X, Y и Z.
Согласно закону Ж. Фурье (4.5.1), через грань dydz за время dt в объем dV втекает в направлении оси X количество теплоты
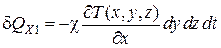 , (4.5.12)
, (4.5.12)
через противоположную грань из того же объема dV вытекает в том же направлении количество теплоты
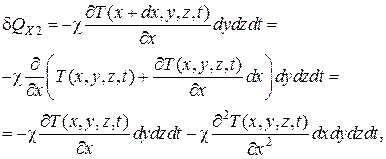 (4.5.13)
(4.5.13)
где  – температура второй грани, а величина
– температура второй грани, а величина 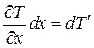 определяет приращение температуры в направлении оси X.
определяет приращение температуры в направлении оси X.
Так как макроскопическая работа не совершается, то приращение внутренней энергии вещества, находящегося в параллелепипеде, из-за движения теплоты в направлении оси X будет равно
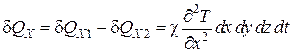 .(4.5.14)
.(4.5.14)
Совершенно аналогично приращения внутренней энергии в параллелепипеде в направлении осей X и Y представятся в виде
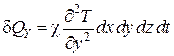 , (4.5.15)
, (4.5.15)
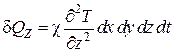 . (4.5.16)
. (4.5.16)
Суммарное приращение внутренней энергии вещества, находящегося в параллелепипеде, за время dt равно
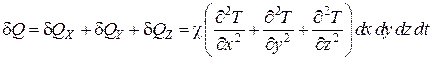 . (4.5.17)
. (4.5.17)
С другой стороны, согласно закону сохранения энергии, количество тепла, поступившего в параллелепипед, идет на приращение внутренней энергии вещества и, как следствие, на повышение его температуры:
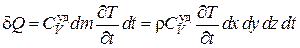 , (4.5.18)
, (4.5.18)
где 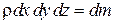 – масса вещества в параллелепипеде,
– масса вещества в параллелепипеде, 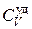 – удельная теплоемкость при постоянном объеме,
– удельная теплоемкость при постоянном объеме, 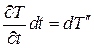 – приращение температуры во времени (за время dt).
– приращение температуры во времени (за время dt).
Так как левые части выражений (4.5.17) и (4.5.18) равны, то и правые равны, т. е.
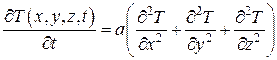 , (4.5.19)
, (4.5.19)
где 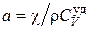 .
.
При выводе уравнения теплопроводности (4.5.19) предполагалось, что в произвольно выбранном элементарном параллелепипеде отсутствуют внутренние источники тепла. При наличии таких источников, необходимо к правой части уравнения (4.5.19) добавить величину qV, равную количеству тепла, поставляемого источниками в единицу объема вещества в единицу времени, разделенную на 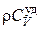 . Поэтому дифференциальное уравнение теплопроводности с источниками тепла внутри тела будет иметь вид
. Поэтому дифференциальное уравнение теплопроводности с источниками тепла внутри тела будет иметь вид
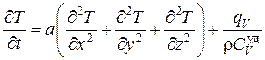 . (4.5.20)
. (4.5.20)
По существующей классификации дифференциальных уравнений с частными производными второго порядка уравнение теплопроводности является уравнением параболического типа (содержат первую производную по времени). Для решения этих уравнений необходимо располагать начальными и граничными условиями. Начальные условия предполагают, что в начальный момент t = 0 задано распределение температур в теле, т. е. задана функция 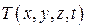 при t = 0. Граничные условия предполагают задание распределения температур на поверхности тела в любой момент времени. Кроме того, должны быть известны геометрическая форма и размеры тела, а также физические параметры окружающей среды и тела. Все эти условия называют краевыми. Решением уравнения теплопроводности с заданными краевыми условиями является функция
при t = 0. Граничные условия предполагают задание распределения температур на поверхности тела в любой момент времени. Кроме того, должны быть известны геометрическая форма и размеры тела, а также физические параметры окружающей среды и тела. Все эти условия называют краевыми. Решением уравнения теплопроводности с заданными краевыми условиями является функция 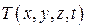 , которая определяет температурное поле во всем объеме тела для любого момента времени. Решение большинства реальных задач находят численными методами с использованием вычислительных машин.
, которая определяет температурное поле во всем объеме тела для любого момента времени. Решение большинства реальных задач находят численными методами с использованием вычислительных машин.
В качестве примера рассмотрим простейший, но широко распространенный случай – теплопроводность через однослойную плоскую стенку, длина и ширина которой велики по сравнению с толщиной d (рис. 63).

Р и с. 63
Это может быть бетонная или кирпичная стена, отделяющая помещение, в котором поддерживается постоянная температура T1, от внешней среды, находящейся при другой температуре T2. Температура изменяется только в направлении, перпендикулярном к плоскости стенки, которое примем за ось X. При стационарном (установившемся) тепловом режиме температура в любой плоскости, параллельной внешним плоскостям стенки и проходящей через любую внутреннюю точку стенки, постоянна и не зависит от времени, т. е. 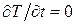 . Так как в направлении осей Y и Zтемпература не меняется, то
. Так как в направлении осей Y и Zтемпература не меняется, то 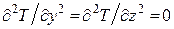 . При таких условиях уравнение теплопроводности (4.5.19) принимает вид:
. При таких условиях уравнение теплопроводности (4.5.19) принимает вид:
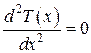 . (4.5.21)
. (4.5.21)
Откуда находим
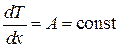 .
.
Второе интегрирование дает
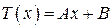 . (4.5.22)
. (4.5.22)
Постоянные A и B могут быть найдены из граничных условий. При x = 0 T(0) = T1 = B; при x = d T(d) = Ad + T1 = T2 и, таким образом, A = (T2 –T1)/d.
Подставив найденные постоянные коэффициенты в уравнение прямой (4.5.22), получим
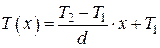 . (4.5.23)
. (4.5.23)
Плотность теплового потока q найдем по формуле (4.5.3):
 . (4.5.24)
. (4.5.24)
Следует заметить, что тепловой поток зависит не от абсолютного значения температур, а от их разности.
Количество тепла, проходящее через площадь S стенки за время t, на основании формулы (4.5.1), равно:
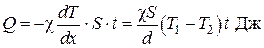 . (4.5.25)
. (4.5.25)
Это количество теплоты прямо пропорционально коэффициенту теплопроводности стенки, ее площади S, промежутку времени t, разности температур на внешних сторонах стенки 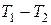 и обратно пропорционально толщине стенки d.
и обратно пропорционально толщине стенки d.
Вычисление и опытное определение коэффициента теплопроводности
Как отмечалось ранее, переносимой величиной при теплопроводности является средняя кинетическая энергия молекулы, т. е.
 . (4.6.1)
. (4.6.1)
Проделаем очевидные преобразования с правой частью (4.6.1)
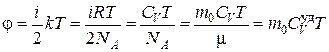 , (4.6.2)
, (4.6.2)
где 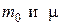 – масса молекулы и молярная масса соответственно.
– масса молекулы и молярная масса соответственно.
Подставляя (4.6.2) в (4.4.7), получим
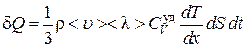 , (4.6.3)
, (4.6.3)
где 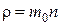 – плотность газа.
– плотность газа.
Сравнивая последнее выражение с (4.5.1), находим
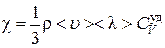 . (4.6.4)
. (4.6.4)
Из последнего соотношения видно, что коэффициент теплопроводности 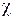 не зависит от давления, так как плотность газа прямо пропорциональна давлению, а средняя длина свободного пробега обратно пропорциональна давлению; средняя же скорость молекул
не зависит от давления, так как плотность газа прямо пропорциональна давлению, а средняя длина свободного пробега обратно пропорциональна давлению; средняя же скорость молекул 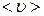 и удельная теплоемкость газа не зависят от давления. Это можно объяснить следующим образом. Чем выше давление газа, тем больше его плотность и, следовательно, тем больше молекул участвует в переносе их кинетической энергии, но при этом они проходят меньшее расстояние между соударениями.
и удельная теплоемкость газа не зависят от давления. Это можно объяснить следующим образом. Чем выше давление газа, тем больше его плотность и, следовательно, тем больше молекул участвует в переносе их кинетической энергии, но при этом они проходят меньшее расстояние между соударениями.
При постоянной плотности идеального газа в выражении (4.6.4) только средняя скорость зависит (как  ) от температуры. Поэтому коэффициент теплопроводности идеального газа растет пропорционально
) от температуры. Поэтому коэффициент теплопроводности идеального газа растет пропорционально  . Однако опыт показывает, что
. Однако опыт показывает, что 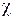 растет с увеличением температуры несколько быстрее, чем
растет с увеличением температуры несколько быстрее, чем  , и притом неодинаково для разных газов. Объясняется это тем, что при постоянной плотности газа при повышении его температуры увеличивается средняя длина свободного пробега из-за уменьшения эффективного диаметра молекул (см. введение), а также растет удельная теплоемкость реального газа.
, и притом неодинаково для разных газов. Объясняется это тем, что при постоянной плотности газа при повышении его температуры увеличивается средняя длина свободного пробега из-за уменьшения эффективного диаметра молекул (см. введение), а также растет удельная теплоемкость реального газа.
Для определения коэффициента теплопроводности чаще всего употребляется следующая экспериментальная установка. Исследуемым газом заполняется пространство между двумя коаксиальными цилиндрами с радиусами R1 и R2, при этом внутренним цилиндром служит проволока (подвешенная с грузом для ее натяжения), по которой пропускают ток, выделяющий в единицу времени энергию 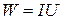 (I – ток, U – напряжение). При установившемся (стационарном) режиме температура проволоки T1 постоянна и выше температуры T2 внешнего цилиндра, находящегося в термостате. Тогда, согласно закону Фурье, количество тепла, проходящего в единицу времени через произвольную цилиндрическую поверхность площади
(I – ток, U – напряжение). При установившемся (стационарном) режиме температура проволоки T1 постоянна и выше температуры T2 внешнего цилиндра, находящегося в термостате. Тогда, согласно закону Фурье, количество тепла, проходящего в единицу времени через произвольную цилиндрическую поверхность площади 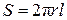 (r – радиус цилиндра, l – его длина), равно
(r – радиус цилиндра, l – его длина), равно
 . (4.6.5)
. (4.6.5)
В стационарном состоянии 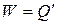 . Поэтому
. Поэтому
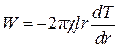 . (4.6.6)
. (4.6.6)
Откуда находим
 . (4.6.7)
. (4.6.7)
Интегрируя левую часть (4.6.7) в пределах от T1 до T2, а правую – от R1 до R2, получим
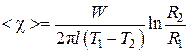 , (4.6.8)
, (4.6.8)
где –среднее значение коэффициента теплопроводности на интервале (T1, T2). Измерив величины I, U, R1, R2, l, T1 и T2 можно вычислить коэффициент
–среднее значение коэффициента теплопроводности на интервале (T1, T2). Измерив величины I, U, R1, R2, l, T1 и T2 можно вычислить коэффициент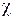 .
.
61. Внутреннее трение (вязкость) газов. Основной закон вязкости – закон Ньютона. Вычисление (и экспериментальное определение) коэффициента вязкости.
Явление внутреннего трения с макроскопической точки зрения связано с возникновением сил трения между слоями газа или жидкости, перемещающимися параллельно друг другу с различными по величине скоростями. Со стороны слоя, движущегося быстрее, на более медленно движущийся слой действует ускоряющая сила. Наоборот, медленно перемещающийся слой тормозит более быстро движущиеся слои газа. Силы трения, которые при этом возникают, направлены по касательной к поверхности соприкосновения слоев.
Рассмотрим известный опыт Ньютона. Пусть имеются две параллельные пластинки (рис. 64), между которыми находится газ (жидкость).
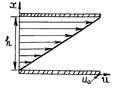
Р и с. 64
Расстояние между пластинками h. Нижнюю пластинку будем удерживать неподвижно, верхнюю заставим двигаться в одном и том же направлении в своей плоскости с постоянной скоростью u0.
Слой газа, непосредственно прилегающий к верхней пластинке, будет иметь ту же скорость u0, что и пластинка, слой же газа, прилегающий к нижней пластинке, находится в покое. Как показывает опыт, любой промежуточный слой движется со скоростью u, пропорциональной расстоянию x от неподвижной пластинки, т. е.
 . (4.7.1)
. (4.7.1)
Постоянная a определяется из условия, что при x = h u = u0, т. е.
u0 = ah. Откуда a = u0/h. Тогда выражение (4.7.1) примет вид
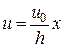 .(4.7.2)
.(4.7.2)
Таким образом, к верхней пластинке приложена сила F1, лежащая в ее плоскости и имеющая то же направление, что и направление движения пластинки. Так как пластинка движется с постоянной скоростью u0, то на пластинку должна действовать такая же по величине, но противоположно направленная сила F со стороны газа, которую назовем силой вязкого трения.
Из опыта следует, что абсолютная величина силы F1 пропорциональна скорости u0, с которой мы двигаем пластинку, и площади пластины, т. е.
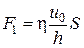 , (4.7.3)
, (4.7.3)
где  – постоянный коэффициент пропорциональности, который называют коэффициентом вязкого трения. Учитывая, что сила вязкого трения
– постоянный коэффициент пропорциональности, который называют коэффициентом вязкого трения. Учитывая, что сила вязкого трения 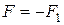 , равенство (4.7.3) перепишем в виде
, равенство (4.7.3) перепишем в виде
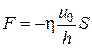 . (4.7.4)
. (4.7.4)
Так как из (4.7.2) следует, что  , то последнее выражение можно представить так:
, то последнее выражение можно представить так:
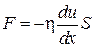 . (4.7.5)
. (4.7.5)
Это закон внутреннего вязкого трения Ньютона, который установил его экспериментально. Закон утверждает: при стационарном (ламинарном) движении слоев жидкости или газа с различными скоростями между ними возникают касательные силы, пропорциональные градиенту скорости слоев и площади их соприкосновения. Физический смысл коэффициента вязкости  заключается в том, что он численно равен силе, действующей на единицу площади поверхности, параллельной скорости течения газа или жидкости, при градиенте скорости
заключается в том, что он численно равен силе, действующей на единицу площади поверхности, параллельной скорости течения газа или жидкости, при градиенте скорости  .
.
Согласно второму закону Ньютона, 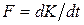 , где K – импульс элементарной массы слоя газа. Поэтому (4.7.5) можно представить в виде бесконечно малых:
, где K – импульс элементарной массы слоя газа. Поэтому (4.7.5) можно представить в виде бесконечно малых:
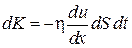 . (4.7.6)
. (4.7.6)
Пусть изменение скорости движения газа или жидкости происходит в направлении оси X, а сама скорость течения направлена перпендикулярно этой оси (рис. 65).
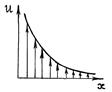
Р и с. 65
Тогда закон Ньютона (4.7.6) утверждает: импульс, переносимый за время dt через площадку dS, перпендикулярной оси X, пропорционален времени dt, величине площадки dS и градиенту скорости 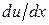 . Знак “минус” означает, что импульс переносится в направлении уменьшения скорости слоя.
. Знак “минус” означает, что импульс переносится в направлении уменьшения скорости слоя.
С молекулярно-кинетической точки зрения причиной внутреннего трения является наложение упорядоченного движения слоев газа с различными гидродинамическими скоростями u и хаотического теплового движения молекул. В результате теплового движения, молекулы из более быстрого слоя переносят с собой больший упорядоченный импульс 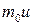 и, сталкиваясь, передают его молекулам более медленно движущегося слоя, вследствие чего он увеличивает скорость. Наоборот, при переходе молекул из медленно движущегося слоя в более быстрый слой, они приносят в него меньший упорядоченный импульс, что приводит к уменьшению упорядоченной скорости этого слоя. Увеличение или уменьшение гидродинамической скорости слоя газа, согласно второму закону динамики, свидетельствует о наличии силы внутреннего трения, действующей между слоями. Следовательно, за счет теплового хаотического движения скорости слоев будут выравниваться, если, конечно, внешними силами не поддерживать разности скоростей слоев.
и, сталкиваясь, передают его молекулам более медленно движущегося слоя, вследствие чего он увеличивает скорость. Наоборот, при переходе молекул из медленно движущегося слоя в более быстрый слой, они приносят в него меньший упорядоченный импульс, что приводит к уменьшению упорядоченной скорости этого слоя. Увеличение или уменьшение гидродинамической скорости слоя газа, согласно второму закону динамики, свидетельствует о наличии силы внутреннего трения, действующей между слоями. Следовательно, за счет теплового хаотического движения скорости слоев будут выравниваться, если, конечно, внешними силами не поддерживать разности скоростей слоев.
Таким образом, с точки зрения молекулярно-кинетической теории в процесс внутреннего трения каждая молекула переносит упорядоченный импульс 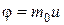 , вызывая тем самым изменение импульса слоя. Подставляя в общее уравнение переноса (4.4.7)
, вызывая тем самым изменение импульса слоя. Подставляя в общее уравнение переноса (4.4.7) 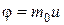 и
и 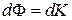 , получим:
, получим:
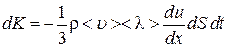 . (4.7.7)
. (4.7.7)
Сравнивая последнее соотношение с (4.7.6), получим формулу для коэффициента вязкости газов:
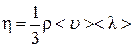 . (4.7.8)
. (4.7.8)
Из формулы (4.7.8) видно, что коэффициент вязкости газов, как и коэффициент теплопроводности, не зависит от давления. Опыт подтверждает этот вывод. Отклонения наблюдаются при очень низких и очень высоких давлениях, когда  начинает зависеть от давления. Зависимость
начинает зависеть от давления. Зависимость  от температуры такая же, как для коэффициента теплопроводности.
от температуры такая же, как для коэффициента теплопроводности.
Наиболее точные методы измерения коэффициента вязкости основаны на формуле Пуазейля:
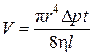 , (4.7.9)
, (4.7.9)
где V – объем газа, протекшего за время t через капилляр радиуса r и длины l при разности давлений 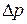 на его концах. Измерив в опыте все указанные величины, из формулы Пуазейля находят коэффициент вязкости
на его концах. Измерив в опыте все указанные величины, из формулы Пуазейля находят коэффициент вязкости  .
.
62. Диффузия. Основной закон диффузии – закон Фика. Вычисление коэффициента самодиффузии газов.
Диффузией называют неравновесный процесс самопроизвольного взаимного проникновения и перемешивания двух или более различных веществ. В смеси газов причиной диффузии является различие в концентрациях отдельных компонентов газов в разных частях объема. При этом каждый из компонентов смеси направленно переносится из тех частей объема, где ее концентрация больше, туда, где она меньше.
Газовую смесь будем считать бинарной, т. е. состоящей из двух компонентов 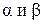 . Пусть общее число молекул в смеси равно N. Из них
. Пусть общее число молекул в смеси равно N. Из них 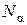 молекул компоненты
молекул компоненты 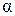 и
и 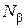 молекул компоненты
молекул компоненты 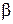 , т. е.
, т. е.
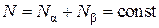 .(4.8.1)
.(4.8.1)
Разделив последнее равенство на объем V, занятый смесью, получим аналогичное соотношение для концентраций:
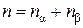 .(4.8.2)
.(4.8.2)
Давление и температура газовой смеси при диффузии постоянны во всех частях объема. Если бы, к примеру, температура не была в разных частях объема постоянной, то процесс теплопроводности накладывался бы на процесс диффузии. Мы же намерены рассмотреть процесс диффузии без других сопровождающих его процессов.
Для идеального газа 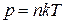 . Тогда из условия постоянства давления и температуры следует, что n = const, т. е.
. Тогда из условия постоянства давления и температуры следует, что n = const, т. е.
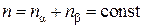 . (4.8.3)
. (4.8.3)
Будем решать задачу диффузии в предположении, что концентрации компонентов являются функциями одной переменной x, т. е. концентрации компонентов 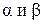 в газе меняются только вдоль оси X. Тогда, продифференцировав равенство (4.8.3), получим
в газе меняются только вдоль оси X. Тогда, продифференцировав равенство (4.8.3), получим
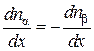 .(4.8.4)
.(4.8.4)
Отсюда следует, что при рассмотрении процесса диффузии в одномерном случае скорость роста концентрации одной из компонент в направлении оси X должна быть равна скорости убыли концентрации другой в том же направлении (рис.66).
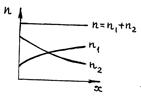
Р и с. 66
Только в этом случае общая концентрация смеси при любом значении х будет постоянна, т. е.  , и
, и 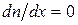 .
.
Опытным путем установлено (первый закон Фика), что число молекул dN 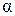 компоненты
компоненты 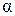 , продиффундировавших через площадку dS за время dt, пропорционально величине площадки dS, промежутку времени dt и градиенту концентрации
, продиффундировавших через площадку dS за время dt, пропорционально величине площадки dS, промежутку времени dt и градиенту концентрации 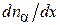 этого компонента, т. е.
этого компонента, т. е.
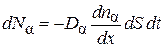 ,(4.8.5)
,(4.8.5)
где Da – коэффициент диффузии компонента 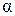 , который, как видно из
, который, как видно из
(4.8.5), имеет размерность в системе СИ м2/с и численно равен числу молекул компонента 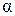 , переносимых через единичную площадку в единицу времени при градиенте концентрации компонента
, переносимых через единичную площадку в единицу времени при градиенте концентрации компонента 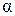
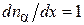 . Знак “минус” в законе Фика указывается, что процесс диффузии направлен всегда в сторону уменьшения концентрации молекул.
. Знак “минус” в законе Фика указывается, что процесс диффузии направлен всегда в сторону уменьшения концентрации молекул.
Уравнение Фика для второго компонента газовой смеси имеет точно такой же вид:
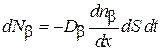 .(4.8.6)
.(4.8.6)
Нетрудно показать, что 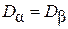 . В самом деле, из выражения (4.8.1) следует, что
. В самом деле, из выражения (4.8.1) следует, что
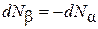 .(4.8.7)
.(4.8.7)
Подставив (4.8.7) и (4.8.4) в (4.8.6), получим
 .(4.8.8)
.(4.8.8)
Сравнивая последнее выражение с (4.8.5), заключаем, что коэффициенты диффузии компонент 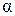 и
и 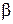 равны, т. е.
равны, т. е. 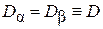 .
.
Умножив (4.8.5) на массу 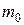 молекулы, получим выражение для количества массы
молекулы, получим выражение для количества массы 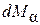 , переносимой через площадку dS за время dt:
, переносимой через площадку dS за время dt:
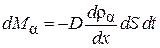 ,(4.8.9)
,(4.8.9)
где 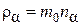 – парциальная плотность компонента
– парциальная плотность компонента 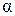 .
.
Закон Фика справедлив для веществ, находящихся в любых агрегатных состояниях. Различие заключается в величине коэффициента диффузии (см. таблицу 4.8.1).
Таблица 4.8.1
| Диффундирующее вещество | Основной компонент | Температура,  С С
| D, м2/с |
| Водород (газ) | Кислород (газ) | 0,70×10-4 | |
| Пары воды | Воздух | 0,23×10-4 | |
| Поваренная соль | Вода | 1,1×10-9 | |
| Золото (твердое) | Свинец (твердый) | 4×10-14 | |
| Свине (твердый) | Свинец (твердый) | 7×10-15 |
Если выражения (4.8.5) и (4.8.9) разделить на dSdt , то число молекул компонента 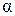 , диффундирующих через единичную площадку в единицу времени
, диффундирующих через единичную площадку в единицу времени
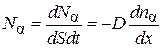 ,(4.8.10)
,(4.8.10)
масса же компонента 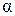 , переносимая через единичную площадку в единицу времени
, переносимая через единичную площадку в единицу времени
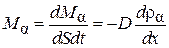 .(4.8.11)
.(4.8.11)
Величину Na (или Ma) называют диффузионным потоком компонента 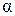
Пусть в одной из половин сосуда, разделенном перегородкой, находится азот, в другой – кислород. Если убрать перегородку, то начнется нестационарный процесс диффузии газов, который приведет к выравниванию концентраций обоих компонентов по всему сосуду. Зафиксируем координату х так, чтобы она находилась в той половине сосуда, где находится азот. Тогда концентрация азота в этой точке со временем будет уменьшаться, будет уменьшаться и диффузионный поток. Это означает, что диффузионный поток при нестационарной диффузии является функцией не только координаты х, но и времени t, т. е. 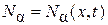 .
.
Выведем дифференциальное уравнение, которому удовлетворяет концентрация диффузионного компонента при нестационарной одномерной диффузии. Для этого в бинарной смеси газов выделим элементарный параллелепипед с площадью основания dS и высотой dx (рис. 67).
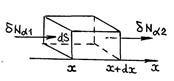
Р и с.67
Число молекул компоненты 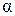 , входящих в параллелепипед за время dt через основание с координатой x,
, входящих в параллелепипед за время dt через основание с координатой x,
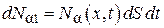 ,(4.8.12)
,(4.8.12)
а уходящее через основание с координатой x + dx за то же время
 .(4.8.13)
.(4.8.13)
Следовательно, число частиц поступивших в параллелепипед за время dt
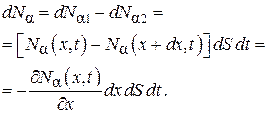 (4.8.14)
(4.8.14)
С другой стороны, приход этих молекул в элементарный объем  увеличивает их концентрацию в этом объеме на величину
увеличивает их концентрацию в этом объеме на величину
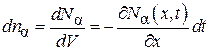 .(4.8.15)
.(4.8.15)
Откуда находим
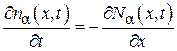 .(4.8.16)
.(4.8.16)
Так как коэффициент диффузии D зависит только от температуры, то, подставив выражение (4.8.10) в (4.8.16), получим
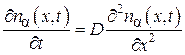 .(4.8.17)
.(4.8.17)
Уравнение (4.8.17) является дифференциальным уравнением диффузии (второй закон Фика) для случая, если концентрация компонента 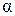 изменяется только в направлении оси X. В общем случае, когда концентрация nα является функцией трех пространственных координат и времени, нетрудно вывести уравнение диффузии методом, которым мы получили уравнение теплопроводности (4.5.19). Это уравнение имеет вид:
изменяется только в направлении оси X. В общем случае, когда концентрация nα является функцией трех пространственных координат и времени, нетрудно вывести уравнение диффузии методом, которым мы получили уравнение теплопроводности (4.5.19). Это уравнение имеет вид:
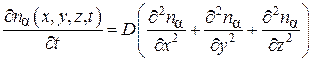 .(4.8.18)
.(4.8.18)
Уравнение диффузии (4.8.18) имеет такой же вид, как уравнение теплопроводности (4.5.19), только в уравнении диффузии содержится коэффициент диффузии D, а в уравнении теплопроводности − коэффициент температуропроводности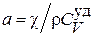 .
.
Вычислим коэффициент диффузии, воспользовавшись общим уравнением явлений переноса (4.4.7). Переносимой величиной 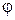 в процессе диффузии является концентрация компоненты
в процессе диффузии является концентрация компоненты 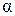 , рассчитанная на одну молекулу смеси, т. е.
, рассчитанная на одну молекулу смеси, т. е.
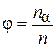 .(4.8.19)
.(4.8.19)
Подставляя последнее соотношение в (4.4.7) и заменяя 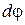 на
на 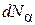 , получим
, получим
 .(4.8.20)
.(4.8.20)
Сравнение последнего выражения с (4.8.5) дает
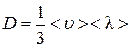 .(4.8.21)
.(4.8.21)
Из последнего соотношения видно, что процесс взаимного проникновения и перемешивания газов идет тем интенсивнее, чем больше средняяскорость и средняя длина свободного пробега молекул.
Из формул (1.11.7) и (4.1.10) видно, что при заданной температуре средняя скорость молекул не зависит от давления, а средняя длина их свободного пробега обратно пропорциональна давлению. Поэтому
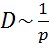 ,(4.8.21)
,(4.8.21)
что подтверждается опытом. Из тех же формул следует, что средняя скорость молекул прямо пропорциональна 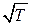 , а средняя длина свободного пробега при постоянной концентрации
, а средняя длина свободного пробега при постоянной концентрации 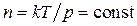 не зависит от температуры. Следовательно, коэффициент диффузии
не зависит от температуры. Следовательно, коэффициент диффузии
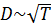 .(4.8.22)
.(4.8.22)
Формула (4.8.20) справедлива в том случае, если молекулы компонентов 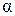 и
и 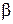 смеси сравнимы по своим массам и размерам. При большом различии между ними, как показывают более детальные теории, коэффициент диффузии для бинарной смеси определяется по формуле:
смеси сравнимы по своим массам и размерам. При большом различии между ними, как показывают более детальные теории, коэффициент диффузии для бинарной смеси определяется по формуле:
 .(4.8.23)
.(4.8.23)
где d12=(d1+d2)/2– средний диаметр молекул, m – их приведенная масса, равная m1m2/(m1+m2).
Между коэффициентами переноса существуют простые зависимости, вытекающие из формул (4.6.4), (4.7.8) и (4.8.20):
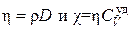 .(4.8.24)
.(4.8.24)
Из последних формул следует, что измеренный на опыте один из коэффициентов переноса позволяет находить два других.
Определив из опыта коэффициент вязкого трения 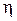 (или
(или 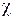 ) можно вычислить эффективный диаметр молекулы. В самом деле, из формулы (4.7.8) средняя длина свободного пробега
) можно вычислить эффективный диаметр молекулы. В самом деле, из формулы (4.7.8) средняя длина свободного пробега
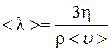 .(4.8.25)
.(4.8.25)
С другой стороны, из формулы (4.1.9)
 .(4.8.26)
.(4.8.26)
Из соотношений (4.8.25–4.8.26) находим
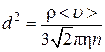 .(4.8.27)
.(4.8.27)
Это наиболее точный метод определения эффективного диаметра молекул.
Некоторые свойства разреженных газов. Физические явления в сильно разреженных газах. Определение вакуума. Течение и равновесие газов в условиях вакуума. Молекулярное течение. Тепловая эффузия.
Как мы знаем, средняя длина свободного пробега молекул
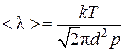 ,(4.9.1)
,(4.9.1)
и, таким образом, обратно пропорциональна давлению газа. При достаточно низком давлении средняя длина свободного пробега молекул может сравниться либо существенно превысить характерные размеры h сосуда. В зависимости от величины отношения 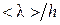 различают низкий (
различают низкий ( 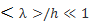 ), средний (
), средний ( 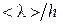
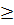 1) и высокий (
1) и высокий (  ) вакуум. Физические явления в среднем и высоком вакууме обладают интересными особенностями.
) вакуум. Физические явления в среднем и высоком вакууме обладают интересными особенностями.
Пусть газ находится в сосуде в условиях высокого вакуума. Сосуд разделен на две части A и В перегородкой, имеющей отверстие площади S. Температуры газа по обе стороны перегородки одинаковы (ТА = ТВ), а давления разные (для определенности pA > pB). Через отверстие будут наблюдаться два противоположно направленных потока несталкивающихся между собой молекул (при высоком вакууме молекулы сталкиваются практически только со стенками сосуда). Согласно формуле (1.4.12), число молекул, проходящих в единицу времени через отверстие площадью S из части A в часть B сосуда,
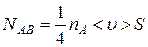 ,(4.9.2)
,(4.9.2)
а в противоположном направлении –
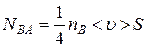 ,(4.9.3)
,(4.9.3)
где
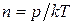 ,(4.9.4)
,(4.9.4)
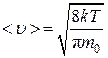 .(4.9.5)
.(4.9.5)
Результирующее число молекул, пролетающих в единицу времени через отверстие площади S, из A в В
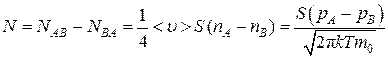 .(4.9.6)
.(4.9.6)
Если два сосуда A и B соединены цилиндрической трубкой радиусом r и длиной l, то, как показал М. Кнудсен, результирующий поток будет равен:
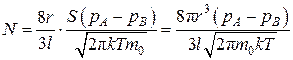 .(4.9.7)
.(4.9.7)
При получении формул (4.9.6–4.9.7) предполагалось, что 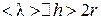 , где h – характерный размер сосуда.
, где h – характерный размер сосуда.
Если же, наоборот, давление газа настолько велико, что средняя длина свободного пробега молекул значительно меньше диаметра отверстия,
т. е. 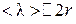 , то истечение газа происходит по закону Пуазейля, согласно которому объем газа, протекающего в единицу времени через трубку радиусом r и длиной l,
, то истечение газа происходит по закону Пуазейля, согласно которому объем газа, протекающего в единицу времени через трубку радиусом r и длиной l,
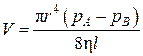 ,(4.9.8)
,(4.9.8)
где (pA − pB) – разность давлений на концах трубы,  – вязкость газа. В этом случае число молекул, проходящих в единицу времени через трубу
– вязкость газа. В этом случае число молекул, проходящих в единицу времени через трубу
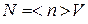 ,(4.9.9)
,(4.9.9)
где < n > – среднее число молекул в единице объема газа в трубе, равное
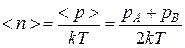 .(4.9.10)
.(4.9.10)
Подставим выражения (4.9.8) и (4.9.10) в (4.9.9), в результате будем иметь
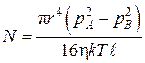 .(4.9.11)
.(4.9.11)
Соотношение Пуазейля (4.9.11), описывающее истечение газа через отверстие, размеры которого значительно больше средней длины свободного пробега молекул, является следствием законов гидродинамики и потому справедливо для сплошных сред. В этом случае молекулы вблизи отверстия многократно сталкиваются друг с другом, и число молекул, попадающих в отверстие, не равно числу молекул, пролетающих через него. В результате столкновений молекул возникнет упорядоченное движение газа через отверстие.
Формула Кнудсена (4.9.7), описывающая вытекание разреженного газа через маленькое отверстие (эффузия), размеры которого малы по сравнению со средней длиной свободного пробега молекул, справедлива только для сильно разряженных газов. При эффузии молекулы газа, двигаясь хаотически, покидают сосуд А независимо одна от другой, проходя через отверстие с такой же скоростью, которую они имели на значительном расстоянии отверстия. Поэтому при эффузии нет упорядоченного движения газа.
Как видно из формулы (4.9.7), скорость N эффузии уменьшается с ростом массы m0 молекулы. Поэтому при эффузии смеси двух газов с разными массами вытекающий газ будет содержать больше молекул легкого компонента. Пропуская смесь газов через специально изготовленные пористые перегородки, имеющие множество малых отверстий (капилляров), получают смесь, обогащенную легким компонентом. Повторяя этот процесс многократно удается выделить практически чистый легкий компонент газа.
Особенно широко применяется процесс эффузии при промышленном разделении изотопов (атомов с совершенно одинаковыми химическими свойствами, но с разными массами) одних и тех же химических элементов. Химическим способом такие смеси разделить невозможно.
Предположим теперь, что разреженный газ в частях А и В сосуда, разделенных перегородкой с малым отверстием, имеет одинаковые давления (pA = pB), но разные температуры (TA>TB). Из равенства давлений следует, что nAkTA = nB kTB, откуда
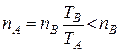 ,(4.9.12)
,(4.9.12)
так как TB < TA. Таким образом, при равенстве давлений концентрация молекул в части В больше концентрации в части А сосуда. Если температуры поддерживаются постоянными в разных частях сосуда, то в плотных газах при равенстве давлений с одной и c другой стороны отверстия (механическое равновесие) не вызовет преимущественного потока молекул через это отверстие. В разреженных же газах понятие давления на отверстие с разных сторон теряет смысл, так как молекулы свободно проходят через отверстие, не сталкиваясь друг с другом. Поэтому разная концентрация (nA < nB) с обеих сторон отверстия приведет к возникновению преимущественного потока молекул в ту сторону, где температура выше, т. е. из B в A. В результате вырастет концентрация молекул в части A сосуда и, следовательно, увеличится поток молекул из A в B. В конце концов, наступит момент, когда потоки через отверстие с противоположных сторон станут одинаковыми:
 .(4.9.13)
.(4.9.13)
С учетом формул (4.9.4–4.9.5), последнее равенство можно представить в виде:
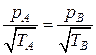 .(4.9.14)
.(4.9.14)
Таким образом, в сильно разреженных газах в обоих сосудах, разделенных малым отверстием, устанавливаются разные давления, причем в сосуде с более высокой температурой будет и более высокое давление. Этот процесс называют термоэффузией или эффектом Кнудсена.
Этот эффект играет важную роль во многих явлениях природы, в частности, с его помощью происходит обмен воздуха в почве, которая пронизана множеством капилляров диаметром в доли микрон. Легко подсчитать по формуле (4.9.1), что при атмосферном давлении средняя длина свободного пробега молекул воздуха порядка диаметра этих капилляров, т. е. воздух в капиллярах можно считать разреженным газом. Та часть воздуха в капилляре, которая расположена ближе к поверхности почвы, нагревается днем солнцем сильнее, чем часть воздуха, расположенного в глубине. В результате термоэффузии возникает поток воздуха в сторону большей температуры, т. е. к поверхности почвы, и рассеивается ветром. Ночью, наоборот, часть воздуха в капиллярах, расположенная ближе к поверхности почвы, остывает быстрее, чем в глубине и, благодаря этому, поток воздуха будет направлен от поверхности почвы в ее глубину. Таким образом в почве происходит обмен воздуха, необходимый для нормального роста растений.
Дата добавления: 2015-04-18; просмотров: 328; Мы поможем в написании вашей работы!; Нарушение авторских прав |