
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Эффект Джоуля-Томсона в газе Ван-дер-Ваальса.
Из уравнения Ван-дер-Ваальса

найдем производную

Так как –функция одной переменной
–функция одной переменной 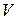 , то
, то
 .(3.9.1)
.(3.9.1)
Подставив выражение (3.9.1) в (3.8.15), получим
 .(3.9.2)
.(3.9.2)
Если выражение, стоящее в числителе формулы (3.9.2) равно нулю
 ,(3.9.3)
,(3.9.3)
то  и
и  т. е. газ Ван-дер-Ваальса в дроссель-эффекте не изменяет температуру.
т. е. газ Ван-дер-Ваальса в дроссель-эффекте не изменяет температуру.
Температуру, удовлетворяющую равенству (3.9.3), называют температурой инверсии и обозначают  :
:
 .(3.9.4)
.(3.9.4)
На рис. 55 представлена зависимость температуры инверсии  от молярного объема
от молярного объема 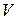 (кривая инверсии).
(кривая инверсии).

Р и с. 55
Любая точка на кривой инверсии с координатами (  ) определяет исходные (до проталкивания через дроссель) молярный объем
) определяет исходные (до проталкивания через дроссель) молярный объем 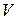 и температуру
и температуру  рабочего вещества. Следовательно, после просачивания вещества с такими начальными параметрами через дроссель его температура не изменится и останется равной
рабочего вещества. Следовательно, после просачивания вещества с такими начальными параметрами через дроссель его температура не изменится и останется равной  .
.
Если величина, стоящая в квадратной скобке формулы (3.9.2), больше нуля, что равносильно неравенству
 ,(3.9.5)
,(3.9.5)
то 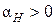 и
и  Это означает, если исходная температура рабочего вещества
Это означает, если исходная температура рабочего вещества  , то в дроссель-эффекте газ Ван-дер-Ваальса охлаждается, и, таким образом, всем точкам, расположенным ниже кривой инверсии отвечает положительный эффект Джоуля – Томсона (рис. 55).
, то в дроссель-эффекте газ Ван-дер-Ваальса охлаждается, и, таким образом, всем точкам, расположенным ниже кривой инверсии отвечает положительный эффект Джоуля – Томсона (рис. 55).
Наоборот, всем точкам расположенным выше кривой инверсии, начальная температура газа которых  , коэффициент Джоуля – Томсона
, коэффициент Джоуля – Томсона  и
и 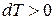 , т. е. газ Ван-дер-Ваальса при этом нагревается (отрицательный дроссель-эффект).
, т. е. газ Ван-дер-Ваальса при этом нагревается (отрицательный дроссель-эффект).
Если выполняется условие  т. е. объем, занимаемый самими молекулами, значительно меньше объема газа, то, как следует из формулы (3.9.4),
т. е. объем, занимаемый самими молекулами, значительно меньше объема газа, то, как следует из формулы (3.9.4),
 (3.9.6)
(3.9.6)
Из сравнения выражений для критической температуры  и температуры инверсии (3.9.6) следует, что
и температуры инверсии (3.9.6) следует, что
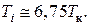 (3.9.7)
(3.9.7)
Из последнего соотношения видно, что температура инверсии для всех веществ значительно больше критической. Приведем экспериментальные значения температуры инверсии для некоторых веществ: для углекислого газа – 1500 К, для кислорода – 893 К, для азота – 621 К, для воздуха – 603 К, для водорода – 204 К, для гелия – 40 К.
Для всех газов, кроме водорода и гелия, температуры инверсии значительно выше комнатной температуры. Поэтому эти газы, взятые при исходной температуре, равной комнатной, будут всегда охлаждаться при дроссель-эффекте. У водорода и гелия температура инверсии намного меньше комнатной, поэтому они при дросселировании нагреваются. Следовательно, для получения положительного дроссель-эффекта (  ) необходимо предварительное глубокое охлаждение водорода и гелия.
) необходимо предварительное глубокое охлаждение водорода и гелия.
В заключение заметим, что процесс Джоуля – Томсона является существенно необратимым. В самом деле, из выражения (3.8.11) при  следует:
следует:
 (3.9.8)
(3.9.8)
Так как при дроссель-эффекте всегда 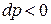 , то из последнего соотношения вытекает, что
, то из последнего соотношения вытекает, что  , что указывает на необратимость указанного процесса.
, что указывает на необратимость указанного процесса.
Дата добавления: 2015-04-18; просмотров: 1024; Мы поможем в написании вашей работы!; Нарушение авторских прав |