Внутренняя энергия газа Ван-дер-Ваальса. Адиабатическое расширения газа ВдВ в пустоту.

Выражение для внутренней энергии газа Ван-дер-Ваальса найдем следующим образом. При расширении газа его молекулы совершают работу 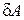против сил молекулярного давления . Эта работа равна

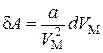,(3.7.1)

где – объем одного моля газа.

С другой стороны, эта работа идет на увеличение потенциальной энергии взаимодействия молекул:

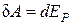.(3.7.2)

Из выражений (3.7.1–3.7.2) следует, что

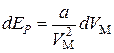.(3.7.3)

Интегрирование этого выражения дает

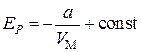.(3.7.4)

Внутренняя энергия 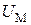газа состоит из кинетической 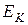и потенциальной 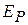энергий, т. е.

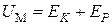.(3.7.5)

Подставим выражение (3.7.4) в (3.7.5).

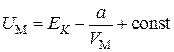.(3.7.6)

При 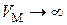газ становится идеальным и его внутренняя энергия равна кинетической энергии движения молекул 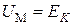и равна, как мы знаем, , т. е.

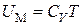.(3.7.7)

С другой стороны, при 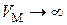из (3.7.6)

.(3.7.8)

Из сравнения выражений (3.7.7) и (3.7.8), заключаем, что 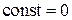. Таким образом, из (3.7.6)

.(3.7.9)

Внутренняя энергия 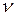молей газа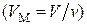

,(3.7.10)

где V – объем, занимаемый 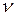молями газа.

Рассмотрим изотермическое расширение газа Ван-дер-Ваальса от объема 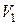до объема 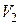. Изменение внутренней энергии на основании (3.7.10)

.(3.7.11)

Поэтому, согласно первому закону термодинамики, работа, произведенная газом Ван-дер-Ваальса при изотермическом расширении,

т. е. меньше количества полученного тепла, тогда как для идеального газа эта работа в точности равнялась количеству приобретенного тепла. Это объясняется тем, что в реальном газе при его изотермическом расширении часть тепла идет на работу против сил притяжения между молекулами, т. е. на увеличение потенциальной энергии молекул.

Рассмотрим далее адиабатное расширение газа Ван-дер-Ваальса без совершения внешней работы (так называемое расширение газа в вакуум). В этом случае в первом законе термодинамики необходимо положить 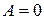и Тогда и т. е.

,

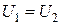и, учитывая выражение (3.7.10), последнее равенство можем переписать в виде:

.

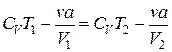Откуда находим

,

так как . Таким образом, газ Ван-дер-Ваальса при расширении в вакуум охлаждается. Охлаждение происходит потому, что в этом процессе часть кинетической энергии газа тратится на работу против сил притяжения между молекулами.