
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свободная энергия системы.
Ранее было установлено, что количество теплоты, получаемое системой в изохорном процессе  равно изменению ее внутренней энергии, т. е.
равно изменению ее внутренней энергии, т. е.
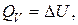 (2.16.1)
(2.16.1)
а в изобарном процессе это количество теплоты равно изменению энтальпии
 (2.16.2)
(2.16.2)
где энтальпия  . Изменение этих функций состояний (внутренней энергии и энтальпии) связано с тепловыми эффектами.
. Изменение этих функций состояний (внутренней энергии и энтальпии) связано с тепловыми эффектами.
Посмотрим теперь с какой функцией состояния связана работа, совершаемая системой. Для этого из основного уравнения термодинамики для обратимых процессов (2.14.3)
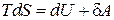 (2.16.3)
(2.16.3)
найдем работу, совершаемую системой в изотермическом процессе 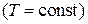
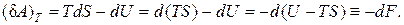 (2.16.4)
(2.16.4)
Величину 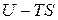 называют свободной энергией системы, которая является функцией состояния системы, т. к.
называют свободной энергией системы, которая является функцией состояния системы, т. к. 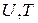 и
и 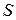 – функции состояния. Таким образом,
– функции состояния. Таким образом,
 (2.16.5)
(2.16.5)
или через энтальпию
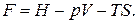 (2.16.6)
(2.16.6)
После интегрирования выражения (2.16.4), получаем
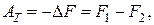 (2.16.7)
(2.16.7)
т. е. работа при обратимом изотермическом процессе равна убыли свободной энергии. При этом, чем больше энтропия 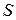 системы, тем меньше ее свободная энергия, тем меньше работа (2.16.7) и тем больше обесценена внутренняя энергия системы. Из выражения (2.16.5) находим
системы, тем меньше ее свободная энергия, тем меньше работа (2.16.7) и тем больше обесценена внутренняя энергия системы. Из выражения (2.16.5) находим
 (2.16.8)
(2.16.8)
т. е. внутренняя энергия состоит из двух частей: свободной энергии, которая при изотермических процессах расходуется на работу, и другой части 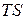 , которая выделяется в виде теплоты, и в работе не участвует. Часть
, которая выделяется в виде теплоты, и в работе не участвует. Часть 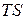 внутренней энергии называют связанной энергией.
внутренней энергии называют связанной энергией.
Из формулы (2.15.8), выражающей второй закон термодинамики для необратимых процессов, находим
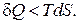
Подставив в первое начало термодинамики вместо 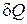 величину
величину 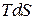 большую, чем
большую, чем 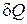 , получим
, получим
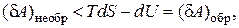 (2.16.9)
(2.16.9)
т. е. работа, совершаемая при необратимом процессе, всегда меньше, чем при обратимом.
В изотермических условиях неравенство (2.16.9) примет вид:
 (2.16.10)
(2.16.10)
Из неравенства (2.16.10) следует, что работа, производимая системой при необратимом изотермическом процессе, меньше убыли свободной энергии этой системы. Таким образом, 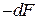 определяет максимальную работу, которую может произвести система в изотермическом процессе.
определяет максимальную работу, которую может произвести система в изотермическом процессе.
Статистическое толкование энтропии. Статистический смысл необратимости термодинамических процессов. Вероятности микросостояний и макросостояний идеального газа по пространственным положениям частиц. Биноминальное распределение вероятностей. Термодинамическая вероятность микросостояния. Равновесное состояние системы как наиболее вероятное. Связь энтропии и термодинамической вероятности состояния системы. Статистический характер 2-го начала термодинамики. Энтропия как мера беспорядка в системе.
Вышебыло показано, что в результате необратимого процесса, совершающегося в замкнутой системе, энтропия системы увеличивается, достигая своего максимального значения в состоянии равновесия. Обратный же процесс самопроизвольного перехода системы из равновесного состояния в исходное неравновесное состояние практически невозможен, т. к. обратный процесс протекал бы с уменьшением энтропии, что запрещено вторым законом термодинамики.
Такая односторонность в протекании необратимых процессов объясняется тем, что при достаточно большом числе молекул в системе вероятность равновесного состояния практически близка к единице, при этом сумма вероятностей всех других неравновесных состояний близка к нулю. Поэтому переход системы в наиболее вероятное (равновесное) состояние идет самопроизвольно, тогда как обратный процесс не может идти самопроизвольно от более вероятного (равновесного) состояния в сторону менее вероятных состояний.
Приведем пример. Пусть имеется сосуд, мысленно разделенный на два одинаковых объема  . В сосуде находится четыре молекулы. Чтобы различать состояния такого газа с микроскопической и макроскопической точек зрения, введем определения. Назовем микросостоянием газа по пространственным положениям частиц такое состояние, когда известно сколько молекул и с какими номерами находятся в каждой части сосуда (для этого необходимо заранее все четыре молекулы перенумеровать). Макроскопическим же назовем состояние, характеризуемое только числом молекул в различных частях сосуда.
. В сосуде находится четыре молекулы. Чтобы различать состояния такого газа с микроскопической и макроскопической точек зрения, введем определения. Назовем микросостоянием газа по пространственным положениям частиц такое состояние, когда известно сколько молекул и с какими номерами находятся в каждой части сосуда (для этого необходимо заранее все четыре молекулы перенумеровать). Макроскопическим же назовем состояние, характеризуемое только числом молекул в различных частях сосуда.
Так как каждая из молекул может находиться с равной вероятностью как в левой, так и в правой половине сосуда, то вероятность, что она находится в левой (или правой) части сосуда равна 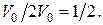 Поскольку вероятность пребывания каждой молекулы в левой (правой) половине не зависит от наличия в ней других, поэтому на основании теоремы умножения вероятностей, вероятность одновременного нахождения в левой части сосуда двух молекул равна
Поскольку вероятность пребывания каждой молекулы в левой (правой) половине не зависит от наличия в ней других, поэтому на основании теоремы умножения вероятностей, вероятность одновременного нахождения в левой части сосуда двух молекул равна 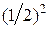 , трех –
, трех – 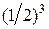 , четырех –
, четырех – 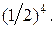
В табл. 2.17.1 приведены всевозможные микросостояния газа, вероятность каждого из которых, очевидно, равна 1/16. В пятой колонке табл. 2.17.1 также приведены значения статистического веса (статистическим весом или термодинамической вероятностью макросостояния называют число различных микросостояний, приводимых к данному макросостоянию). Так, например, статистический вес равновесного состояния газа (по две молекулы в левой и правой частях сосуда) равен 6, т. е. равновесному макроскопическому состоянию газа соответствует 6 различных микросостояний. Вероятность этого макроскопического состояния газа равна 4/16, что больше вероятности любых других макро-состояний. При увеличении числа молекул равновесное состояние реализуется большим числом микросостояний. Из таб. 2.17.1 также видно, что вероятность собраться молекулам в правой части сосуда равна 1/16 и реализуется одним микроскопическим состоянием. При увеличении числа молекул в сосуде вероятность такого неравновесного состояния становится малой. В 1 см3 воздуха при нормальных условиях содержится  молекул. Вероятность, что эти молекулы соберутся, например, в правой части сосуда, равна
молекул. Вероятность, что эти молекулы соберутся, например, в правой части сосуда, равна  , что является пренебрежимо малой величиной. Таким образом, если молекулы равномерно распределились по сосуду (равновесие), то вероятность того, что они вновь соберутся самопроизвольно в одной из половин сосуда (обратный процесс), практически является невозможным событием. Следует отме-тить, когда в сосуде наступит состояние равновесия, то это вовсе не означает, что число молекул в левой и правой частях сосуда в точности одинаково. В результате теплового, хаотического движения молекул число их, например, в левой части сосуда, будет непрерывно изменяться и только в среднем будет равно половине общего числа молекул, находящихся в сосуде. Мы знаем, что среднеквадратическое отклонение числа частиц в одной из частей сосуда от среднего (равновесного) значения пропорционально корню квадратному из числа частиц, т. е.
, что является пренебрежимо малой величиной. Таким образом, если молекулы равномерно распределились по сосуду (равновесие), то вероятность того, что они вновь соберутся самопроизвольно в одной из половин сосуда (обратный процесс), практически является невозможным событием. Следует отме-тить, когда в сосуде наступит состояние равновесия, то это вовсе не означает, что число молекул в левой и правой частях сосуда в точности одинаково. В результате теплового, хаотического движения молекул число их, например, в левой части сосуда, будет непрерывно изменяться и только в среднем будет равно половине общего числа молекул, находящихся в сосуде. Мы знаем, что среднеквадратическое отклонение числа частиц в одной из частей сосуда от среднего (равновесного) значения пропорционально корню квадратному из числа частиц, т. е.
 . (2.17.1)
. (2.17.1)
Допустим, что в сосуде находится всего лишь 200 молекул. Тогда в одной половине сосуда в среднем должно находиться 100 молекул. Согласно (2.17.1), отклонение от этого среднего количества cоставит:
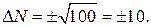
Это значит, что отклонение, как правило, не будет превышать 10 % среднего значения. Большое отклонение получилось потому, что число молекул в сосуде взято очень небольшим. Если в сосуде взять 20000 молекул, то 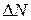 составит
составит  100 молекул, или 1 %.Если же число молекул в сосу-де взять равным
100 молекул, или 1 %.Если же число молекул в сосу-де взять равным 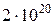 , то отклонение не превышало бы
, то отклонение не превышало бы  молекул, что составило бы всего лишь
молекул, что составило бы всего лишь  . В последнем случае отклонения от равномерного распределения были бы практически неощутимы.
. В последнем случае отклонения от равномерного распределения были бы практически неощутимы.
Таблица 2.17.1
| Макросостояние | Микросостояния | Статистичес-кий вес | Вероятность макросостояния | ||
| Число молекул слева | Число молекул справа | Номера молекул, находящихся в левой части сосуда | Номера молекул, находящихся в правой части сосуда | ||
| 1,2,3,4 | - | 1/16 | |||
| 1,2,3 1,2,4 1,3,4 2,3,4 | 4/16 | ||||
| 1,2 1,3 1,4 2,3 2,4 3,4 | 3,4 2,4 2,3 1,4 1,3 1,2 | 6/16 | |||
| 2,3,4 1,3,4 1,2,4 1,2,3 | 4/16 | ||||
| - | 1,2,3,4 | 1/16 | |||
| Всего микросостояний | 24 = 16 |
Теперь перейдем к рассмотрению общего случая. Пусть объем 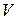 занимаемый газом разделен на
занимаемый газом разделен на 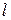 разных объемов
разных объемов 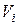 . Причем число ячеек
. Причем число ячеек 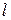 значительно меньше числа молекул
значительно меньше числа молекул 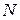 , т. е.
, т. е.  . Тогда в каждой ячейке будет находиться некоторое число молекул. Будем считать газ идеальным и, что внешние силовые поля отсутствуют. В этом случае вероятность того, что некоторая молекула будет обнаружена в i-й ячейке
. Тогда в каждой ячейке будет находиться некоторое число молекул. Будем считать газ идеальным и, что внешние силовые поля отсутствуют. В этом случае вероятность того, что некоторая молекула будет обнаружена в i-й ячейке 
Зафиксируем макросостояние, определяемое тем, что в первой ячейке находится 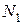 молекул, во второй ячейке –
молекул, во второй ячейке –  молекул,..., в l-й ячейке –
молекул,..., в l-й ячейке – 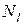 молекул (рис. 46).
молекул (рис. 46).

Р и с. 46
Ясно, что 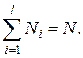 Число всевозможных перестановок среди
Число всевозможных перестановок среди 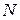 молекул равно
молекул равно 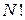 . Перестановки молекул в пределах каждой из ячеек не приводят к новому микросостоянию. Их следует исключить из общего числа перестановок. Если разделить
. Перестановки молекул в пределах каждой из ячеек не приводят к новому микросостоянию. Их следует исключить из общего числа перестановок. Если разделить 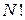 на
на  , то будут исключены те микросостояния, которые отличаются перестановками внутри первой ячейки. Полученный результат разделим на
, то будут исключены те микросостояния, которые отличаются перестановками внутри первой ячейки. Полученный результат разделим на 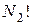 , что приведет к исключению тех микросостояний, которые отличаются перестановками во второй ячейке. Продолжив этот процесс деления, получим число различных микросостояний, которые приводят к данному макросостоянию, т. е. получим значение статистического веса (термодинамической вероятности) данного макросостояния:
, что приведет к исключению тех микросостояний, которые отличаются перестановками во второй ячейке. Продолжив этот процесс деления, получим число различных микросостояний, которые приводят к данному макросостоянию, т. е. получим значение статистического веса (термодинамической вероятности) данного макросостояния:
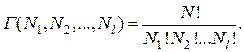 (2.17.2)
(2.17.2)
Все эти микросостояния равновероятны и вероятность каждого из них находится по теореме умножения вероятностей:
 (2.17.3)
(2.17.3)
Согласно теореме сложения несовместных событий, вероятность данного макросостояния равна сумме вероятностей микросостояний (2.17.3), число которых определяется выражением (2.17.2). Поэтому
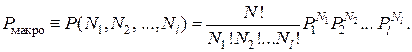 (2.17.4)
(2.17.4)
Если сосуд, в котором находится газ, разделен на l одинаковых
объемов 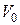 , то
, то 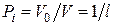 для всех
для всех 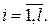 В этом случае формула (2.17.4) приобретает вид:
В этом случае формула (2.17.4) приобретает вид:
 (2.17.5)
(2.17.5)
Если же сосуд разделен только на два одинаковых объема, как это было в выше приведенном примере, то 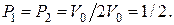 При этом формулы (2.17.2) и (2.17.5) упростятся:
При этом формулы (2.17.2) и (2.17.5) упростятся:
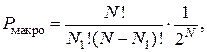 (2.17.6)
(2.17.6)
 (2.17.7)
(2.17.7)
Используя формулу (2.17.5), найдем вероятность того, что все молекулы соберутся в первой ячейке (N1 = N):
 (2.17.8)
(2.17.8)
Вероятность этого макросостояния является минимально возможной, так как ему соответствует только одно микросостояние:
 (2.17.9)
(2.17.9)
Наибольшим число микросостояний характеризуется равновесное состояние, т. е. когда молекулы равномерно распределены по объему 
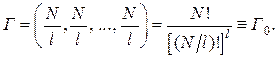 (2.17.10)
(2.17.10)
При этом и вероятность равновесного состояния будет наибольшей:
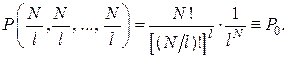 (2.17.11)
(2.17.11)
При больших 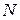 выражения (2.17.10–2.17.11) можно упростить, воспользовавшись формулой Стирлинга:
выражения (2.17.10–2.17.11) можно упростить, воспользовавшись формулой Стирлинга:
 и
и 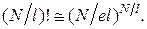 (2.17.12)
(2.17.12)
Подставив (2.17.12) в (2.17.10–2.17.11), будем иметь
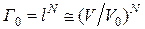 , (2.17.13)
, (2.17.13)
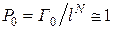 . (2.17.14)
. (2.17.14)
Таким образом, равновесное состояние реализуется с вероятностью близкой к единице, т. е. достоверно это состояние осуществляется наибольшим числом способов (микросостояний) 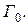 Поэтому в замкнутой системе происходят всегда такие процессы, которые приближают систему от менее вероятных состояний к более вероятным, т. е. равновесным состояниям, обратный же переход к неравновесному состоянию практически никогда не наблюдается, так как вероятность такого состояния мала.
Поэтому в замкнутой системе происходят всегда такие процессы, которые приближают систему от менее вероятных состояний к более вероятным, т. е. равновесным состояниям, обратный же переход к неравновесному состоянию практически никогда не наблюдается, так как вероятность такого состояния мала.
Экспериментальные изотермы. Критическая точка. Отклонение свойств реальных газов от идеальных. Конденсация газов. Критическое состояние вещества. Область двухфазных состояний вещества на диаграмме P-V. Фазовая диаграмма газ-жидкость.
Реальные газы отличаются от идеальных тем, что молекулы этих газов имеют конечные собственные объемы и связаны между собой сложными силами взаимодействия. При высоких давлениях и достаточно низких температурах реальные газы конденсируются, т. е. переходят в жидкое состояние, чего принципиально не может быть с идеальными газами.
В 1861 году ирландский физикохимик Т. Эндрюс экспериментально исследовал зависимость давления углекислого газа от объема при изотермическом сжатии. На рис. 47 схематично представлены результаты опытов, подобных опытам Т. Эндрюса. Рассмотрим изотерму АВСD.
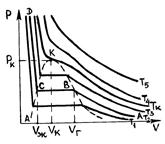
Р и с. 47
На участке АВ уменьшение объема, занятого газом, сопровождается увеличением давления сначала обратно пропорционально объему, затем все медленнее.
В точке В начинается конденсация газа и продолжается при постоянном давлении, называемом давлением насыщенных паров, до точки С. В точке С процесс конденсации газа заканчивается, при дальнейшем уменьшении объема осуществляется сжатие жидкости (участок СD), сопровождающееся быстрым ростом давления, свидетельствующее о том, что жидкость слабо сжимаема. При уменьшении давления, действующего на жидкость, вещество пройдет те же состояния в обратном порядке: оно расширится по пути DС до точки кипения, произойдет испарение (путь СВ), а затем получившийся пар расширится до исходного давления (точка А).
На участке ВС не только давление, но и температура постоянны. Крайним точкам отрезка ВС соответствуют однофазные состояния вещества: точке С (объем 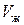 ) – жидкое, а точке В (объем
) – жидкое, а точке В (объем  ) – газообразное. В промежуточном двухфазном состоянии с объемом V часть вещества с количеством молей
) – газообразное. В промежуточном двухфазном состоянии с объемом V часть вещества с количеством молей 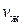 находится в жидком, а часть с количеством молей
находится в жидком, а часть с количеством молей  – в газообразном состоянии. Определим отношение количества молей жидкой и газообразной фаз в объеме
– в газообразном состоянии. Определим отношение количества молей жидкой и газообразной фаз в объеме  .
.
Объем одного моля жидкой и газообразной фаз вещества соответственно равны:
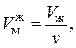
 . (3.1.1)
. (3.1.1)
Объем V содержит 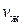 молей жидкой фазы и
молей жидкой фазы и  молей газообразной фазы, поэтому этот объем можно представить в виде суммы объемов жидкой и газообразной фаз следующим образом:
молей газообразной фазы, поэтому этот объем можно представить в виде суммы объемов жидкой и газообразной фаз следующим образом:
 . (3.1.2)
. (3.1.2)
После простых преобразований из выражения (3.1.2) находим искомое отношение
 . (3.1.3)
. (3.1.3)
Умножая числитель и знаменатель левой части выражения (3.1.3) на молярную массу  вещества, получим аналогичное отношение для масс жидкой и газообразной фаз:
вещества, получим аналогичное отношение для масс жидкой и газообразной фаз:
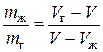 . (3.1.4)
. (3.1.4)
Таким образом, отношение масс жидкости и насыщенного пара в произвольном двухфазном состоянии определяемом объемом 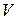 , равно отношению отрезков, на которое делит участок ВС точка, соответствующая объему
, равно отношению отрезков, на которое делит участок ВС точка, соответствующая объему 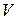 (рис. 47). Из формулы (3.1.4) легко видеть, что, чем ближе значение молярного объема
(рис. 47). Из формулы (3.1.4) легко видеть, что, чем ближе значение молярного объема 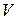 к
к 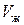 , тем большая часть вещества находится в жидком состоянии и тем меньшая – в газообразном. И, наоборот, чем ближе объем
, тем большая часть вещества находится в жидком состоянии и тем меньшая – в газообразном. И, наоборот, чем ближе объем 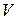 к
к  , тем большая часть вещества находится в газообразном состоянии, и тем меньшая его часть приходится на жидкость.
, тем большая часть вещества находится в газообразном состоянии, и тем меньшая его часть приходится на жидкость.
На рис. 47 представлены изотермы газа при различных температурах 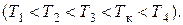 Из рисунка видно, что с ростом температуры горизонтальный участок, соответствующий двухфазному состоянию вещества, уменьшается и при некоторой температуре
Из рисунка видно, что с ростом температуры горизонтальный участок, соответствующий двухфазному состоянию вещества, уменьшается и при некоторой температуре  , называемой критической, стягивается в точку
, называемой критической, стягивается в точку 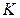 . Изотерма, соответствующая температуре
. Изотерма, соответствующая температуре  , называется критической изотермой, точка
, называется критической изотермой, точка 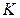 которой является точкой перегиба.
которой является точкой перегиба.
Из рис. 47 также видно, что с ростом температуры растет молярный объем 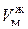 , занимаемый жидкостью, что равносильно уменьшению ее плотности
, занимаемый жидкостью, что равносильно уменьшению ее плотности  . И, наоборот, с ростом температуры уменьшается молярный объем
. И, наоборот, с ростом температуры уменьшается молярный объем  , занимаемый газом, что равнозначно увеличению его плотности
, занимаемый газом, что равнозначно увеличению его плотности 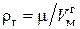 . В критическом состоянии
. В критическом состоянии 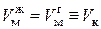 и
и 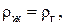 т. е. в состоянии, определяемом критическими параметрами
т. е. в состоянии, определяемом критическими параметрами 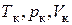 , исчезает всякое различие между жидкостью и ее насыщенным паром.
, исчезает всякое различие между жидкостью и ее насыщенным паром.
При температурах, больших критической, отсутствует область двухфазных состояний, вещество находится в газообразном состоянии. Это объясняется тем, что при температурах 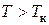 , кинетическая энергия поступательного движения молекул намного больше потенциальной энергии их взаимодействия и, естественно, вещество в таких условиях может находиться только в виде газа. Следовательно, даже сверхвысокими давлениями невозможно газ перевести в жидкое состояние, если его температура выше критической. Поэтому в XIX в. потерпели неудачу первые попытки сжижения некоторых газов, так как комнатная температура, при которой начиналось их сжатие, была значительно больше критической температуры. В качестве примера приведем экспериментальные значения критической температуры для некоторых веществ: для воды
, кинетическая энергия поступательного движения молекул намного больше потенциальной энергии их взаимодействия и, естественно, вещество в таких условиях может находиться только в виде газа. Следовательно, даже сверхвысокими давлениями невозможно газ перевести в жидкое состояние, если его температура выше критической. Поэтому в XIX в. потерпели неудачу первые попытки сжижения некоторых газов, так как комнатная температура, при которой начиналось их сжатие, была значительно больше критической температуры. В качестве примера приведем экспериментальные значения критической температуры для некоторых веществ: для воды 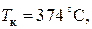 для углекислого газа
для углекислого газа  , для кислорода
, для кислорода 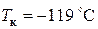 , для азота
, для азота  для водорода
для водорода  , для гелия
, для гелия  . Как видно из приведенных чисел, выбор Т. Эндрюсом углекислого газа для опытов был весьма удачен.
. Как видно из приведенных чисел, выбор Т. Эндрюсом углекислого газа для опытов был весьма удачен.
Если соединить между собой левые концы горизонтальных участков опытных изотерм, соответствующих двухфазному состоянию вещества, а затем то же самое проделать с правыми концами, то получится колокольного вида кривая АKВ, которая совместно с частью DK критической изотермы разделит плоскость 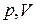 на три области (рис. 48).
на три области (рис. 48).
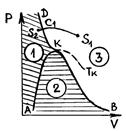
Р и с. 48
Пограничная кривая AK, называемая кривой кипения, отделяет однофазную область 1 жидкого состояния вещества от двухфазной области 2 насыщенного пара. Пограничная кривая конденсации BK отделяет двухфазную область 2 от однофазной области 3 газообразного состояния вещества. При давлениях, больших критического 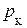 , отсутствует область двухфазного состояния. Вещество в этом случае может находиться или в газообразном или в жидком состоянии. Границей между ними служит часть DK критической изотермы.
, отсутствует область двухфазного состояния. Вещество в этом случае может находиться или в газообразном или в жидком состоянии. Границей между ними служит часть DK критической изотермы.
Наличие критической изотермы четко показывает, что между жидким и газообразным состояниями вещества нет принципиального качественного различия. В самом деле, из газообразного состояния  вещество можно перевести в жидкое состояние
вещество можно перевести в жидкое состояние 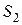 , по пути
, по пути 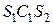 минуя область 2 двухфазного состояния (рис. 48). При этом нигде не будет происходить скачкообразное изменение состояния, вещество будет на всем пути перехода однородным.
минуя область 2 двухфазного состояния (рис. 48). При этом нигде не будет происходить скачкообразное изменение состояния, вещество будет на всем пути перехода однородным.
Дата добавления: 2015-04-18; просмотров: 369; Мы поможем в написании вашей работы!; Нарушение авторских прав |