
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Политропные процессы. Уравнение политропы идеального газа. Работа идеального газа при политропическом процессе.
Ранее рассматривались процессы, у которых имелись четко определенные постоянные признаки: изохорный процесс осуществлялся при постоянном объеме, изобарный – при постоянном давлении, изотермический – при постоянной температуре, адиабатный – при отсутствии теплообмена между веществом и внешней средой. Ясно, что наряду с этими процессами можно представить множество процессов, у которых имеются другие постоянные признаки.
Известно, что реальные процессы сжатия в газовых двигателях, компрессорах и т. д., как правило, не являются ни изотермическими, ни адиабатными, а занимают некоторое промежуточное положение в том смысле, что уравнение этих реальных процессов  имеет показатель степени отличный от
имеет показатель степени отличный от 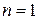 и от
и от 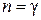 . Это так называемые политропные процессы.
. Это так называемые политропные процессы.
Всякий процесс, в котором теплоемкость является постоянной величиной, называют политропным.
Найдем уравнение политропы для идеального газа. Для этого в первый закон термодинамики

вместо элементарного количества тепла 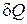 подставим
подставим 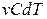 , вместо изменения внутренней энергии –
, вместо изменения внутренней энергии – 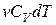 и вместо элементарной работы
и вместо элементарной работы  В результате получим:
В результате получим:
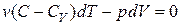 . (2.7.36)
. (2.7.36)
Из уравнения Менделеева – Клапейрона 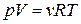 найдем
найдем 
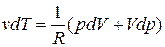 . (2.7.37)
. (2.7.37)
Подставим (2.7.37) в (2.7.36). В результате будем иметь:
 (2.7.38)
(2.7.38)
Учитывая, что для идеального газа 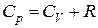 , получим:
, получим:
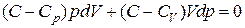 . (2.7.39)
. (2.7.39)
Разделим обе части последнего равенства на 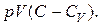 В результате оно примет вид:
В результате оно примет вид:
 (2.7.40)
(2.7.40)
Введя обозначение
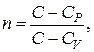 (2.7.41)
(2.7.41)
проинтегрируем обе части выражения (2.7.40). В результате интегрирования получаем:

Упрощая последнее соотношение, окончательно запишем:
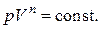 (2.7.42)
(2.7.42)
Это и есть искомое уравнение политропного процесса. Используя уравнение Менделеева – Клапейрона, легко получить уравнение политропы в других переменных:
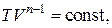 (2.7.43)
(2.7.43)
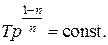 (2.7.44)
(2.7.44)
Из формулы (2.7.41) нетрудно найти выражение для теплоемкости  политропного процесса через показатель политропы
политропного процесса через показатель политропы 
 (2.7.45)
(2.7.45)
Уравнение (2.7.45) позволяет определить теплоемкость политропного процесса если известен показатель политропы 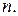 Последний определяется из экспериментальных данных. Пусть в начальном состоянии давление и объем газа были равны соответственно
Последний определяется из экспериментальных данных. Пусть в начальном состоянии давление и объем газа были равны соответственно 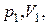 в конечном –
в конечном –  Тогда из уравнения политропы (2.7.42) находим
Тогда из уравнения политропы (2.7.42) находим 
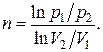 (2.7.46)
(2.7.46)
Подставив в (2.7.46) найденные из опыта величины, определим для данного реального процесса величину 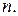
Покажем, что из уравнений политропного процесса как частный случай следуют четыре ранее рассмотренных процесса.
1. В изохорном процессе теплоемкость 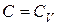 . Тогда знаменатель в (2.7.41) обращается в нуль, а числитель не равен нулю, так как
. Тогда знаменатель в (2.7.41) обращается в нуль, а числитель не равен нулю, так как  . Поэтому показатель политропы
. Поэтому показатель политропы 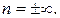 Причем
Причем  если теплоемкость
если теплоемкость  при стремлении к
при стремлении к  все время остается меньше
все время остается меньше  , в этом случае
, в этом случае 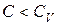 ,
,  и, как видно из (2.7.41),
и, как видно из (2.7.41), 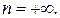 Величина
Величина 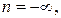 если теплоемкость
если теплоемкость  при стремлении к
при стремлении к  все время остается больше
все время остается больше  , тогда
, тогда 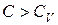 , но в пределе
, но в пределе  и, таким образом,
и, таким образом, 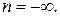 При этом из уравнения политропы (2.7.44) получим:
При этом из уравнения политропы (2.7.44) получим:
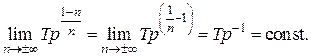
Откуда следует уравнение изохоры 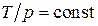 .
.
2. В изобарном процессе теплоемкость  и
и 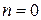 , т. к.
, т. к. 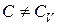 . Тогда из уравнения политропы (2.7.43) имеем:
. Тогда из уравнения политропы (2.7.43) имеем:
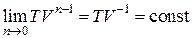 .
.
Отсюда следует уравнение изобары 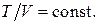
3. В изотермическом процессе теплоемкость  Тогда для показателя политропы получаем:
Тогда для показателя политропы получаем:
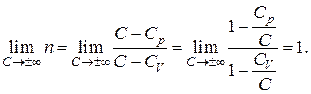
Подставляя это значение  в уравнение политропы (2.7.42), получим уравнение изотермы
в уравнение политропы (2.7.42), получим уравнение изотермы  .
.
4. Наконец, в адиабатном процессе 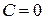 и
и 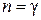 . В этом случае из уравнения политропы (2.7.42) следует уравнение адиабаты
. В этом случае из уравнения политропы (2.7.42) следует уравнение адиабаты  .
.
Используя результаты этих четырех случаев, а также формулу (2.7.45), можно построить график зависимости теплоемкости C политропного процесса от показателя политропы  .
.
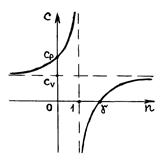
Р и с. 30
Из рис. 30 видно, что теплоемкость  , если показатель политропы принимает значение на интервалах
, если показатель политропы принимает значение на интервалах 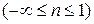 и
и 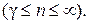 Этот результат следует из (2.7.45). В самом деле, если
Этот результат следует из (2.7.45). В самом деле, если 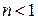 , то
, то  , т. к. всегда
, т. к. всегда 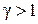 и, таким образом,
и, таким образом,  ; если же
; если же 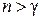 , то
, то  , т. к.
, т. к. 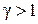 и снова
и снова 
 Из рис. 30 также видно, что политропный процесс, характеризуемый показателем
Из рис. 30 также видно, что политропный процесс, характеризуемый показателем 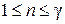 , имеет отрицательную теплоемкость. Это тоже следует из формулы (2.7.45). Действительно, в этом случае
, имеет отрицательную теплоемкость. Это тоже следует из формулы (2.7.45). Действительно, в этом случае  ,
, 
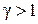 и теплоемкость
и теплоемкость 
Р и с. 31.
Интересно посмотреть расположение и характер уравнения политропы в переменных 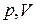 . На рис. 31 в качестве начального состояния газа взята точка А, через которую проведены кривые, соответствующие изохорному, изобарному, изотермическому и адиабатному процессам как в сторону расширения газа, так и в сторону его сжатия. Вся плоскость
. На рис. 31 в качестве начального состояния газа взята точка А, через которую проведены кривые, соответствующие изохорному, изобарному, изотермическому и адиабатному процессам как в сторону расширения газа, так и в сторону его сжатия. Вся плоскость 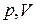 , таким образом, разбилась на восемь областей с определенными свойствами. Линии процессов, начинающиеся в точке А и расположенные в областях 1–4, соответствуют расширению газа и он, таким образом, производит работу против внешних сил
, таким образом, разбилась на восемь областей с определенными свойствами. Линии процессов, начинающиеся в точке А и расположенные в областях 1–4, соответствуют расширению газа и он, таким образом, производит работу против внешних сил 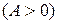 , а в областях 5–8 происходит сжатие газа и над ним совершается работа
, а в областях 5–8 происходит сжатие газа и над ним совершается работа 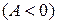 . Процессы, начинающиеся в точке A и лежащие в областях 4–7, совершаются с отводом теплоты, а в областях 1–3 и 8 – с подводом теплоты. Изотерма, вдоль которой внутренняя энергия идеального газа не изменяется
. Процессы, начинающиеся в точке A и лежащие в областях 4–7, совершаются с отводом теплоты, а в областях 1–3 и 8 – с подводом теплоты. Изотерма, вдоль которой внутренняя энергия идеального газа не изменяется 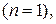 делит всю плоскость
делит всю плоскость 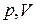 на две области, в одной из которых (области 1,2,7,8) внутренняя энергия газа возрастает (увеличивается температура), в другой (3–6) – убывает (уменьшается температура газа). Политропные процессы, протекающие в областях 3 и 6, имеют отрицательную теплоемкость. В пределах области 3 процессы происходят с подводом теплоты и с уменьшением температуры газа, а в области 6 совершаются с увеличением температуры газа и отводом теплоты.
на две области, в одной из которых (области 1,2,7,8) внутренняя энергия газа возрастает (увеличивается температура), в другой (3–6) – убывает (уменьшается температура газа). Политропные процессы, протекающие в областях 3 и 6, имеют отрицательную теплоемкость. В пределах области 3 процессы происходят с подводом теплоты и с уменьшением температуры газа, а в области 6 совершаются с увеличением температуры газа и отводом теплоты.
Если теплоемкость политропного процесса известна, то элементарное
количество теплоты полученное (отданное) идеальным газом в этом процессе, находится по формуле (2.5.4):
 (2.7.47)
(2.7.47)
Подставляя в последнее соотношение выражение теплоемкости из (2.7.45) и интегрируя его с учетом того, что для политропного процесса  , получим формулу для количества тепла:
, получим формулу для количества тепла:
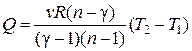 . (2.7.48)
. (2.7.48)
Отметим, что теплота, полученная идеальным газом при политропном процессе, в общем случае расходуется на изменение внутренней энергии и на совершение внешней работы.
Так как внутренняя энергия является функцией состояния, то ее изменение для любого процесса идеального газа
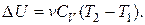 (2.7.49)
(2.7.49)
Составим соотношение из выражений (2.7.48–2.7.49)
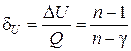 . (2.7.50)
. (2.7.50)
Коэффициент 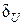 показывает, какая часть тепла, полученная при поли-тропном процессе, идет на увеличение внутренней энергии и опреде-ляется через показатели политропы и адиабаты. К примеру, для изохорного процесса
показывает, какая часть тепла, полученная при поли-тропном процессе, идет на увеличение внутренней энергии и опреде-ляется через показатели политропы и адиабаты. К примеру, для изохорного процесса 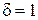 , т. е. все подведенное к газу тепло при изохорном процессе идет на увеличение его внутренней энергии.
, т. е. все подведенное к газу тепло при изохорном процессе идет на увеличение его внутренней энергии.
Аналогично вводится коэффициент
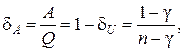 (2.7.51)
(2.7.51)
который показывает, какая часть тепла, полученная при политропном процессе, идет на совершение работы против внешних сил. Так, например, для изохорического процесса 
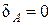 , т. е. внешняя работа в этом процессе не совершается. Легко видеть, что
, т. е. внешняя работа в этом процессе не совершается. Легко видеть, что 
Найдем работу, совершаемую в политропном процессе. Из уравнения политропы  определим давление
определим давление 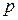 и подставим его в (2.4.5):
и подставим его в (2.4.5):
 (2.7.52)
(2.7.52)
Выполняя интегрирование, получим:
 (2.7.53)
(2.7.53)
где 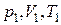 – соответственно давление, объем и температура газа в начальном состоянии,
– соответственно давление, объем и температура газа в начальном состоянии, 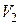 – объем в конечном состоянии.
– объем в конечном состоянии.
Из уравнения политропы  найдем
найдем 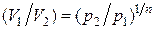 и подставим в (2.7.53). В результате будем иметь еще одно выражение для работы в политропном процессе:
и подставим в (2.7.53). В результате будем иметь еще одно выражение для работы в политропном процессе:
 (2.7.54)
(2.7.54)
Дата добавления: 2015-04-18; просмотров: 2305; Мы поможем в написании вашей работы!; Нарушение авторских прав |