Теплоемкость. Применение 1-го начала термодинамики для вычисления теплоемкости вещества.

Для вычисления количества теплоты, получаемой или отдаваемой системой при переходе из одного состояния в другое, используется понятие теплоемкости. Это одна из важнейших характеристик вещества. Различают молярную и удельную теплоемкости.

Молярной теплоемкостью называют количество тепла, которое необходимо сообщить одному молю, вещества, чтобы повысить его тем­пературу на 1К:

(2.5.1)

Удельной теплоемкостью называют количество тепла, которое нужно передать 1 кг вещества, чтобы повысить его температуру на 1К:

(2.5.2)

В последних формулах 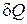– элементарное количество тепла, пере­данное веществу, – изменение его температуры, вызванное этим теплом, и – число молей и масса вещества соответственно.

Из формул (2.5.1–2.5.2) нетрудно получить связь между молярной и удельной теплоемкостями:

(2.5.3)

где – молярная масса.

Элементарное количество теплоты находится из выражения (2.5.1)

(2.5.4)

Количество теплоты, получаемое системой при нагревании от температуры 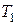до температуры ,

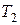(2.5.5)

Из опыта известно, что теплоемкость в общем случае зависит от температуры. Поэтому часто при вычислении количества тепла исполь­зуют понятие средней теплоемкости 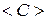. При этом количество теп­ла

(2.5.6)

где величину находят, используя теорему о среднем из матема­тического анализа:

(2.5.7)

Если же теплоемкость постоянна в интервале температур , то из выражения (2.5.5)

(2.5.8)

Теплоемкость, как собственное физическое свойство вещества, зависит от его природы (химического состава). При изо­термическом процессе система получает тепло а темпе­ратура все время сохраняется постоянной, т. е. , следователь­но, на основании выражения (2.5.1) имеем бесконечное значение теп­лоемкости для изотермического процесса . При адиаба­тическом процессе система не получает и не отдает тепла 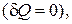хотя его температура изменяется , поэтому теплоемкость любых веществ при адиабатическом процессе равна нулю .

Зависимость теплоемкости от процесса объясняется тем, что коли­чество тепла 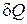, входящее в определение теплоемкости, не являет­ся функцией состояния, а зависит от пути перехода (процесса) системы из одного состояния в другое. Таким образом, у всякого вещества имеется бесконечное множество теплоемкостей, т. е. столько, сколько имеется путей перехода из одного состояния в другое. Чтобы устранить эту неоднозначность, сравнение теплоемкостей веществ производят при каком-нибудь заданном процессе. Обычно различают теплоемкости при постоянном объеме и теплоемкость при постоянном давлении , если в процессе нагревания поддерживаются постоянными соответственно объем вещества или давление. Причем для любых веществ . При их изохорическом нагревании работа системой не совершается. Поэтому все подводимое тепло, согласно первому закону термодинамики, идет на увеличение его внутренней энергии, т. е. на повышение его температуры. Если же давление системы при нагревании остается постоянным, то она должна расширяться (иначе давление будет расти), совершая внешнюю работу. В этом случае не все тепло, подводимое к системе, идет на изменение внутренней энергии, а часть этого тепла затрачивается на совершение работы. Следовательно, при постоянном давлении требуется большее количество теплоты для нагревания 1 моля вещества на 1К, чем при постоянном объеме.

, (2.5.12)

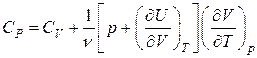^. (2.5.13)

Как видно из выражений (2.5.12–2.5.13), для нахождения и необходимо располагать явным видом двух функций: – внутренней энергии и – уравнением состояния вещест­ва. Для идеального газа эти функции нам известны (2.2.4; 1.9.3):

, (2.5.14)

. (2.5.15)

Подставив (2.5.14–2.5.15) в (2.5.12–2.5.13), получим

, (2.5.16)

. (2.5.17)

Для идеального газа теплоемкость при постоянном давлении больше теплоемкости при постоянном объеме на величину , которая численно равна работе при изобарическом нагревании 1 моля идеального газа на 1К. Для отношения теплоемкостей получим

. (2.5.18)

Из формул (2.5.16–2.5.17) видно, что теплоемкости и для идеального газа не зависят от температуры.

В сис­теме СИ ее размерностью, как видно из формулы (2.5.1), является

Теплоемкость молекулярного водорода (экспериментальная). Классическая теория теплоемкостей идеального газа. Ограниченность теоремы о равномерном распределении энергии по степеням свободы.

Теплоемкость идеальных газов от температуры не зависит и определяется только числом степеней свободы молекул. Как показывает опыт, это приблизительно так только для одноатомных газов; для других газов теплоемкость всегда растет с увеличением температуры.

На рис. 28 приведена экспериментальная зависимость молярной теплоемкости припостоянном объеме водорода от температуры.

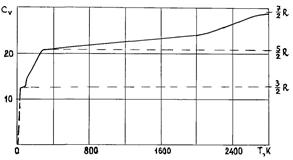
Р и с. 28

Как видно из графика, в области температур 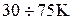теплоемкость постоянна и равна , т. е. она такая, как для одноатомного газа . Затем теплоемкость возрастает и в интервале температур 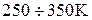снова приблизительно постоянна и равна , что соответствует, как мы знаем, теплоемкости газа, состоя­щего из жестких двухатомных молекул Далее при повышении температуры теплоемкость постепенно возрастает и при температуре в несколько тысяч градусов приближается к , что отвечает теплоемкости двухатомного газа, в котором возбуждены все возможные степени свободы 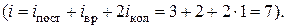Пунктирная часть кривой, стремящаяся к нулю, указывает ход теплоем­кости после перехода газообразного водорода сначала в жидкое, а затем в твердое состояние. Теплоемкость твердых тел стремится к нулю при приближении темпера­туры к абсолютному нулю.

Только квантовая теория позволяет объяснить эту зависимость теплоемкости водорода от температуры. Согласно положениям квантовой механики вращательная и колебательная энергии молекулы могут принимать не любые значения, а только дискретные: молекула может находиться лишь в некоторых так называемых стационар­ных состояниях, соответствующих определенным значениям энергии. Если молекула получает энергию в результате столкновений или излучения, то она может воспринимать эту энергию только определен­ными порциями (квантами).

При этом вращательная энергия молекулы в различных ста­ционарных состояниях

(2.6.1)

где h – постоянная Планка, I – момент инерции молекулы 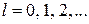– квантовое число, нумерующее квантовый уровень. Разность энергий между двумя ближайшими вращательными уровнями

(2.6.2)

и, таким образом, возрастает пропорционально .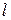

Колебательная энергия молекулы в стационарном состоянии

(2.6.3)

где 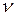– частота колебаний атомов водорода в молекуле, . Из (2.6.3) следует, что на нулевом колебательном уровне энергия колебаний молекулы равна . Это – нулевая энергия (чисто кванто-вый эффект), не исчезающая даже при абсолютном нуле температуры. Разность энергий между двумя ближайшими колебательными уровнями

(2.6.4)

и не зависит от п, т. е. уровни колебательной энергии распола­гаются на равных расстояниях друг от друга.

Энергетическое расстояние между двумя низшими уровнями для вращательной энергии из формулы (2.6.2)

(2.6.5)

а из формулы (2.6.4) для колебательной энергии

(2.6.6)

Рассчитаем по формулам (2.6.5–2.6.6) численные значения этих минимальных энергий квантов.

Известно, что расстояние между центрами атомов в молекуле водорода равно Поэтому радиус вращения молеку­лы Учитывая, что масса молекулы водорода , находим ее момент инерции , что по формуле (2.6.5) дает .

Из спектроскопических измерений известно, что частота колебаний молекулы водорода . Подставляя это значение в (2.6.6), получаем

Таким образом, минимальная энергия вращательного кванта примерно в 12 раз меньше 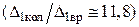, чем соответствую­щая энергия колебательного кванта.

Представим, что внутренняя энергия газообразного водорода распределена по трем сосудам, соответствующим энергиям поступа­тельного, вращательного и колебательного движений молекул. Пусть в исходном состоянии газ находится при низкой температуре, напри­мер, при При этом средняя кинетическая энергия поступа­тельного движения молекул, определяющая температуру газа, , что является величиной значительно меньшей . Это значит, что сосуд, содержащий энергию вращения молекул почти пуст: оннезначительно наполнен только молекулами с высокой энергией, которых очень мало, так как этим энергиям соответствует склон правой ветви колокольной кривой максвелловского распределе­ния по энергиям. Еще более пуст сосуд с энергиями колебаний молекул. Таким образом, при низкой температуре почти вся внутрен­няя энергия находится в сосуде, содержащем поступательную энергию молекул. Это значит, что молекулы газа движутся только поступательно и его теплоемкость равна . Этим состояниям газа соответствует примерно интервал температур 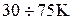(рис. 28).

Начнем увеличивать внутреннюю энергию газа, подводя к нему теплоту. Рост температуры приведет к тому, что сосуд, содержащий энергию поступательного движения молекул, начнет наполняться. Начнет наполняться и сосуд, в котором находится энергия вращения молекул, так как с ростом температуры максимум кривой распределения Максвелла смещается в сторону больших энергий, приводя к возраста­нию числа частиц с энергией достаточной для возбуждения первого уровня вращательного спектра. Процесс заполнения двух указанных сосудов обеспечит рост теплоемкости на интервале температур (рис. 28)

Когда все молекулы придут во вращательное движение возникнет, горизонтальный участок кривой, которому соответствует теплоемкость, равная . Температуры, соответствующие этому участку , еще недостаточны, чтобы в результате столкнове­ний за-метная часть молекул была способна возбудить первый колебательный уровень. Увеличение теплоемкости начнется при температуре около 350K, что свидетельствует о все большем вовлечении молекул водорода в процесс колебаний его атомов. При температуре примерно равной 4200K процесс роста теплоемкости прекратится, и она станет равной . В этом состоянии все вышеуказанные сосуды заполнены и энер-гия, содержащаяся в них, равна внутренней энергии газа. При этом каждая из молекул газа движется поступа­тельно, вращается, и атомы водорода в ней колеблются относительно центра инерции молекулы.

Так, в общих чертах, квантовая теория объясняет экспериментальные зависимости теплоемкостей при постоянном объеме от температуры для двухатомных газов, в частности, для молекулярного водорода.

Основные термодинамические процессы. Изохорный процесс. Изобарный процесс. Изотермический процесс. Уравнение изотермы идеального газа. Работа идеального газа при изотермическом изменении его объема.