Внутренняя энергия. Термодинамический метод. Выражение для внутренней энергии идеального газа.

Задачей термодинамики, как и молекулярно-кинетической теории (статистической физики), является установление зависимостей между физическими величинами, характеризующими рассматриваемое тело и окружающую среду, и непосредственно наблюдаемыми на опыте, т. е. мак­роскопическими величинами. Термодинамика, в отличие от статистической физики, не строит никаких модельных представлений об атомно-молекулярном строении вещества, поэтому в ней отсутствуют любые величины, характеризующие отдельные частицы (диаметры молекул и атомов, их масса, структура и т. п.).

Первый закон термодинамики непосредственно связан с зако­ном сохранения и превращения энергии.

Изначально первый закон термодинамики относился всего лишь к двум формам энергии: тепловой и механической, что позволяло с его помощью исследовать связи только между тепловыми и механически­ми явлениями.

Второй закон термодинамики – закон о возможности протекания любых самопроизвольных процессов.

Третий закон термодинамики – закон об абсолютном значении энтропии, фундаментальной величине в физике.

Термодинамический метод оказывается тем точнее, чем больше частиц в рассматриваемой системе, или чем меньше отно­сительные флуктуации рассматриваемых величин. Для систем, содержащих малое число частиц, термодинамика неприменима.

Внутренняя энергия есть сумма всех видов энергии движения и взаимодействия частиц, составляющих рассматриваемое тело, вычислен­ная в системе координат, в которой центр масс тела неподвижен. Поэтому внутренняя энергия не содержит кинетическую энергию движения тела как целого и ее потенциальную энергию во внешнем поле сил. Таким образом, внутренняя энергия складывается из кинетической энер­гии движения молекул, составляющих тело, кинетической энергии атомов внутри молекул, потенциальной энергии взаимодействия между молеку­лами, потенциальной энергии взаимодействия между атомами в молекуле, а также внутриатомной и внутриядерной энергии.

Наиболее просто получить выражение для вычисления внутренней энергии идеального газа. Так как молекулы идеального газа не взаимодейству­ют между собой, то его внутренняя энергия U равна

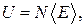(2.2.1)

где N – число молекул в газе, а средняя энергия , приходя­щаяся на одну молекулу, согласно теореме распределения, равна

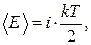(2.2.2)

где i – число степеней свободы молекулы определяемое по формуле (1.17.16).

Подставляя последнее выражение в (2.2.1), получим

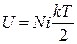. (2.2.3)

Умножив и разделив правую часть формулы (2.2.3) на число Авогадро 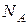, получим

. (2.2.4)

Учитывая, что 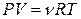, соотношение (2.2.4) можно представить в виде:

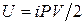. (2.2.5)

Как видно из формулы (2.2.4), внутренняя энергия идеального газа зависит от его температуры T, количества молей 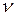и от сложности строения молекулы, характеризуемой ее числом степеней свободы i.

Внутренняя энергия должна являться функцией равновесного состояния системы, т. е. функция U должна однозначно определяться термодинамическими параметрами, характеризующими это состояние. Если бы это было не так, и в неко­тором состоянии система частиц могла обладать разными значениями внутренней энергии, т. е. последняя не была бы однозначной функцией состояния, то разность этих значений внутренней энергии можно было бы превратить в работу, не изменяя состояния тела, что противоречит закону сохранения энергии.

Выясним, каким математическим свойством должна обладать внутренняя энергия, если она действительно является функцией состояния системы.

Для этого переведем систему из состояния 1, характеризующегося объемом 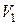и температурой 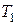, в состояние 2 с объемом 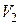и температурой 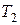. Обозначим внутреннюю энергию в состоянии 1 через 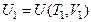, а в состоянии 2– 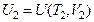. Так как внут­ренняя энергия – функция состояния, то ее изменение при этом перехо­де:

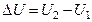. (2.2.6)

С другой стороны, это изменение внутренней энергии может быть най­дено суммированием бесконечно-малых изменений dU, т.е.

. (2.2.7)

Из выражений (2.2.6–2.2.7) заключаем, что

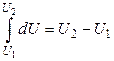. (2.2.8)

Последнее соотношение полностью совпадает с основной формулой, интегрального исчисления, выражающей обыкновенный определенный интеграл через первообразную. Откуда следует, что бесконечно-малая величина dU является точным (полным) дифференциалом:

. (2.2.9)

Если выражение (2.2.8) проинтегрировать по замкнутому контуру, то в результате получим нуль:

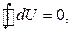(2.2.10)

так как при круговом процессе система возвращается к исходному состоянию и внутренняя энергия как функция состояния принимает свое начальное значение.

Нетрудно показать, что равенство (2.2.10) эквивалентно утверждению: изменение внутренней энергии при переходе системы из состояния 1 в состояние 2 не зависит от пути перехода, а определяется только координатами T,V начальной 1 и конечной 2 точек. В самом деле (рис. 23),

.

Из последнего равенства находим

(2.2.11)

т. е. разность 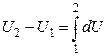действительно не зависит от пути перехода из 1 в 2.

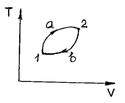
Рис. 23

Таким образом, следствием того, что внутренняя энергия являет­ся однозначной функцией состояния системы, служат соотношения (2.2.10–2.2.11), в которых подынтегральная функция – полный дифференциал.

В общем случае, чтобы установить, является ли произвольная функ­ция функцией состояния системы, используется следующая теорема из математического анализа: если значение криволинейного интеграла не зависит от пути интегрирования, а определяется только начальной и конечной точками интегрирования, то подынтегральное выражение представляет собой полный дифференциал некоторой функции, которую называют функцией состояния системы. Таким образом, функция состояния не за­висит от того процесса (пути), который к этому состоянию привел систему, а определяется только параметрами, характеризующими это состояние.

Следует обратить внимание, что внутренняя энергия как функция параметров состояния системы имеет смысл только для равновесных состояний, когда эти параметры имеют постоянные значения по всему объему системы. При неравновесных состояниях постоянные параметры, характеризующие эти состояния системы, не существуют.