Работа и количество тепла. Первый закон термодинамики. Работа при равновесном и неравновесном изменении объема системы.

Пусть внутренняя энергия системы изменилась за счет взаимодей­ствия с внешней средой на величину dU. По закону сохранения и превращения энергии таким же по абсолютной величине должно быть изменение энергии тех тел окружающей среды, с которыми провзаимодействовала система.

Полная работа, которой обменивается рассматриваемая система с окружающими телами,

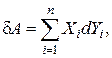(2.3.8)

где n – число разнородных воздействий (механических, электрических, магнитных и т. д.) на тело. Элементарную работу, совершаемую системой над внешними телами, условились считать положительной ; если работа совершается над системой, то ей приписывается отрица­тельный знак

Работа – это способ обмена энергией между системой и окружающей средой. Если такового обмена нет, то ни у рассматриваемой системы, ни у окружающей среды нет определен­ного количества работы, т. е. работа не является функцией состояния.

Способ изменения внутренней энергии системы не сопровожда­ется макроскопической (видимой) работой, т. е. при этом способе внешние тела не перемещаются или не изменяются действующие на систему внешние поля. Этот способ изменения внутренней энергии системы называют теплообменом (теплопередачей) и заключается он в том, что рассматриваемая система приводится в тепловой контакт с внешней средой, имеющей температуру, отличную от температуры самой системы.

Количество энергии, которым обменивается система и окружающая среда в процессе теплообмена, называют количеством теплоты.

Количество теплоты проявляется только в процессе обмена энер­гией системы и окружающей среды. У тела может быть только определенное количество внутренней энергии. Поэтому внут­ренняя энергия – функция состояния, а теплота, как и работа, не является функцией состояния.

Все три введенные величины –­­­­ внутренняя энергия, работа и теплота входят в уравнение первого закона термодинамики. Согласно этому закону, количество теплоты 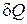, полученное системой, расходуется наизменение внутренней энергии и на совершение системой работы :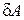

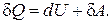(2.3.9)

Если система частиц изолирована, т. е. не обменивается энергией с окружающей средой ни в форме работы 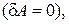ни в форме теплоты 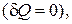то 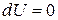и внутренняя энергия сохраняется (U = const). Таким образом, первый закон термодинамики – это при­ложение более общего закона сохранения энергии к термодинамическимпроцессам, при которых происходит превращение работы, пони­маемой в обобщенном смысле (2.3.8), в теплоту и теплоты в работу.

Пусть газ, заключенный в цилиндр и закрытый сверху невесомым подвижным поршнем, находится в равновесии. Это значит, что давление газа p равно внешнему давлению 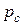среды (рис. 24).

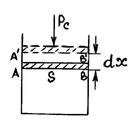
Р и с.24

Поло­жим, что газ бесконечно медленно (равновесно) расширился за счет полученного тепла и поршень переместился на 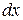из положения АВ в положение 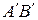. Вычислим работу, которую при этом совершил газ. Работа эта заключается в том, что газ при расширении преодолевает внешнее давление 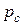, под которым он находится. По определению работы

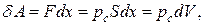(2.4.1)

где 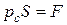– внешняя сила давления, преодолеваемая газом, а 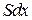– увеличение объема газа при его расширении, 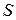– пло­щадь поршня.

Работа расширения, совершаемая газом, при конечном изменении объема

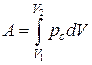(2.4.2)

Ясно, что работа расширения против сил внешнего давления произво­дится только тогда, когда изменяется объем тела 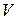и когда внеш­нее давление 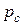не равно нулю. Если же 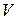сохраняется постоян­ным, то какие бы изменения ни претерпевали любые другие параметры, характеризующие состояние газа (температура, давление, внутренняя. энергия и т. д.), работа расширения всегда будет равна нулю. С другой стороны, если объем газа изменяется, но внешнее давление все время равно нулю 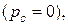как это имеет место при расшире­нии газа в вакуум, то работа расширения тоже равна нулю. Поэтому с точки зрения возможности совершения газом работы против внешнего давления 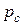параметр 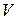является жестко связанным с этим давлением, как говорят, сопряжен с ним.

Знак работы определяется знаком 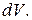Так как абсолютное давление – существенно положительная величина, то при расширении 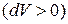работа производится газом над внешней средой и, как видно из соотношений (3.4.1–3.4.2), положительна, при сжатии работа совершается внешней средой над газом и, как видно из тех же соотношений, отрицательна.

Формулы (2.4.1–2.4.2) справедливы не только для газов, но и для жидких и твердых тел. Рассмотрим, например, твердое тело, помещенное в жидкую или газообразную среду, которая при от­сутствии внешних полей оказывает одинаковое давление на любые участки поверхности этого тела (рис. 25)

Р и с. 25

Постоянство давления 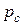легко объясняется тем, что молекулы среды, находящейся в сос­тоянии равновесия, движутся по всем направлениям с одинаковой ве­роятностью, с одинаковыми средними скоростями и на каждую единицу поверхности тела приходится в среднем одинаковое число ударов молекул одинаковой силы (закон Паскаля). При наличии внешнего поля силы тяжести давление 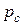также можно считать постоянным на всей поверхности тела, если размеры его таковы, что можно пренебречь изменениями гидростатического давления.

Пусть при расширении тела элементарные участки его поверхности 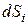переместились по нормали к ним на расстояние 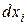. Тогда работа на i-м участке

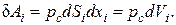
Полная работа тела по увеличению объема на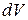

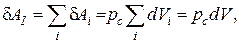
что совпадает с формулой (2.4.1).

Чтобы процесс был равновесным, он должен протекать бесконечно медленно. При этом давление газа 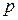и внеш­нее давление среды 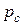отличаются на бесконечно малую величину, т. е. для равновесных процессов справедливо равенство

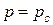(2.4.3)

Поэтому формулы (2.4.1–2.4.2) для равновесного процесса приобретают вид:

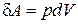, (2.4.4)

(2.4.5)

где 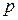– давление газа (внутреннее давление в системе), которое может быть вычислено из уравнения состояния, например, из уравне­ния Менделеева – Клапейрона, если газ идеальный. Особо отметим, что формулы (2.4.4–2.4.5) справедливы только для равновесных процессов. Если процесс неравновесный, то давление газа отличается от давле­ния окружающей среды на конечную величину. В этом случае расширение газа протекает с конечной скоростью, внешнее давление 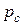меньше давления 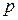газа на конечную величину и, соответственно, полезная работа при неравновес­ном процессе меньше полезной работы 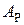при равновесном процессе, т. е.

. (2.4.6)

При неравновесном сжатии, наоборот, внешнее давление больше давле­ния газа, поэтому и затраченная работа на сжатие больше, чем в слу­чае равновесного процесса, т. е.

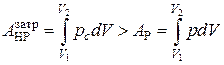(2.4.7)

При неравновесных процессах работа расширениявсегда меньше а работа сжатия больше, чем при равновесных процессах.