Флуктуация. Зависимость относительной флуктуации от числа частиц в системе. Роль флуктуации в науке и технике.

Флуктуацией называют случайное отклонение физических величин от их средних значений. За количественную меру флуктуации принима­ют среднеквадратическое значение случайной величины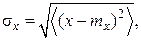

Флуктуации макроскопических величин вызываются беспорядочным тепловым движением молекул, образующих рассматриваемую систему.

Даже в состоянии равновесия наблюдаемые физические величины испытывают флуктуации около своих средних значений. Это легко заметить на опыте при измерении, например, величины давления рав­новесного состояния газа двумя разными манометрами: быстродейству­ющим (чувствительным) и инерционным (грубым) (рис. 19).

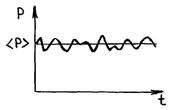
Р и с. 19

Из рис. 19 видно, что инерционный манометр показывает постоянное, равное среднему, давление, тогда как быстродействующий, успевая реа­гировать на малые изменения действующей на него силы, обнаруживает колебания около среднего значения.

Если система состоит из N невзаимодействующих молекул, то относительная флуктуация любой аддитивной физической величины Ф, значение кото­рой для всей системы в целом равно сумме ее значений φ_i для всех молекул, убывает обратно пропорционально корню квадратному из чис­ла молекул в системе. Докажем это утверждение.

Рассмотрим аддитивную величину Ф, например, суммарную кинетическую энергию хаотического теплового движения N молекул. Тогда

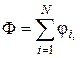
где 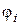– кинетическая энергия i-й молекулы. Среднее значение

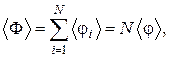(1.16.1)

так как в состоянии равновесия для одинаковых молекул их средние равны, т. е.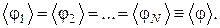

При вычислении дисперсии величины Фучтем, что дисперсия суммы независимых (невзаимодействующих) величин равна сумме их дисперсий, т. е.

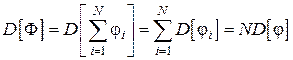. (1.16.2)

Извлекая корень квадратный из обеих частей (1.16.2), получим соотношение для среднеквадратических величин, т. е.

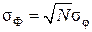. (1.16.3)

Таким образом, абсолютная флуктуация аддитивной величины Ф растет пропорционально 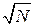. Однако важна не абсолютная флуктуация величины Ф, существенным является во сколько раз она меньше среднего значения Ф, возле которого происходят эти флуктуации, т. е. имеет значение относительная флуктуация:

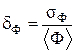. (1.16.4)

Подставляя (1.16.1) и (1.16.3) в (1.16.4), получим

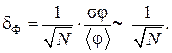(1.16.5)

Из соотношения (1.16.5) следует, что относительные флуктуации всех физических величин, значения которых для всей системы равно сумме значений их для всех молекул, обратно пропорционально корню из числа частиц в системе. Так как число молекул в макроскопической системе обычно порядка числа Авогадр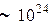о ( ), то 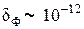, что является ничтожно малой величиной. Это означает, что величина флуктуации 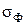меньше среднего значения 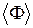примерно в 1012 раз. Если обратиться к рис. 19, то такие флуктуации давления невозможно изобразить ни в каком линейном масштабе: они просто сольются с прямой, соответствующей 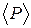. Поэтому можно утверждать, что средние значения макроскопических величин Ф при большом числе молекул в рассматриваемой системе совпадают с их истинными (измеримыми на опыте) значениями. Однако, если число молекул в рассматриваемой системе невелико, то истинное значение Ф будет существенно отличаться от среднего значения Ф.