Распределение Максвелла-Больцмана

Из соотношений (1.10.5), (1.10.6) и (1.10.34) следует, что число молекул, обладающих почти заданным направлением движения, определяем вектором ,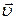

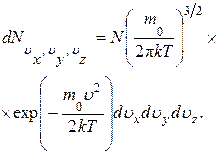(1.14.1)

Разделим обе части (1.14.1) на объем V, занимаемый газом. В результате получим

(1.14.2)

где 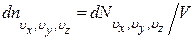– число молекул в единице объема газа, компоненты скоростей которых заключены в интервалах (υ_x, υ_x + dυ_x), (υ_y, υ_y + dυ_y), (υ_z, υ_z + dυ_z), 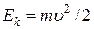– кинетическая энергия молекулы, n – число любых молекул в единице объема. Если внешнее поле отсутствует, то концентрация n постоянна по всему объему газа. Если же на газ наложено внешнее поле, то концентрация n молекул определяется формулой Больцмана. Подставив (1.13.18) в (1.14.2), получим

(1.14.3)

где E = E_k +E_P - полная энергия молекулы.

Выражение (1.14.3) определяет число молекул в единице объема, взятого около точки с координатами x,y,z, компоненты скорости которых имеют направления движения близкие к направлению, определяемому вектором 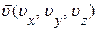. Формула (1.14.3) объединяет в себе закон Максвелла (1.10.34) о распределении молекул по скоростям и закон Больцмана (1.13.18) о распределении молекул по пространству во внешнем поле, и поэтому называется законом Максвелла – Больцмана.

Число молекул в объеме dV, находящемся около точки с коорди­натами x,y,z, имеющих проекции скоростей в интервалах (υ_x, υ_x + dυ_x), (υ_y, υ_y+dυ_y), (υ_z, υ_z+dυ_z), равно

(1.14.4)

а вероятность, что какая-либо молекула находится в объеме dV с указанными выше проекциями скоростей, равна

, (1.14.5)

где 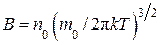, а постоянная С находится из условия нормировки:

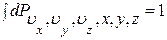. (1.14.6)

В распределении Максвелла – Больцмана полная энергия Е молекулы может принимать любые значения. В квантовой теории энергия молекулы может принимать лишь дискретные значения Е₁,Е₂,… В этом случае формула (1.14.4) заменяется следующей

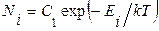, (1.14.7)

где N_i – число молекул в газе, которые обладают энергией E_i Формула (1.14.5) для квантового случая приобретает вид

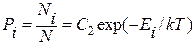, (1.14.8)

где постоянная C₂ находится из равенства

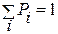, (1.14.9)

т. е. .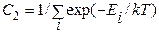

Таким образом, распределение Максвелла – Больцмана (1.14.8) для квантового случая запишется так

. (1.14.10)

Распределение Максвелла –Больцмана разбивается на произведение двух сомножителей (исключая постоянные множители):

,

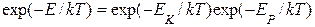один из которых относится к распределению Максвелла по скоростям, другой – к распределению Больцмана по пространственным координатам молекул. Из теории вероятностей известно, что если совместная плотность вероятности двух случайных величин равна произведению плотностей вероятностей этих величин, то эти величины независимы. Таким образом, можно утверждать, что распределение Максвелла устанавливается при постоянной температуре независимо от того есть внешнее поле или его нет. И наоборот, распределение Больцмана также устанавли­вается всегда при постоянной температуре и не зависит от распределения скоростей молекул. Отсюда следует важный вывод: наложение на газ внешнего поля не может изменить среднюю квадратичную скорость молекул (температуру газа), так как она полностью определяется не зависящим от этого поля распределением Максвелла по скоростям.