Температура и ее измерение. Эмпирические (Опытные) температурные шкалы. Идеально-газовая шкала температур.

Если привести в соприкосновение два тела с различной степенью нагретости, то молекулы этих тел, сталкиваясь между собой, будут передавать друг другу энергию. При этом тело, которое теряет энергию, называют более нагретым, а тело, которому переходит энергия – менее нагретым. Известно, что макроскопический (суммарный) переход энергии продолжается до тех пор, пока не установится макроскопическое тепловое равновесие между этими телами. В таком состоянии макроскопического перехода энергии от одного тела к другому не будет, хотя на микроскопическом уровне молекулы будут обмениваться энергией.

Для характеристики степени нагретости тел служит понятие температуры. Для сравнения температуры различных тел достаточно выбрать одно из этих тел, которое называется термометрическим телом.

Выбор термометрического тела не является произвольным. Его выбирают таким, чтобы физическая величина, характеризующая состояние этого тела, зависела от температуры. При этом она должна быть: 1) непрерывной; 2) монотонной, т. е. не иметь разных значений при одной и той же температуре; 3) точно измеряемой простым и удобным способом; 4) точно воспроизводимой; 5) иметь как можно большее приращение при изменении температуры на один градус (высокая чувствительность); 6) независимой от влияния других факторов, кроме температуры. Величина, удовлетворяющая перечисленным условиям, называется термометрической величиной.

Вообще говоря, нет ни одной физической величины, которая в полной мере удовлетворяла перечисленным требованиям во всем интервале измеряемых температур. В большей или меньшей степени этим условиям удовлетворяют следующие физические величины зависящие от температуры: давление идеальных газов при постоянном объеме, объем некоторых жидкостей при постоянном давлении, сопротивление металлов, проводимость полупроводников, термоэлектродвижущая сила контактных соединений металлов, интенсивность электромагнитного излучения тел.

Функцию t = f(x), выражающую закономерное соотношение между температурой и показанием термометра, называют уравнением термометра.

Вид функциональной зависимости между температурой и термометрической величиной первоначально можно выбрать только произвольно. Простоты ради ее выбирают линейной, т. е. полагают

(1.6.1)

где а и b – постоянные. Постоянная а определяется выбором единицы измерения температуры.

Выбрав термометрическое тело и термометрическую величину, а также определив уравнение термометра , установим единицу измерения температуры – градус.

Положим в уравнении (1.6.1) t = t₁ и t = t₂. В результате будем иметь

(1.6.2)

где х₁, х₂– измеренные в опыте значения термометрической величины в реперных точках t₁ и t₂.

(1.6.6)

Запишем уравнение (1.6.6) для шкал Цельсия, Реомюра и Фаренгейта:

(1.6.8)

(1.6.9)

(1.6.10)

Для измерения температуры необходима такая термометрическая величина, изменение которой при изменении температуры было бы независимо (или слабо зависимо) от химической природы вещества.

Такой термометрической величиной описывается газообразное состояние вещества, подчиняющееся уравнению Клапейрона – Менделеева:

(1.7.1)

В абсолютной идеально-газовой шкале так же, как и в шкале Цельсия, разность температур между двумя реперными точками (температурой Т₁ плавления льда и температурой Т₂ кипения воды при нормальном атмосферном давлении) принимается равной 100, т. е. один градус в шкале Цельсия равен одному градусу в абсолютной шкале по определению. Таким образом, в абсолютной шкале

Т₂ – Т₁=100. (1.7.3)

Второе уравнение для определения значений температур в реперных точках абсолютной шкалы находится измерением давлений P₁ и P₂ соответствующих температурам Т₁ и Т₂ в реперных точках. Эти измерения дают

(1.7.4)

Решая уравнения (1.7.3)–(1.7.4), находим

Т₁=273,15 К, Т₂=373,15 К.

(1.7.8)

где P₁ – давление в газовом термометре, находящемся в тающем льду. Чтобы при помощи газового термометра измерить температуру тела, необходимо это тело привести в тепловой контакт с газовым термометром и измерить манометром давление газа в нем. Тогда температура Т вычисляется по формуле (1.7.8).

Ввиду того, что так называемая тройная точка воды (одновременное сосуществование в равновесии трех фаз воды твердой, жидкой и газообразной) значительно лучше воспроизводится на опыте, чем точки плавления льда и кипения воды, в 1954 г. по международному соглашению абсолютная шкала или шкала Кельвина строится по одной реперной точке – тройной точке воды температуре которой приписываются точно Т_тр= 273,16 К (или 0,01 °С).

Тогда любая температура Т, измеряемая газовым термометром определяется по формуле, аналогичной (1.7.8):

(1.7.9)

И, наконец, для шкал Кельвина и Цельсия на основании выражений (1.6.6) и (1.6.8)

(1.7.10)

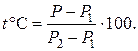(1.7.11)

Вычитая из (1.7.10) выражение (1.7.11), получим связь между шкалами Кельвина и Цельсия:

Т,К= t °С+273,15. (1.7.12)

21. Температура – мера средней кинетической энергии поступательного движения молекул. Молекулярно-кинетический смысл температуры.

Уравнение кинетической теории газов для давления:

(1.8.1)

При постоянном объеме V = const газа и постоянном в нем числе молекул N = const (тогда и концентрация молекул n = N/V = const) из этого уравнения следует, что давление идеального газа пропорционально средней кинетической энергии поступательного движения его молекул:

Р ~ , (V = const, N =const) (1.8.2)

Температура газа пропорциональна средней кинетической энергии поступательного движения молекул

(1.8.4)

По определению полагают температуру θ, выраженную в энергетических единицах (джоулях), равной 2 /3, т. е.

(1.8.5)

Если температуру измерять в градусах, то необходимо ввести коэффициент, переводящий единицы энергии (джоули) в градусы (Кельвины), т. е.

θ=kT (1.8.6)

Коэффициент k называют постоянной Больцмана, появление которой в физике весьма условно. Ее численное значение находится из опыта и по современным данным Дж/К.

Из (1.8.5) и (1.8.6) следует, что

(1.8.7)

Таким образом, измеряя температуру, мы измеряем фактически кинетическую энергию поступательного хаотического движения одной молекулы.

Абсолютная температура равновесного состояния не может быть отрицательной, т.е. Т ≥ 0.

22. Уравнение Менделеева – Клапейрона (Уравнение состояния идеального газа). Законы идеального газа (следствия из этого уравнения).

Р = nkТ. (1.9.1)

Учитывая, что n = N/V и N/N_А = m/μ = ν, получим

, (1.9.2)

где введена постоянная R=kN_A=8,31Дж/мольּК, которую называют универсальной газовой постоянной. Физический смысл ее установим из уравнения (1.9.2):

, (1.9.3)

которое называют уравнением Менделеева – Клапейрона. Для этого запишем уравнение (1.9.3) для двух состояний изобарического процесса:

PV₁= νRT_1,

РV₂=νRТ_2.

(1.9.4)

Обозначая V₂ – V₁=ΔV, T₂ – T₁=ΔT и учитывая, что работа при изобарическом процессе

А = РΔV, из (1.9.4) найдем R.

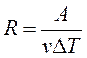, (1.9.5)

т. е. постоянная R численно равна работе при изобарическом нагревании на один Кельвин (ΔТ = 1К) одного моля (ν = 1моль) идеального газа. Так как k = R/N_A, то постоянная Больцмана имеет тот же смысл, что и R, только рассчитанная на одну молекулу.

Из уравнения состояния идеального газа (1.9.3) можно получить известные из опыта газовые законы.

1. Полагая в уравнении (1.9.3) ν = const и Т = const, получаем

PV = const. (1.9.6)

Формулировка закона Бойля – Мариотта (изотермический процесс): при неизменных массе и температуре идеального газа произведение его объема на давление есть величина постоянная.

2. При изобарическом процессе P = const.Также ν = сonst. Поэтому из уравнения состояния (1.9.3) в этом случае

, (1.9.7)

т. е. при неизменных массе и давлении идеального газа отношение объема, занимаемого газом, к его температуре – величина постоянная. Это утверждение известно как закон Гей-Люссака.

3. Пусть процесс протекает при постоянном объеме V=const (по

прежнему ν = сonst). Тогда из (1.9.3)

(1.9.8)

т. е. при неизменных массе и объеме идеального газа отношение давления газа к его температуре есть величина постоянная. Уравнение (1.9.8), называемое уравнением изохорического процесса, выражает известный закон Шарля.

4. Из уравнения (1.9.3), очевидно, также следует объединенный закон

Мариотта – Гей- Люссака

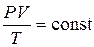, (1.9.9)

т. е. произведение давления газа на его объем, деленные на абсолютную температуру, для данной массы газа есть величина постоянная.

5. Из уравнения (1.9.3) также следует закон Авогадро, согласно которому при одинаковых давлениях и температурах в равных объемах любого газа содержится одинаковое число молекул. Действительно, пусть имеются два одинаковых объема двух различных газов при одинаковых давлениях и температурах. Для каждого из них можно написать уравнение состояния (1.9.2)

PV = N₁kT, PV = N₂kT,

где N₁ и N₂ – число молекул обоих газов. Из этих равенств непосредственно следует, что N₁= N₂. Это и есть закон Авогадро. Из него, очевидно, следует и обратная формулировка: различные газы, но содержащие одинаковое число молекул, будут при одинаковых давлениях и температурах занимать одинаковые объемы. Поэтому моль любого газа при данных давлении и температуре занимает одинаковый объем. В частности, при нормальных условиях (Т₀= 273,15К, Р_атм= 1,01ּ10⁵ -Па) моль любого газа занимает объем

.

6. Следствием уравнения идеального газа является и закон Дальтона, утверждающий: давление смеси химически не реагирующих газов равно сумме парциальных давлений отдельных газов. Парциальным давлением называют давление, которое создал бы газ, если бы он находился один в объеме, занятом смесью.

7. Следствием уравнения Менделеева – Клайперона является закон Амага: объем смеси химически нереагирующих идеальных газов равен сумме их парциальных объемов, т. е.

(1.9.13)

где парциальный объем

(1.9.14)

Как видно из выражения (1.9.14), парциальный объем V_i есть объем, который занимал бы i-й газ, если бы все остальные газы были удалены, а давление Р и температура Т остались неизменными.

Распределение Максвелла (Распределение молекул газа по скоростям). Постановка задачи о распределении молекул по компонентам скорости и по абсолютной величине скорости. Границы применимости распределения Максвелла.

В газе, находящемся в равновесии при температуре T, скорость любой молекулы из-за столкновений непрерывно меняется как по абсолют­ной величине, так и по направлению. Распределение по направлениям движения в состоянии равновесия равновероятно. Если бы это было не так, то в каком-то направлении в газе двигалось бы боль­шее число молекул, чем в другом. В результате возник бы макроскопи­ческий поток газа и газ не находился бы в равновесии.

Иначе обстоит дело с абсолютными значениями скоростей молекул: они не будут равновероятны, т. е. функция плотности вероятности F(υ) принимает неодинаковые значения при различных скоростях молекул. При этом, наибольшее число молекул будет группироваться около некоторой средней скорости, к примеру, около средней квадратичной υ_кв,

Распределение молекул по скоростям должно иметь максимум около среднего квадратичного значения скорости и убывать до нуля от этого максимального значения в сторону больших скоростей молекул. Найдем, следуя Максвеллу, явный вид этой функции.

Спроектируем скорости всех N молекул газа на ось x. Вероятность того, что произвольно взятая молекула име­ет проекцию скорости, заключенную в интервале (υ_x , υ_x+ dυ_x), будет равна

, (1.10.2)

где – число молекул в газе, которые имеют проекцию скорости, заключенную в интервале (υ_x, υ_x+dυ_x). С другой стороны эта вероятность может быть выражена через плотность вероятности φ(υ_x)

(1.10.3)

Сравнивая выражения (1.10.2) и (1.10.3) , находим

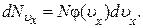(1.10.4)

Аналогичные соотношения могут быть записаны для проекций скоростей молекул на оси Y и Z.

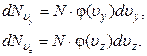
Вероятность того, что случайно взятая молекула имеет проекции скорости, заключенные в интервалах (υ_x, υ_x + dυ_x), (υ_y, υ_y + dυ_y) и (υ_z, υ_z + dυ_z) или, то же самое, что эта молекула движется в направлении, близком к направлению, определяемом вектором . Пo определению вероятности, она равна

(1.10.5)

где – число молекул, компоненты скорости которых лежат в указанных выше интервалах. Если обозначить совместную плотность вероятности проекций скорости молекул через 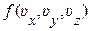, то та же вероятность (1.10.5), может быть представлена в виде

(1.10.6)

Из выражений (1.10.5) и (1.10.6) следует, что

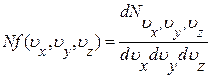(1.10.7)

Функция для равновесного состояния не зависит от времени. Также эта функция не может зависеть от направления вектора скорости молекул, определяемого проекциями υ_x,υ_y,υ_z, т. к. в состоянии равновесия все направления равновероятны. Она может за­висеть только от длины вектора скорости, т. е. ,

где .

Наряду с введенными функциями φ и f, рассмотрим распределе­ние молекул F(υ) по абсолютной величине скорости. Распределение F(υ)определяется вероятностью того, что величина скорости молекулы заключена в пределах от υ до υ + dυ независимо от направления, т. е.

, (1.10.8)

где – число молекул, величина скорости которых находится в интервале (υ , υ + dυ).

Функции F(υ) и f(υ) жестко связаны друг с другом:

(1.10.10)

Далее Максвелл предположил, что события, заключающиеся в попадании проекций υ_x, υ_y, υ_z скорости данной молекулы в интервалы

(υ_x, υ_x + dυ_x), (υ_y, υ_y + dυ_y) и (υ_z, υ_z + dυ_z)соответственно, явля­ются независимыми событиями. Тогда, согласно теореме умножения, совместная вероятность этих событий равна произведению их вероятностей, т. е.

(1.10.11)

На основании формул (1.10.6) и (1.10.3), равенство (1.10.11) можем переписать в виде:

(1.10.12)

Разделив обе части (1.10.12) на и учитывая, что , получим

. (1.10.13)

Прологарифмируем последнее равенство

. (1.10.14)

Дифференцируя выражение (1.10.14) на компоненте скорости υ_x , получим

. (1.10.15)

Учитывая, что , производная

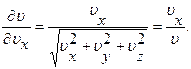(1.10.16)

Это позволяет записать соотношение (1.10.15) в виде

(1.10.17)

Аналогичные выражения могут быть получены при дифференцировании (1.10.14) по двум другим компонентам скорости υ_y и υ_z:

(1.10.18)

(1.10.19)

Правые части этих равенств равны друг другу, так как левые части их одинаковы. Правая часть (1.10.17) не зависит от υ_y и υ_z. Значит, от них не зависит и левая часть. Аналогично, правая часть (1.10.18) не зависит от υ_x и υ_z, откуда следует независимость и левой части от этих величин. Но тогда и правая часть (1.10.17) не зависит от υ_х. Это возможно только в том случае, если

(1.10.20)

Умножим обе части (1.10.20) на υ_хdυ_х. В результате будем иметь

(1.10.22)

Интегрируя, получаем

. (1.10.23)

Откуда находим

(1.10.24)

Из-за равной вероятности направлений движения молекул точно такой же вид имеют функции и . Для нахождения двух постоян­ных С и С₂, необходимо располагать двумя уравнениями для искомой функции φ. Первое уравнение – это условие нормировки плотности вероятности :

. (1.10.25)

Второе уравнение – это связь средней кинетической энергии поступательного движения молекулы с температурой:

(1.10.26)

Очень большие скорости моле­кул должны быть маловероятными. Это возможно только в том случае, если постоянная в формуле (1.10.24) отрицательна, т. е.

С = – С₁ (С₁>0) .

Поэтому (1.10.24) примет вид

. (1.10.27)

В выражении (1.10.25) максимально возможная проекция на ось Х скорости молекул, находящихся при температуре T, положена равной бесконечности, что физически нереально. Однако увеличение интервала интегрирования сверх некоторой максимальной скорости не приведет к заметной ошибке ввиду того, что функция (1.10.27) быстро убывающая.

Подставляя (1.10.27) в (1.10.25) и интегрируя, получим

(1.10.28)

Откуда находим 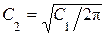и, следовательно,

(1.10.29)

Чтобы воспользоваться равенством (1.10.26) для нахождения постоянной С₁учтем, что

, (1.10.30)

так как ввиду равновероятности направлений движения молекул = = . Поэтому достаточно вычислить средний квадрат одной из компонент скорости:

. (1.10.31)

Используя формулы (1.10.31), (1.10.30) и (1.10.26), находим

(1.10.32)

Подстановка постоянной (1.10.32) в (1.10.29) дает

(1.10.33)

Точно такие же формулы будут справедливы и для других проекций скорости молекул. Поэтому функция (1.10.13)

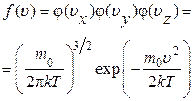, (1.10.34)

а функция распределения по абсолютным значениям скорости (1.10.10)

. (1.10.35)

Максвеллом было сделано предположение: проекции скорости молекул статистически независимы. Это предположение им не было доказано или обосновано. В дальнейшем американским физиком-теоретиком Д. Гиббсом было доказано, что условие независимости компонент скорости имеет место тогда, когда кинетическая энергия квадратична по компонентам импульсов; последнее справедливо всегда, за исключением случая релятивистских скоростей частиц.

Как доказывается в статистической физике, классический способ изложения применим, если температура Т равновесного состояния системы частиц значительно больше так называе­мой температуры вырождения

T_B , т. е.

, (1.10.36)

где h и k – постоянные Планка и Больцмана, m₀ – масса частицы, n – концентрация частиц.

Систему частиц, находящуюся при температуре T < T_B , называют вырожденной. К этой системе частиц применимо только квантовое рас­смотрение, которое приводит к распределению по скоростям (энергиям), существенно отличающемуся от максвелловского.

Свойства распределения Максвелла. Наиболее вероятная скорость молекул. Средняя арифметическая и средняя квадратичная скорости газовых молекул и их вычисление на основе закона Максвелла. Среднее значение квадрата компоненты скорости молекул газа.

В состоянии равновесия при отсутствии внешних полей распределение молекул газа по простран­ству в сосуде будет однородным, т. е. в любом физически бесконеч­но малом объеме содержится одинаковое число молекул. Рассмотрим теперь тот же газ не в обычном пространстве x, y, z, а в про­странстве скоростей . Если газ состоит из N моле­кул, то в любой момент времени в пространстве скоростей будет зафиксировано N точек, отвечающих N векторам скоростей моле­кул. На рис. 11, а и 12, а представлены N точками концы проекций век­торов скоростей молекул газа на плоскость (проекция трехмерной картинки на плоскость).

Как видно из формулы Максвелла (1.10.34) и из рис. 11, а (или рис. 12, а) в разных частях пространства скоростей, соответствующих различных скоростям, будет находиться неодинаковое число молекул, т. е. плотность числа частиц в пространстве скоростей будет убывать с уве­личением скорости, т. е. с увеличением расстояния от начала коор­динат, соответствующего нулевой скорости. Создается впечатление, что как будто в центре пространства скоростей действует некоторое гравитационное поле, которое приводит к экспоненциальному умень­шению числа молекул с удалением от начала координат, подобно то­му, как это имеет место в земной атмосфере, где число молекул воздуха с высотой убывает по экспоненциальному закону.

Естественно никакого такого поля нет. Есть только изолиро­ванная, находящаяся в равновесии при температуре Т, система молекул, на которую не действуют внешние поля. Неоднородное же распределение в пространстве скоростей возникает в результате действия законов сохранения энергии и импульса при столкновениях молекул. Эти законы служат причиной того, что две молекулы, находящиеся в разных точках пространства скоростей и имеющие разные скорости, после столкновения переходят во вполне определенные точки этого пространства. Как показывает детальный анализ столкновений, достижение периферийных областей пространства скоростей требует многих столкнове­ний, а вот переход из периферийных областей ближе к центру про­странства осуществляется практически при каждом столкновении.

Это приводит, во-первых, к уменьшению числа молекул в области больших скоростей, т. е. к уменьшению плотности числа молекул в периферийных районах и, во-вторых, к увеличению плотности моле­кул с малыми скоростями (рис.11, а; 12, а). Безусловно, законы сохранения действу­ют и в обычном пространстве. Однако в отсутствии силовых полей эти законы в принципе не запрещают молекулам достигать любой точки x, y, z пространства, что и приводит к однородному распре­делению газа.

Таким образом, экспоненциальный характер зависимости максвелловской объемной плотности вероятности от величины ско­рости является следствием ограничений, которые накладывают за­коны сохранения на изменения скоростей при столкновении молекул. Причем, если рассматриваемое пространство скоростей трехмерно, то все сказанное справедливо для функции (1.10.34), если же пространство скоростей одномерно, то для функции (1.10.33). Графики этих функций представ­лены на рис. 11. Поясним эти графики. Вероятность того, что некоторая молекула имеет скорость, заключенную в преде­лах от до , равна , т. е. равна заштрихованной площади на рис. 11, б. С другой стороны, та же вероят­ность равна отношению числа точек в вертикальной полоске (на рис. 11, а она заштрихована) к общему числу точек (молекул) N. Как видно из рис. 11, б, одномерная плотность вероятности 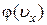от своего наибольше­го значения при убывает экспоненциально как в сторону по­ложительных, так и отрицательных проекций скоростей .

Теперь обратимся к функции . Функция (рис. 11, в), умноженная на элементарный объем , лежащий возле точки с координатами 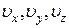пространства ско­ростей (на рис. 11, а он обозначен заштрихованным квадратиком), так же как и отношение числа точек , попавших в этот объем к общему числу точек N, дают вероятность того, что произвольно взятая молекула будет иметь величину скорости и направление движения, определяемые только местоположением объема dω. При этом из-за равновероятности направлений движения молекул в состоянии равновесия эта вероятность не может зависеть от направления на объем dω, а зависит только от расстояния υ до него. Поэтому вероятность попадания скоростной точки в каждый из трех заштрихованных на рис. 11, а квадратиков одна и та же. Эта вероятность равна заштрихованной области на рис. 11, в.

Функция распределения молекул по абсо­лютным значениям скорости. Величина (на рис. 12, б она равна заштрихованной площади) представляет собой вероятность того, что скорость произвольно взятой молекулы заключена в интервале независимо от ее направления движения. С другой стороны, эта вероятность, очевидно, может быть найдена, как отношение числа скоростных точек , попавших в заштрихованную на рис. 12, а область, к общему числу N скоростных точек. График функции 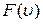(рис. 12, б) имеет существенно иной вид, нежели функций и 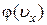: в окрестности точки 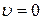функция , хотя плотность распределения по компонентам ско­рости в точке принимает наибольшее значение. Это объясняется тем, что, как видно из соотношения , объем шарового слоя, на который умножается функция , мал в окрестности точки .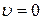

Закон Максвелла о распределении молекул по величине скорости

(1.11.1)

состоит из произведения двух конкурирующих множителей, зависящих от скорости: один из них с ростом увеличивается, а другой – уменьшается. При малых значениях возрастание первого множителя превосходит убывание второго, поэтому функция 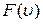вначале возрастает (рис. 12, б) с ростом . При больших значениях , наоборот, убывание второго множи­теля превосходит возрастание первого и функция 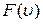в результате убывает с ростом . Таким образом, функция 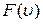с ростом сначала воз­растает, а затем убывает, поэтому при некотором значении она достигает наибольшей величины. Значение скорости, при которой функция 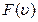максимальна, находится из уравнения 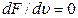. Дифферен­цирование дает

Значения и доставляют наименьшие значения функции 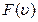, равные нулю. Значение скорости, обеспечивающее наибольшее значе­ние , находится из равенства и называется наиболее вероятной ско­ростью :

(1.11.2)

При этом максимальное значение функции 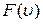равно:

(1.11.3)

Вероятность того, что величи­на скорости молекулы заключена в пределах от до , равна

(1.11.4)

и изображается на рис. 13 заштрихованной площадью. Так как, по

Рис. 13

определению вероятности, , где – число молекул, которые имеют скорость, заключенную в интервале 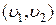, а N – общее число молекул, то выражение (1.11.4) можно представить в виде:

Число молекул, которые имеют скорость превышающие некоторое значение ,

(1.11.5)

Нетрудно показать, что площадь под графиком функции 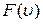и осью равна единице.

(1.11.6)

Таким образом, . Это известное условие нормировки функции 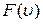, выполняемое для любой плотности вероятности, означает, что вероят­ность того, что молекула имеет какую-нибудь скорость, равна единице.

Так же легко показать, что среднее значение скорости молекул

(1.11.7)

Аналогично, можно найти выражение для среднего квадрата скорости:

(1.11.8)

Корень квадратный из среднего квадрата скорости называют средне­квадратичной скоростью молекул и обозначают . Таким образом,

(1.11.9)

Для характеристики чаще всего реализуемого в равновесном газе значения скорости молекул можно взять либо наиболее вероят­ную (1.11.2), либо среднюю (1.11.7), либо среднеквадратичную (1.11.9) скорости. Ни одна из них, как характеристика некоторого среднего, ориентировочного значения скорости молекул, возле которой группируются все возмож­ные значения, не может иметь предпочтения перед другими. К тому же все они дают близкие друг к другу значения. В самом деле, из сравнения (1.11.2), (1.11.7) и (1.11.9) нетрудно получить, что .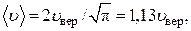

Важной особенностью закона Максвелла 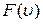является наличие ве­личины под знаком экспоненты, которая равна отношению кинетичес­кой энергии молекулы к кинетической энергии , соответствующей наиболее вероятной скорости молекулы.

Функция 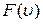является двухпараметрической, т. е. она содержит два параметра: массу молекулы и температуру газа Т.

Как видно из формулы (1.11.2), при повышении температуры газа максимум функции 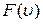сдвигается в сторону больших скоростей, высота же макси­мума при этом уменьшается, естественно, площадь под кривой 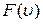и осью остается по-прежнему равной единице. На рис. 14 представлены два распределения по скоростям одного и того же газа при различ­ных температурах . Как видно, с повышением температуры увеличи­вается число молекул с большими скоростями и уменьшается число молекул с малыми скоростями.

Рис. 14 Рис. 15