Модель идеального газа.

Наиболее простой теоретической моделью газа является идеальный газ. В этой модели пренебрегают размерами и взаимодействиями молекул и учитывают лишь их упругие столкновения. Более реальной является расширенная модель идеального газа, в которой молекулы представляются упругими сферами с конечным диаметром d, а взаимодействие по-прежнему учитывается только при непосредственном упругом столкновении молекул.

Определим критерий идеального газа. Ясно, что газ будет идеальным, если расстояние rмежду его молекулами такое, что силой взаимодействия между ними можно пренебречь. Силы взаимодействия между молекулами быстро убывают с расстоянием r и уже на расстоянии несколько диаметров d молекулы пренебрежимо малы. Поэтому условие идеальности газа в расширенном понимании можно записать в виде

r >> d. (1.1.1)

Расстояние r нетрудно выразить через такой важный параметр газа, как концентрацию n = N/V, здесь N – число частиц в газе, а V – его объем. В самом деле, если газ находится в равновесии при отсутствии внешних полей, то, как показывает опыт, его молекулы будут равномерно распре­делены в объеме V м³ , и тогда на ребре куба длиной 1 м расположится 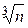молекул. Следовательно, среднее расстояние между молекулами составит

. (1.1.2)

Из соотношений (1.1.1) и (1.1.2) следует, что критерий идеальности газа можно представить следующим образом:

nd ³<< 1, (1.1.3)

где nd ³ – безразмерный параметр.

Учитывая, число частиц в газе N = mN_A/m, концентрацию можно выразить через плотность r газа:

(1.1.4)

где r = m/V – плотность газа.

Выражение (1.1.4) позволяет записать критерий идеальности газа (1.1.3) в эквивалентной форме:

rN_Ad³/m << 1. (1.1.5)