
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Некоторые теоремы теории вероятности. (Теоремы сложения и умножения вероятностей. Условие нормировки вероятностей.)
Определение: Суммой С = А + В двух событий А и В называется событие С, состоящее в появлении хотя бы одного из событий А или В.
Теорема 1. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий, т. е.
| (А3) |
Р(А+В)=Р(А)+Р(В).
Доказательство проведем для событий, составляющих схему случаев.
Пусть возможные исходы опыта сводятся к совокупности случаев, которые мы для наглядности изобразим в виде n точек.

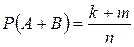
С л е д с т в и е 1. Если события А1,..., Аn образуют полную группу несовместных событий, то сумма их вероятностей равна единице
| (А7) |

О п р е д е л е н и е. Противоположными событиями  и
и 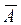 называют два несовместных события, образующих полную группу.
называют два несовместных события, образующих полную группу.
Сумма вероятностей противоположных событий на основании следствия 1, очевидно, равна единице, т. е.
| (А10) |
 .
.
О п р е д е л е н и е. Событие А называют независимым от событияВ, если вероятность события А не зависит от того произошло событие В или нет, т. е.
| (А11) |
Р(А/В) = Р(А).
В выражении (А11) Р(А/В) – есть вероятность события А при условии, что событие В имело место. Говорят, что Р(А/В) условная вероятность события А.
О п р е д е л е н и е. Произведением двух событий А и В называется событие, состоящее в совместном (или одновременном) появлении этих двух событий.
Теорема 2. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие имело место:
| (А12) |
Р(А, В) = Р(А)Р(В/А).
Докажем теорему 2 для событий, сводящихся к схеме случаев. Пусть возможные исходы опыта сводятся к n случаям, которые изобразим в виде точек

| (А13) |

 .
.
Вычислим Р(В/А), т. е. условную вероятность события B в предположении, что А имело место. Если известно, что событие А произошло, то из ранее возможных n случаев остаются возможными только те m случаев, которые благоприятствовали событию А. Из них l случаев благоприятны событию В. Поэтому
| (А14) |
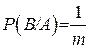 .
.
Подставляя (А13) и (А14) в (А12) получим тождество. Теорема доказана.
С л е д с т в и е 1. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий.
Следствие 1 непосредственно вытекает из определения независимости событий Р(В/А) = Р(В) и теоремы 2.
8. Интегральная функция распределения. Случайные величины. Интегральная функция распределения случайной величины и её свойства.
О п р е д е л е н и е. Случайной величиной Х называют величину, которая в результате опыта принимает то или иное значение, заранее неизвестно какое.
О п р е д е л е н и е. Интегральной функцией распределения Ф(х) называется вероятность того, что случайная величина Х примет значение меньшеех, т. е.
| (А15) |
 .
.
Свойства функцииФ(x):
1. Функция Ф(х) – неубывающая функция своего аргумента, т. е. если х2 > х1, то 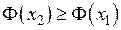 .
.
| (А16) |
2. 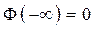 .
.
| (А17) |
3.  .
.
4. Вероятность того, что случайная величина Х примет значение на интервале от 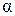 до
до 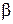 , равна приращению функции на этом интервале,
, равна приращению функции на этом интервале,
т. е.
| (А18) |

5.  .
.
9. Плотность вероятности и её свойства.
По определению производной интегральной функции распределения

| (А19) |
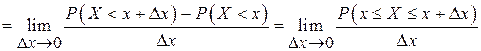 .
.
В числителе правой части последнего выражения стоит вероятность, что случайная величина примет значение на интервале Δх, лежащем возле точки х. Ясно, что эта вероятность зависит от того, где взять эту точку х, т. е.
 .
.
Если эту величину разделить на Δх и устремить Δх к нулю, то получим плотность вероятности (по аналогии линейной плотности массы, “размазанной” по оси х) случайной величины Х в точке х. Таким образом, если обозначить плотность вероятности ω(х), то из (А19)
| (А20) |
 .
.
Отметим некоторые полезные свойства плотности вероятности ω(х).
1. 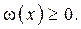
2.  .
.
3. Чтобы найти вероятность принять случайной величине значение из интервала ( 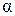 , β), необходимо проинтегрировать плотность ω(х) на этом интервале, т. е.
, β), необходимо проинтегрировать плотность ω(х) на этом интервале, т. е.
| (А22) |
 .
.
Дата добавления: 2015-04-18; просмотров: 507; Мы поможем в написании вашей работы!; Нарушение авторских прав |