
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Средние значения случайных величин. (математическое ожидание). Среднее по времени и среднее по ансамблю. Эргодическая гипотеза (без доказательства).
Среднее значение является важнейшей, хотя и грубой, характеристикой случайной величины X. Она характеризует среднее, ориентировочное значение, около которого группируются все возможные значения случайной величины. Чтобы установить правило, по которому её вычисляют, рассмотрим сначала дискретную случайную величинуX, характеризуемую рядом распределения
| xi | x1 | x2 | … | xn |
| P(xi) | P(x1) | P(x2) | … | P(xn) |
где xi – возможные значения, которые принимает на опыте случайная величина X, а P(xi) – их вероятности появления.
Пусть произведено большое число N измерений случайной величины Х так, что значение x1 было наблюдено т1 раз, х2 – m2 раз,...xn – mn раз. При этом
 .
.
Среднее арифметическое наблюдаемых значений случайной величины X равно:
| (А23) |
 ,
,
где  - величина, характеризующая, как часто принимает в опыте значение xi случайная величина X. Величину
- величина, характеризующая, как часто принимает в опыте значение xi случайная величина X. Величину 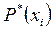 называют частотой события xi. Дальше будет доказано, что частота
называют частотой события xi. Дальше будет доказано, что частота 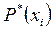 с вероятностью почти единица (т. е. достоверно) равна вероятности
с вероятностью почти единица (т. е. достоверно) равна вероятности  , если только число опытов
, если только число опытов  (Теорема Бернулли). С учётом этой теоремы равенство (А23) можно переписать в виде:
(Теорема Бернулли). С учётом этой теоремы равенство (А23) можно переписать в виде:
| (А24) |
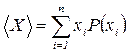 .
.
Величину (А24) называют средним значением случайной величины Х и обозначают . Таким образом, среднее значение дискретной случайной величины Х равно сумме произведений каждого из ее возможного значения xi на его вероятность Р(хi).
. Таким образом, среднее значение дискретной случайной величины Х равно сумме произведений каждого из ее возможного значения xi на его вероятность Р(хi).
В случае непрерывной случайной величины Х нетрудно получить аналогичное выражение для вычисления ее среднего значения:
| (А25) |
 .
.
Свойства среднего значения
1. Среднее от неслучайной величины c = const равно значению этой величины, т. е.
 (A.30)
(A.30)
2. Еcли с - неслучайная величина, а X - случайная, то
 , (A.31)
, (A.31)
т. е. постоянную можно выносить за знак среднего значения.
3. Среднее от суммы двух случайных величин равно сумме иx средних значений, т. е.
áX + Yñ = áXñ + áYñ. (A.32)
4. Среднее от произведения двух независимых случайных величин равно произведению их средних значений.
 . (A.37)
. (A.37)
Весьма существенно, что это равенство имеет место только для независимых случайных величин.
11. Дисперсия и её свойства.
Для характеристики рассеивания возможных значений случайной величины около ее среднего значения вводится дисперсия, которая представляет собой среднюю квадратическую разность между значениями случайной величины и ее средним значением, т. е.
 . (А.38)
. (А.38)
По определению среднего для дискретных случайных величин
 , (A.39 а)
, (A.39 а)
где введено обозначение  , а для непрерывных величин
, а для непрерывных величин
 . (A.39 в)
. (A.39 в)
Таким образом, дисперсия случайной величины X равна среднему квадрату этой величины минус квадрат ее среднего.
Для характеристики рассеивания более целесообразно взять величину, которая имеет размерность самой случайной величины, а не ее квадрата. Поэтому в рассмотрение вводят среднее квадратическое отклонение sx, которое равно корню квадратному из дисперсии:
 . (A.42)
. (A.42)
Основные свойства дисперсии:
1. Дисперсия постоянной величины c = constравна нулю.
2. Неслучайная величина c = constвыносится из-под знака дисперсии
в квадрате:
 . (A.44)
. (A.44)
для среднего квадратичного отклонения:
 .
.
3. Дисперсия суммы двух независимых случайных величин равна
сумме их дисперсий:
 . (A.45)
. (A.45)
Для независимых случайных величин:
 . (A.46)
. (A.46)
Подчеркнем, что формулы (A.45) и (A.46) имеют место только для независимых величин.
Дата добавления: 2015-04-18; просмотров: 391; Мы поможем в написании вашей работы!; Нарушение авторских прав |