Основное уравнение молекулярно-кинетической теории газов для давления. (Давление ИГ с точки зрения МКТ.)

Рассмотрим N молекул газа находящихся в состоянии равновесия в сосуде объема V, при этом их концентрация n = N/V. Давле­ние газа определяется суммой нормальных составляющих всех сил, с которыми действуют отдельные молекулы на единичную площадь стенки.

Р и с. 10

Для вычисления этого давления возьмем на стенке сосуда площадку dS и направим ось Z перпендикулярно ей, так что эта площадка будет лежать в плоскости XOY, перпендикулярной плоскости рис. 10. Пусть некоторая молекула падает на площадку dS под углом θ к оси Z. При упругом ударе молекула зеркально (θ₁= θ₂) отразится от площадки dS, сохраняя величину скорости υ неизменной (υ₁ = υ₂= υ).

По третьему закону Ньютона сила , действующая со стороны стенки на молекулу, равна по величине и противоположна по направлению силе – , с которой молекула действует на стенку.

(1.5.3)

Чтобы найти число молекул, ударяющихся о площадку dS за время dt под углами от θ до θ+ dθ и имеющих скорости от υ до υ + dυ, необходимо проинтегрировать соотношение (1.4.4) предыдущего параграфа по всем возможным углам φ (от φ = 0до φ = 2π), т. е.

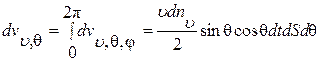(1.5.4)

Эти молекулы сообщают площадке dS за время dt импульс силы

(1.5.5)

Подставляя сюда из выражений (1.5.3) и (1.5.4) величины 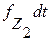и , имеем

. (1.5.6)

Чтобы учесть все молекулы, ударяющиеся о площадку dS с различными скоростями υ и под различными углами θ, необходимо последнее соотношение проинтегрировать по υ от нуля до υ_max и по θ от нуля до π/2, т. е.

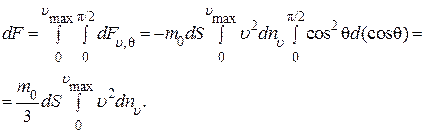(1.5.7)

Разделив обе части равенства (1.5.7) на площадь dS, получим выражение для давления, производимого газом на стенку сосуда:

(1.5.8)

Вводя в правую часть выражения (1.5.8) постоянную величину, равную концентрации n молекул в сосуде, получим

(1.5.9)

где ρ = m₀n – плотность газа, а – средний квадрат скорости молекулы газа. Формуле (1.5.9) можно придать следующий вид:

(1.5.10)

где – кинетическая энергия поступательного движения молекулы, среднее значение которой

(1.5.11)

Функция распределения по кинетическим энергиям связана с функцией по скоростям молекул соотношением (см. A.71 прил. А)

(1.5.12)

Таким образом, давление (1.5.10), создаваемое молекулами газа, равно двум третям средней кинетической энергии поступательного движения всех молекул, имеющихся в единичном объеме.

Как видно из выражений (1.5.9)–(1.5.11), давление P зависит от вида функции распределения (или ).

Нахождение функций распределения равновесных (и неравновесных) состояний системы частиц является основной задачей статистической физики.