Теорема о равномерном распределении энергии теплового движения по степеням свободы. Число степеней свободы молекул. Средняя энергия теплового движения молекул газа.

Большинство химических веществ состоит из многоатомных моле­кул. Если рассматривать газообразное состояние вещества, то при столкновениях молекул тепловая энергия газа случайным образом расходуется на изменение кинетических энергий поступательного и вращательного движений молекул, а также на возбуждение колебаний атомов в молекуле. Естественно предположить, что указанные движения в молекуле могут происходить одновременно.

Чтобы найти среднюю энергию молекулы, приходящуюся на все виды ее движения, сначала выясняют, каким числом степеней свободы обладает данная молекула, и далее, – какая энергия приходится в среднем на одну степень свободы.

Число степеней свободы i молекулы равно количеству независимых координат, определяющих ее положение относительно выбранной системы координат.

Если рассматривать атомы как бесструктурные точки, то одно­атомные молекулы могут иметь только энергию поступательного движе­ния. Число степеней свободы каждой такой точки i_пост = 3 (три декартовы координаты x, y, z или три сферические 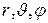определяют положение одноатомной молекулы в пространстве). Система, состоящая из N одноатомных молекул, между которыми нет жестких связей, имеет 3N степеней свободы.

Двухатомную молекулу представим как систему, состоящую из двух материальных точек. Если расстояние r между атомами в молекуле не изменяется (атомы в молекуле не колеблются и с увеличением час­тоты вращения молекула не растягивается), то число степеней свободы равно пяти. В самом деле, если расстояние между атомами 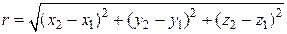, где 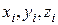– координаты i-го атома в молекуле (i = 1, 2), фиксировано, то всего имеется пять независимых координат, шестая определяется из последнего соотношения. Положение двухатомной молекулы, состоящей из двух жестко связанных атомов, задают обычно не пятью декартовыми координатами, а тремя координатами центра С (x, y, z) масс молекулы и двумя углам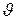и и 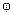, определяющих направление в пространстве прямой, проходящей через два атома молекулы. Есл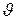и и 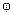неизменны, а изменяются координаты центра масс, то это указывает на то, что молекула движется поступательно. Это дает три поступательные степени свободы (i_пост = 3). Изменение же углов 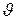и 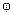при фиксированных координатах центра масс определяет вращение молекулы вокруг двух взаимно перпендикулярных осе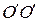й и 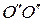, проходящих через центр масс, и перпендикулярных оси ОО молекулы (рис. 20).

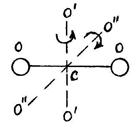
Р и с. 20

Вращение молекулы вокруг оси ОО не учитывают, так как энергия этого вращения значительно меньше двух других (из-за малости моментов инерции атомов). Поэтому у двухатом­ной молекулы две вращательные степени свободы, т. е. 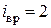. Если расстояние между атомами в молекуле меняется, то это означает, что атомы колеблются друг относительно друга. В этом случае у двухатомной нежесткой молекулы имеется шесть степеней свободы ( ).

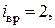
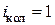Если число атомов в молекуле , то по динамическим свой­ствам их делят на линейные (типа молекул HCN, CO₂ рис. 21) и нелинейные (например, молекула воды H₂O).

Р и с. 21

В линейных молекулах, в отличие от нелинейных, атомы расположены вдоль одной прямой. Поэтому жесткая линейная молекула содержит столько же степеней свободы, сколько имеет жесткая двухатомная, т. е. пять. Нелинейная жесткая молекула, очевидно, имеет, как и твердое тело, шесть степеней свободы.

Нелинейные молекулы имеют 3n –6 колебательных степеней свободы, так как из общего числа 3n степеней свободы три относятся к поступательному и три к вращательному движению. У линейной моле­кулы существуют две степени свободы вращательного и три поступательного движения, поэтому для нее число колебательных степеней свободы 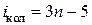. Можно доказать, что произвольное колебательное движение атомов в нелинейной молекуле всегда можно представить в виде суммы 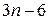простейших так называемых нормальных колебаний (и для линейной молекулы). Нормальное колебание – гармоническое, при котором все ядра атомов в молекуле колеблются с одной и той же частотой и одинаковой фазой, т. е. одновременно проходят через положение равновесия. На рис. 22 показаны нормальные колебания молекулы 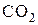. Стрелки показывают направление скорости при колебаниях атомов и приблизительно величину амплитуды (длина стрелки).

Два нижних колебания вырождены, т. е. имеют одинаковую частоту.

Р и с.22

Кинетическая энергия одноатомной молекулы, имеющей три степени свободы, равна

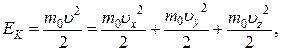(1.17.1)

т. е. содержит столько слагаемых, сколько у нее степеней свободы. Чтобы определить, какая в среднем энергия приходится на одну степень свободы, усредним обе части выражения (1.17.1).

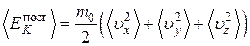. (1.17.2)

Из формул (1.10.31) – (1.10.32) следует, что

. (1.17.3)

Умножая обе части равенств (1.17.3) на , получим

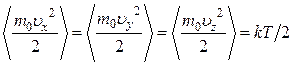. (1.17.4)

Таким образом, на каждую степень свободы одноатомной молекулы приходится энергия, равная 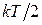. Подстановка (1.17.4) в (1.17.2) дает среднюю кинетическую энергию поступательного движения одноатомной молекулы:

. (1.17.5)

Жесткая нелинейная молекула имеет три поступательные и три вращательные степени свободы, поэтому ее кинетическая энергия содержит шесть слагаемых.

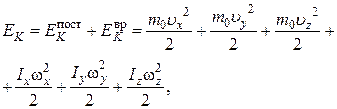(1.17.6)

где 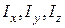– моменты инерции молекулы относительно трех декартовых осей координат, проходящих через центр инерции молекулы; 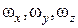– проекции угловой скорости вращения молекулы на те же оси координат. Аналогичное выражение можно записать для средних величин:

(1.17.7)

Установим, какая в среднем энергия приходится на одну вращательную степень свободы. Для этого, как видно из последнего выражения, необходимо вычислить средние квадраты угловой скорости

(1.17.8)

где 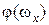– функция распределения молекул по проекции угловой скорости. Функция 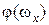должна иметь такой же вид, как распределение Максвелла 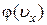, ибо для нахождения 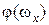полностью применимы такие же рассуждения, какие были сделаны при выводе 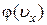. При этом нужно учесть, что при вращательном движении роль массы выполняет момент инерции, а поступательная скорость 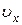заменяется угловой 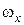. Поэтому

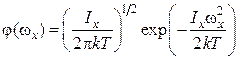. (1.17.9)

Подставляя (1.17.9) в (1.17.8) и выполняя интегрирование, находим

(1.17.10)

Аналогично получаем

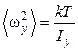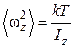; . (1.17.11)

Из выражений (1.17.9) и (1.17.10) находим

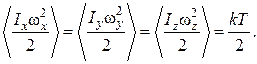(1.17.12)

Таким образом, на каждую вращательную степень свободы приходится такая же энергия 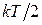, как и на поступательную. При этом кинетическая энергия, которой обладает жесткая нелинейная молекула, согласно выражения (1.17.7), равна

. (1.17.13)

Если в многоатомной молекуле возбуждены колебания атомов (это наблюдается при температурах значительно больших комнатных), то на каждое нормальное колебание молекулы приходится энергия в два раза большая, чем на поступательную или вращательную степень свободы. Это связано с тем, что при гармонических колебаниях, как известно из механики, среднее значение кинетической энергии равно среднему значению потенциальной энергии; если на одну степень свободы поступательного движения приходится кинетическая энергия 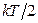, то такая же энергия 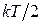падает и на потенциальную энергию. Поэтому тепловая энергия, приходящаяся на одну колебательную степень свободы молекулы, равна

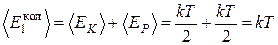. (1.17.14)

Закон равнораспределения тепловой энергии по степеням свободы: если система молекул находится в равновесном газообразном состоянии, то средняя кинетическая энергия, приходящаяся на каждую поступательную, вращательную и колебательную степени свободы его молекул, равна 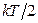, средняя потенциальная энергия, приходящаяся на каждое нормальное гармоническое колебание атомов в молекуле, также равна .

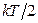Закон равнораспределения применим к идеальному газу. Если же газ находится при больших давлениях, то при вычислении полной энергии газа E необходимо учитывать энергию взаимодействия молекул между собой.