Изобарный процесс

Параметры состояния идеального газа на изобаре связаны соотноше-нием (1.9.7):

Отсюда видно, что чем выше температура газа, тем больше его объем. При этом величина объема на изобаре при повышении температуры растет тем быстрее, чем меньше давление.

Для реальных газов, жидкостей и твердых тел при нагревании также увеличивается объем на изобаре, (за исключением аномальных областей состояний четырех веществ: лед, германий, висмут, сурьма). Для характеристики термического расширения вещества при его изобарном нагревании вводят в рассмотрение коэффициент объемного расширения

. (2.7.5)

Как видно из формулы (2.7.5), коэффициент 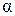численно равен увели­чению объема вещества, взятого в количестве , при его изобарном нагревании на 1К. В частности, используя уравнение 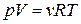нетрудно получить, что для идеального газа коэффициент 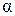равен:

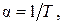(2.7.6)

т. е. приращение объема идеального газа при его изобарном нагревании уменьшается с ростом температуры.

Известно, что коэффициент 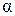для газов, значительно больше, чем для жидкостей и твердых тел.

Работа системы в изобарном процессе равна

(2.7.7)

Для идеального газа последнее выражение, очевидно, может быть пере-писано еще в одном виде:

. (2.7.8)

Количество теплоты, получаемое системой при нагревании (или отдаваемое системой при охлаждении) в изобарном процессе может быть найдено из первого закона термодинамики:

(2.7.9)

где – энтальпия или тепловая функция. Энтальпия является функцией состояния, так как и 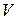– функции состояния. Измеряется энтальпия в джоулях.

Интегрируя выражение от состояния до состояния , получим

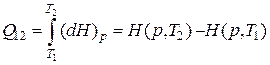. (2.7.10)

Таким образом, количество теплоты, получаемое системой при ее изобарном нагревании от состояния до состояния , равно разности энтальпий в этих состояниях.

Рассматривая энтальпию как функцию T и p, т. е. мо-жем записать

. (2.7.11)

Откуда следует, что

. (2.7.12)

В определение теплоемкости вещества при постоянном давлении

вместо подставим его выражение из (2.7.9). В результате будем иметь

. (2.7.13)

Из соотношений (2.7.13) и (3.7.12) следует, что

. (2.7.14)

Отсюда видно, что теплоемкость характеризует скорость роста энтальпии Н при повышении температуры Т.

Проинтегрируем (2.7.12) от состояния до состояния .

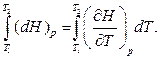(2.7.15)

Учитывая выражения (2.7.10) и (2.7.14), последнее равенство можно переписать в виде

(2.7.16)

Если теплоемкость не зависит от температуры, то количество теплоты в изобарном процессе

(2.7.17)

Заметим, что энтальпия для идеального газа

(2.7.18)

и, таким образом, не зависит от давления, так же как и внутренняя энергия