Цикл Карно и его КПД.

Цикл Карно является обратимым циклическим процессом с двумя источниками теплоты, имеющими разные, но постоянные температуры. Так как температуры источников тепла постоянные, а процессы получения и отдачи рабочим веществом тепла должны быть обратимыми, то эти процессы могут быть только изотермическими. При этом температура рабочего вещества в цикле должна, очевидно, меняться без теплообмена с окружающей средой, т.е. в адиабатных условиях. Поэтому цикл Карно состоит из двух обратимых изотермических и двух обратимых адиабатных процессов, чередующихся между собой.

Цикл Карно осуществляется рабочим веществом следующим образом (рис. 37).

Р и с. 37

Рабочее вещество, расширяясь изотермически от состояния 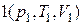до состояния , получает количество тепла от горячего источника, имеющего температуру на бесконечно малую величину большую, чем температура рабочего вещества (обратимость), т. е. . При этом, если в качестве рабочего вещества взять идеальный газ, то он производит работу (2.7.22), равную количеству полученного тепла :

. (2.11.1)

В состоянии 2 к рабочему веществу прекращается подвод тепла и затем в обратимом адиабатном процессе расширения до объема температура рабочего вещества уменьшается до температуры 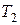, которая на бесконечно малую величину больше температуры холодного источника Далее рабочее вещество изотермически обратимо сжимается от объема до объема . При этом рабочее вещество (идеальный газ) отдает холодному источнику коли-чество тепла

. (2.11.2)

Откуда находим

. (2.11.3)

Наконец, замыкающим цикл процессом является обратимый адиабатный процесс, в котором рабочее вещество возвращается в начальное состояние 1.

Вычислим КПД цикла Карно. По определению КПД любого цикла

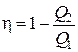. (2.11.4)

Подставляя выражения (2.11.1) и (2.11.3) в (2.11.4), получим

(2.11.5)

Из последнего выражения видно, что КПД цикла не зависит от количества рабочего вещества . Уравнение адиабаты идеального газа 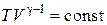запишем для двух адиабатных процессов 23 и 41:

(2.11.6)

. (211.7)

Откуда находим

(2.11.8)

Подставив последнее выражение в (2.11.5), будем иметь:

(2.11.9)

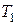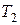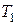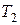Таким образом, КПД цикла Карно, произведенного с идеальным газом, определяется только температурами (горячего) и (холодного) источников тепла. При этом тем больше, чем больше разность между и . КПД цикла Карно равен 1 в двух практически недостижимых случаях: когда или, когда 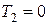. Если КПД цикла равен единице, то из выражения (2.11.4) следует, что , т. е. все тепло , полученное от горячего источника, преобразуется в работу, что запрещено вторым началом термодинамики. Следовательно, КПД никакого цикла, в том числе и цикла Карно, не может быть равен единице.

44. Теоремы Карно. КПД цикла Карно – верхний предел КПД тепловых машин.

Формула (2.11.9) для КПД цикла Карно получена в предположении, что рабочим веществом являлся идеальный газ. Однако эта формула верна для любых рабочих веществ, используемых в цикле Карно, что доказывает следующая теорема.

Первая теорема Карно. КПД обратимого цикла Карно, осуществляемого между двумя источниками теплоты, не зависит от свойств рабочего вещества, с помощью которого этот цикл осуществляется.

Рассмотрим два тепловых двигателя, работающих между одними и теми же горячим и холодным источниками, но с разными рабочими веществами. Оба двигателя работают по обратимым циклам Карно. Пусть каждый из тепловых двигателей отбирает от горячего источника за цикл одно и тоже количество тепла, равное . Этого всегда можно добиться, т. к. КПД теплового двигателя не зависит от количества рабочего вещества. Если задано количество рабочего вещества, участвующего в цикле в одном из двигателей, то всегда можно подобрать количество рабочего вещества в другом двигателе таким, чтобы количество теплоты, отбираемое первым и вторым двигателями было одинаковым, т. е. (см. 2.11.1). Тогда КПД этих двигателей будут равны:

(2.12.1)

(2.12.2)

Доказательство теоремы будем вести от противного. Предположим, что КПД этих двигателей не равны, к примеру, пусть . На основании формул (2.12.1–2.12.2) это означает, что первый двигатель за цикл производит большую работу и отдает холодному источнику меньше тепла, чем второй двигатель, т. е. при и Так как циклы обоих двигателей обратимы, включим первый двигатель в прямом, а второй – в обратном направлениях (рис. 38).

Р и с. 38

Тогда работа, производимая первым двигателем, согласно формуле (2.9.6)

(2.12.3)

а работа, потребляемая от первого двигателя вторым,

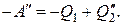(2.12.4)

Просуммируем левые и правые части равенств (2.12.3–2.12.4). В результате будем иметь:

(2.12.5)

так как и

Таким образом, в результате совместной работы двух двигателей состояние горячего источника не изменилось (первый двигатель за цикл отнял у него количество тепла , второй двигатель за цикл вернул такое же количество тепла), холодный же источник отдал за цикл количество тепла и за счет этого тепла, согласно формуле (2.12.5), совершена положительная работа.

Этот вывод противоречит второму закону термодинамики в формулировке Кельвина. Поэтому предположение, что неверно.

Остается предположить, что . В этом случае, включив второй двигатель в прямом, а первый – в обратном направлении, и, проведя аналогичные рассуждения, придем к выводу, что возможен вечный двигатель второго рода. Следовательно, и это предположение неверно. Остается единственный вариант Таким образом, теорема Карно доказана.

Из этой теоремы следует, что формула (2.11.9), полученная для идеального газа, справедлива для любых рабочих веществ, осуществля-ющих обратимый цикл Карно.

Вторая теорема Карно. КПД необратимого цикла Карно всегда меньше обратимого цикла Карно, осуществляемого между одними и теми же источниками теплоты, имеющими постоянные, но разные температуры.

Для доказательства воспользуемся формулой (2.11.9):

(2.12.6)

Рассмотрим прямой обратимый цикл Карно. Как мы знаем, чтобы в прямом цикле рабочее вещество обратимо получало тепло и расширялось по изотерме 12 (рис. 37), его температура 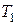должна быть на бесконечно малую величину меньше температуры горячего источника , т. е.

(2.12.7)

Чтобы рабочее вещество обратимо отдавало тепло при сжатии (на изотерме 34), его температура 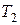должна быть на бесконечно малую величину больше температуры холодного источника , т. е.

(2.12.8)

Подставляя выражения (2.12.7–2.12.8) в (2.12.6) и пренебрегая бесконеч-но малыми, получим КПД обратимого цикла Карно равен

. (2.12.9)

Для необратимого прямого цикла Карно разности между температурами источников теплоты и рабочего вещества имеют конечное значение:

, (2.12.10)

. (2.12.11)

При этом интервал температур рабочего вещества сужается (поскольку 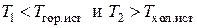), что приводит, естественно, к уменьшению КПД цикла Карно. Подставляя (2.12.10–2.12.11) в (2.12.6), получаем, что КПД необратимого цикла Карно

. (2.12.12)

Сравнивая соотношения (2.12.9) и (2.12.12), заключаем, что

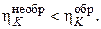(2.12.13)

Неравенство (2.12.13) получено с учетом одной только внешней необратимости цикла Карно – конечной разности температур между рабочим веществом и источником теплоты. В реальных циклах имеются и внутренние необратимости циклов: процесс трения (при этом часть полезной работы за цикл тратится на трение, что уменьшает КПД цикла), отсутствие механического равновесия (в этом случае давление газа на конечную величину больше или меньше внешнего давления среды) и другие. Все эти необратимости в цикле Карно приводят к уменьшению полезной работы, а, значит, к еще большему усилению неравенства (2.12.13). Следовательно, и вторая теорема Карно доказана.

Третья теорема Карно. Обратимый цикл Карно имеет наибольший КПД по сравнению с любыми обратимыми или необратимыми циклами, в которых наибольшая и наименьшая температуры равны соответственно температуре горячего источника и температуре холодного источника цикла Карно.

Рассмотрим произвольный обратимый цикл, в котором температура рабочего вещества изменяется произвольным образом. В этом случае его невозможно провести обратимо, располагая только двумя источниками тепла с постоянными температурами. Если в начальном состоянии температура рабочего вещества и будет отличаться от температуры источника на бесконечно малую величину, то при дальнейшем изменении температуры рабочего вещества она может оказаться больше (или меньше) температуры источника тепла на конечную величину, что приведет к необратимому процессу теплопроводности и сам процесс станет необратимым. Поэтому для того, чтобы произвольный цикл был обратим, необходимо располагать бесконечно большим числом источников тепла, температуры которых отличаются на бесконечно малую величину.

Введение в теоретическую схему множества источников тепла производится для произвольного цикла следующим образом (рис. 39):

Р и с. 39

Проведем через этот обратимый цикл адиабаты, бесконечно близко расположенные друг к другу. При этом линии и процесса разобьются на бесконечно малые отрезки, через середины которых проведем изотермы, которые соединят ближайшие адиабаты. В результате таких манипуляций весь цикл разобьется бесконечно узкими циклами Карно. На каждом -м цикле рабочее вещество получает количество тепла от -го горячего источника, находящегося при температуре и отдает количество тепла -му холодному источнику, имеющему температуру . Совокупность элементарных циклов Карно вполне эквивалентна первоначальному произвольному циклу. В самом деле, поскольку каждая из адиабат, исключая две крайние, проходится в совокупности дважды и при этом в разных направлениях, суммарная работа цикла при замене его элементарными циклами Карно остается неизменной. Количество же тепла , получаемое процессом на линии , равно суммарному количеству тепла, получаемому в элементарных изотермах цикла Карно на том же пути , т. е.

, (2.12.14)

а отдаваемая теплота на линии 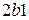будет равна:

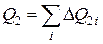. (2.12.15)

Таким образом, при бесконечно большом числе источников тепла, с которыми рабочее вещество обменивается теплом, произвольный цикл становится обратимым. При этом его КПД

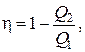(2.12.16)

где и определяются формулами (2.12.14–2.12.15).

КПД элементарного -го цикла Карно можно записать в виде:

(2.12.17)

Откуда находим

(2.12.18)

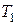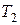Обозначим через и соответственно наибольшую и наименьшую температуры в произвольном обратимом цикле, т. е. и Так как и , то что можно переписать в виде:

. (2.12.19)

Просуммируем левую и правую части равенства (2.12.18). В результате будем иметь

. (2.12.20)

В правой части последнего равенства заменим на меньшую величину От этого сумма может только уменьшиться, т. е.

. (2.12.21)

Подставляя в формулу (2.12.16) вместо меньшую величину , получим

(2.12.22)

Таким образом, КПД произвольного обратимого цикла не может быть больше КПД обратимого цикла Карно, протекающего между наибольшей температурой 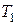и наименьшей температурой 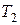этого произвольного цикла.

Если произвольный цикл необратим, то на основании второй теоремы Карно неравенство (2.12.22) еще более усилится, т. е.

(2.12.23)

Фундаментальное значение доказанной теоремы состоит в том, что она устанавливает наибольший предел КПД тепловых двигателей, к которому должен стремиться инженер-теплотехник в своей исследова-тельской работе.

В заключение этого параграфа отметим, что обратимый цикл Карно с точки зрения количества необходимых источников теплоты является предельно экономным: для его осуществления достаточно всего лишь двух источников тепла с постоянными, но разными температурами, так как подвод теплоты к рабочему веществу от горячего источника и отдача теплоты от рабочего вещества холодному источнику происходят по изотермам.

Равенство Клаузиуса. Энтропия. Свойства энтропии. Математическое выражение второго начала термодинамики для обратимых процессов. Постоянство энтропии при обратимых процессах в замкнутой системе.

По определению КПД любого цикла

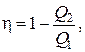(2.13.1)

а обратимого цикла Карно

(2.13.2)

Из выражений (2.13.1–2.13.2) следует, что

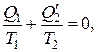(2.13.3)

где Отношение количества теплоты, получаемой (отдаваемой) системой, к абсолютной температуре, при которой эта теплота получена (отдана) Клаузис назвал приведенной теплотой. Равенство (2.13.3) утверждает, что сумма приведенных теплот в обратимом цикле Карно всегда равна нулю, хотя сумма самих теплот в этом цикле не равна нулю, т. е.

Обобщим равенство (2.13.3) на любой обратимый цикл, совершаемый системой. Для этого, как мы это делали при доказательстве третьей теоремы Карно, разобьем этот цикл на элементарные циклы Карно, для каждого из которых будет справедливо равенство, подобное (2.13.3), т. е.

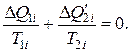(2.13.4)

Суммируя соотношение (2.13.4) по всем элементарным циклам Карно, будем иметь:

(2.13.5)

Переобозначив индекс суммирования, выражение (2.13.5) можно записать в виде одной суммы:

(2.13.6)

Если количества полученного и отданного тепла на изотермах элементарных циклов Карно считать бесконечно малыми, то выражение (2.13.6) можно представить в виде интеграла по замкнутому контуру:

(2.13.7)

Равенство (2.13.7) утверждает: сумма бесконечно малых приведенных теплот в любом обратимом круговом процессе всегда равна нулю. Это равенство является математическим выражением второго закона термодинамики для обратимых круговых процессов и называется равенством Клаузиуса.

Как отмечалось ранее, если интеграл по замкнутому контуру равен нулю, то подынтегральная функция есть полный дифференциал некоторой функции, которую обозначим буквой 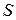, т. е.

(2.13.8)

Интегрируя последнее соотношение, получим

(2.13.9)

где 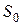– произвольная постоянная.

Если проинтегрировать выражение (2.13.8) от состояния 1 до состоя-ния 2, получим

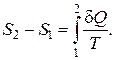(2.13.10)

Равенства (2.13.8) и (2.13.10) также представляют собой запись второго закона термодинамики для обратимых некруговых процессов. Как видно из формулы (2.13.10), функция S является функцией состояния. Ее называют энтропией.

Рассмотрим основные свойства энтропии.

1. Если система частиц совершает обратимый процесс и получает тепло , то ее энтропия, как видно из (2.13.8), увеличивается

2. Если система совершает обратимый процесс и при этом отдает тепло , то ее энтропия уменьшается

3. Если система адиабатически изолирована и совершает обратимый процесс, то ее энтропия не изменяется и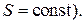

Если система замкнута, т. е. не обменивается с внешней средой энергией ни в форме тепла, ни в форме работы, то энтропия такой замкнутой системы также остается постоянной при любых совершающихся в ней обратимых процессах.

4. Увеличение температуры вещества при его нагревании ведет к росту его энтропии.

Если молей вещества поглощают 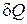теплоты и при этом его температура повышается на , то

(2.13.11)

Подставив (2.13.11) в (2.13.9), получим

(2.13.12)

Теплоемкость вещества зависит от температуры. Поэтому, чтобы вычислить интеграл, заменим функцию ее средним значением . В результате будем иметь:

(2.13.13)

Отсюда видно, что с повышением температуры энтропия растет по логарифмическому закону. Если при вычислении интеграла использовать саму функцию , а не ее среднее значение, то тенденция роста энтропии сохранится, но, естественно, не по логарифмическому закону.

Таким образом, вычисление энтропии, согласно (2.13.12), сводится к нахождению температурной зависимости теплоемкости.

5. Энтропия – мера беспорядка в системе.

Газ, находящийся при высокой температуре, имеет большую энтропию. При этом интенсивное движение молекул создает большую хаотичность в расположении молекул. При понижении температуры энтропия уменьшается, газ постепенно переходит в жидкое состояние, которое характеризуется более упорядоченным размещением молекул, уменьшается беспорядок в системе частиц. При дальнейшем уменьшении температуры энтропия еще более уменьшается, газ переходит в твердое состояние, отличительной чертой которого является высокая упорядоченность расположения частиц. При абсолютном нуле температуры хаотическое тепловое движение частиц прекращается, система становится полностью упорядоченной, а энтропия становится равной нулю. Таким образом, состояния с большим беспорядком характеризуется большой энтропией.

6. Энтропия системы определяется с точностью до произвольной постоянной (см.(2.13.9)).

7. Энтропия при переходе из одного состояния в другое не зависит от пути перехода, а определяется только начальным и конечным состоянием системы.

Это свойство энтропии следует из равенства Клаузиуса (2.13.7). В самом деле, пусть система обратимо переходит из состояния 1 в состояние 2 по нескольким различным путям (рис. 40).

Р и с. 40

Тогда из равенства Клаузиуса следуют равенства:

(2.13.14)

(2.13.15)

Из последних соотношений и равенства (2.13.10) следует утверждение седьмого свойства энтропии:

(2.13.16)

8. Количество теплоты, получаемое или отдаваемое при обратимом переходе из состояния 1 в состояние 2, определяется по формуле

(2.13.17)

Таким образом, в плоскости количество тепла численно равно площади под кривой процесса 12 (рис. 41)

Р и с. 41 Р и с. 42

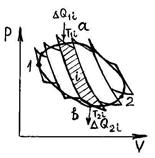
На рис. 42 в плоскости представлен обратимый цикл теплового двигателя. Количество теплоты получаемое за цикл рабочим веществом в процессе расширения равно площади фигуры т. е.

а количество теплоты, отдаваемое за цикл рабочим веществом,

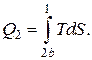
и, следовательно, определяется площадью фигуры 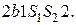Работа, произведенная рабочим веществом за цикл 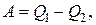равна площади, ограниченной замкнутой линией

Таким образом, плоскость примечательна тем, что в ней очень просто и наглядно представляются и количества теплоты, подводимой и отводимой в цикле, и работа, произведенная за цикл. К тому же, на плоскости легко видеть, на каких участках цикла подводится теплота, а на каких она отводится: участкам цикла, где рабочее вещество получает тепло, соответствует увеличение энтропии, а участкам цикла, где отдается тепло – уменьшение энтропии.

Представим цикл Карно в плоскости . Изотермам в плоскости будут соответствовать прямые 12 и 34, параллельные оси 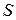, а адиабатам – прямые 23 и 41, параллельные оси T (рис. 43).

Р и с. 43

Количество теплоты, подводимое за цикл Карно, равно

(2.13.18)

а количество теплоты, отводимой за этот цикл,

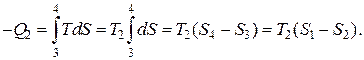
Откуда

(2.13.19)

Работа, произведенная рабочим веществом за цикл,

(2.13.20)

и, таким образом, определяется площадью прямоугольника 12341. Наконец, КПД цикла Карно

Используя для рассуждений плоскость , легко доказать третью теорему Карно.

Пусть имеется произвольный обратимый цикл. На рис. 44 площадь этого цикла заштрихована.

Р и с. 44

Найдем наибольшую 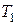и наименьшую 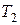температуры рабочего веще-ства в этом цикле. Согласно формулировке третьей теоремы Карно, тепловой двигатель, работающий по циклу 1234 Карно, имеет эти же температуры горячего и холодного источников.

По определению КДП произвольного обратимого цикла

(2.13.21)

а КПД обратимого цикла Карно

(2.13.22)

где – площади соответствующих областей, указанных на рис. 44. Из сравнения выражений (2.13.21–2.13.22) заключаем, что

(2.13.23)

Для произвольного необратимого цикла неравенство (2.13.23), очевидно, может только усилиться. Таким образом, третья теорема Карно доказана. Как видно из соотношений (2.13.21–2.13.22), КПД произвольного обрати-мого цикла тем выше, чем больше его площадь заполняет площадь прямоугольника 1234 цикла Карно.