Общее уравнение явлений переноса. Явления переноса. Общее уравнение явлений переноса в газах.

Равновесное состояние газа в молекулярно-кинетической теории рассматривается как состояние полной хаотичности движения молекул, распределение которых по скоростям подчиняется закону Максвелла. Любое неравновесное состояние газа всегда связано с нарушением полной хаотичности движения молекул и отклонениями от максвелловского распределения их по скоростям. Именно отклонениями от закона Максвелла объясняется направленный перенос энергии, импульса и массы в газах. В каждом конкретном случае внешнего воздействия на газ, выведшего его из равновесия, необходимо найти распределение, заменяющее максвелловское, и лишь затем можно перейти к изучению закономерностей явлений переноса, вызываемого этим воздействием. Этот строгий путь исследования явлений переноса приводит к значительным математическим трудностям, которые до конца не преодолены до сих пор. Поэтому мы рассмотрим только основные закономерности явлений переноса и их приближенное качественное обоснование.

Ввиду хаотичности теплового движения молекул приближенно можно считать, что молекулы движутся только вдоль трех взаимно перпендикулярных осей. При этом вдоль каждой оси движется 1/3 всех молекул газа. Движение молекул вдоль каждой оси в обоих направлениях равновероятно. Поэтому в положительном направлении каждой из осей движется 1/6 часть общего числа молекул. Будем также считать, что все молекулы имеют одну и ту же скорость, равную их средней скорости .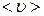

Выберем площадку dS, расположенную перпендикулярно оси X. Тогда число частиц, проходящих через эту площадку за время dt

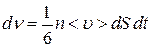, (4.4.1)

где n – число частиц в единице объема.

В явлениях переноса каждая молекула при своем хаотическом движении переносит некоторую физическую величину. В случае теплопроводности переносимой величиной является кинетическая энергия молекулы, которая переносится оттуда, где она больше (выше температура), туда, где она меньше (ниже температура), в случае вязкого трения молекула переносит импульс, т. е. величину, равную произведению массы молекулы на гидродинамическую скорость направленного движения слоя газа или жидкости, и, наконец, в явлении диффузии переносимой величиной служит концентрация диффундирующей компоненты, рассчитанная на одну молекулу.

Будем считать, что переносимая величина 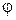, отнесенная к одной молекуле, изменяется только в направлении оси X. Значение этой величины изменяется при столкновениях молекул и сохраняется постоянной между соударениями, т. е. на длине свободного пробега 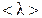. Расположим площадку dS, перпендикулярно оси X, в точке x (рис. 60).

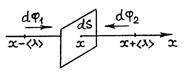
Р и с. 60

Молекулы, пересекающие выделенную площадку слева направо, переносят через нее то значение величины 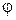, которое они имели после последнего столкновения перед площадкой, т. е. 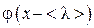. Поток этой величины, согласно (4.4.1)

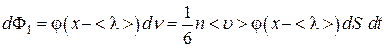. (4.4.2)

Аналогично, поток величины 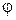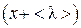справа налево

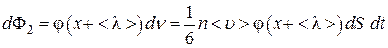. (4.4.3)

Результирующий поток в направлении оси X

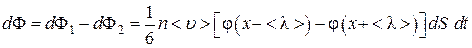. (4.4.4)

Если бы переносимая величина 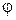была постоянна по всему объему, занимаемому газом (равновесие), то потоки этой величины через площадку 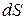слева направо и справа налево были бы одинаковы, и результирующий поток был бы равен нулю. Поэтому, чтобы выявить сущность явлений переноса, берется разность соответствующих потоков, которая определяет поток 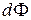в направлении оси X.

Разложим функции 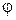, стоящие в квадратной скобке выражения (4.4.4), в ряд по степеням малой величины 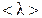в точке x:

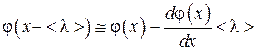, (4.4.5)

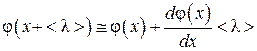. (4.4.6)

Подставим разложения (4.4.5–4.4.6) в (4.4.4). В результате будем иметь

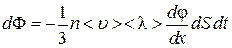. (4.4.7)

Соотношение (4.4.7) является общим уравнением переноса физической величины 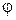и имеет такой же вид, как и в строгой теории, кроме множителя 1/3, который в строгой теории имеет значение близкое к 1/3.

60. Теплопроводность. Уравнение теплопроводности. Основной закон теплопроводности – закон Фурье. Вычисление и экспериментальное определение коэффициента теплопроводности.

Явление теплопроводности наблюдается всегда, если в веществе имеется разность температур, обусловленная какими-либо внешними причинами. С макроскопической точки зрения явление теплопроводности заключается в переносе тепла от горячего слоя к холодному и продолжающемуся до тех пор, пока температура во всем теле не выровняется. В молекулярно-кинетической же теории процесс теплопроводности объясняется тем, что молекулы из горячего слоя, где они имеют большую среднюю кинетическую энергию, проникая в холодную область, передают при столкновениях молекулам этой области часть их кинетической энергии.

Пусть изменение температуры вещества происходит вдоль оси X, в то время как в плоскости, перпендикулярной этой оси, температура постоянна. Опытным путем Ж. Фурье установил закон, согласно которому количество тепла, переносимое за время dt через площадку dS, перпендикулярную оси X, пропорционально величине площадки, времени переноса и градиенту dT/dx температуры:

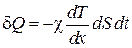, (4.5.1)

где 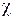– коэффициент теплопроводности, который, как видно из закона Ж. Фурье, имеет в системе СИ размерность Дж/(м∙с∙K) = Вт/(м∙K), и численно равен количеству тепла, переносимого в единицу времени через единичную площадку при градиенте температуры, равном единице. Знак “минус” означает, что тепло переносится от мест более горячих к более холодным.

Закон Ж. Фурье справедлив для веществ, находящихся в любых агрегатных состояниях.

Введем в рассмотрение плотность потока тепла

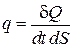, (4.5.2)

т. е. величина q равна количеству тепла, проходимого через единичную площадку в единицу времени. С учетом (4.5.2) закон Фурье примет вид

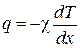. (4.5.3)

Если нагреть некоторую часть тела, то начнется необратимый процесс теплопроводности. При этом, если зафиксировать координату x в теле, то температура в этой точке будет, очевидно, изменяться со временем, достигая, в конце концов, равновесной температуры. Поэтому температура T является не только функцией координаты x, но и времени t, т. е. T = T(x, t). Тогда, как видно из (4.5.3), поток q будет зависеть от x и t, т. е. q = q(x, t). Процесс теплопроводности, при котором температура и поток являются функциями времени, называется нестационарным.

Выделим в теле, где происходит одномерный (вдоль оси X) нестационарный процесс теплопроводности, элементарный параллелепипед с площадью основания dS и высотой dx (рис. 61).

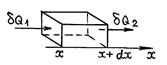
Р и с. 61

Количество тепла, входящее в параллелепипед за время dt через основание с координатой x,

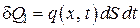, (4.5.4)

а уходящее через основание с координатой x+dx за то же время

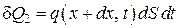. (4.5.5)

Такимобразом, тепло, поступившее в параллелепипед за время dt,

. (4.5.6)

С другой стороны это тепло можно выразить через теплоемкость тела:

, (4.5.7)

где dm и dT – масса и приращение температуры вещества, заключенного в параллелепипеде, соответственно; 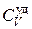и – удельная теплоемкость и плотность вещества.

Разложим функцию q(x+dx, t) в ряд по степеням dx в точке x:

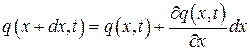. (4.5.8)

Из выражений (4.5.6–4.5.8) находим

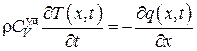. (4.5.9)

Подставляя в последнее уравнение вместо q(x, t) его выражение (4.5.3), получим

. (4.5.10)

Если коэффициент теплопроводности не зависит от x (однородное вещество), то уравнение (4.5.10) примет вид:

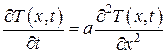. (4.5.11)

где 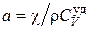– коэффициент температуропроводности.

Уравнения (4.5.10–4.5.11) носят название дифференциальных уравнений теплопроводности Ж. Фурье. Искомой функцией в этих уравнениях является распределение температуры T(x, t) по пространству и во времени.

Коэффициент температуропроводности a является физическим параметром вещества и имеет размерность 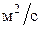. В нестационарных тепловых процессах коэффициент a характеризует скорость изменения температуры. Если коэффициент теплопроводности 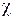характеризует способность вещества проводить теплоту, то коэффициент температуропроводности a есть мера теплоинерционных свойств вещества. В самом деле, из уравнения (4.5.11) следует, что изменение температуры в единицу времени 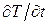для любой точки вещества пропорционально величине a. Поэтому при прочих одинаковых условиях быстрее увеличивается температура у того вещества, которое имеет больший коэффициент температуропроводности. Сама же величина a тем больше, чем больше тепла способно пропустить вещество в единицу времени через единичную площадку при единичном градиенте температуры (т. е. чем больше 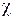) и чем меньше плотность и теплоемкость вещества. Из опыта известно (см. табл. 4.5.1), что газы имеют малый, а металлы большой коэффициент температуропроводности. Однако для тех и других веществ он является весьма малой величиной, что свидетельствует о медленности процесса теплопроводности.

Таблица 4.5.1