Теплопроводность и вязкое трение в ультраразреженных газах.

Так как в сильно разреженных газах молекулы движутся без соударений, то механизм теплообмена и трения носит существенно иной характер по сравнению с плотными газами. В разреженных газах нельзя выделить слои и рассматривать передачу энергии или импульса соударяющимися молекулами от слоя к слою, как мы это делали в плотных газах.

Рассмотрим процессы теплообмена и трения на основе следующей модели механизма этих процессов в разреженных газах. Пусть в газ погружены две твердые пластинки, расстояние между которыми равно h. Молекула газа, столкнувшись с пластинкой, на очень небольшое время оседает на ней, затем покидает ее, получив энергию, соответствующую температуре этой пластинки. (В действительности взаимодействие молекул с пластинкой имеет более сложный характер.)

Как мы знаем, при теплообмене молекулы переносят кинетическую энергию от мест более горячих к местам более холодным. Обозначим температуры пластинок через T₁ и T₂ (T₁ >T₂). В нашей модели молекула, отлетевшая от горячей пластинки, имеет в среднем кинетическую энергию <E_k1>, соответствующую температуре T₁ этой пластинки. Столкнувшись потом с холодной пластинкой, она отлетает от нее с энергией <E_k2>, соответствующей температуре T₂ холодной пластинки. В результате энергия, переданная молекулой от горячей к холодной пластинке, равна <E_k1> – <E_k2>. Точно так же, молекула, отскочившая от холодной пластинки с энергией <E_k2>, после столкновения с горячей пластинкой отскочит от нее с энергией <E_k1>, и далее, столкнувшись с холодной пластинкой, будет иметь энергию <E_k2>. В результате горячая пластинка отдает холодной ту же энергию <E_k1> – <E_k2>. Таким образом, каждая молекула после ряда столкновений переносит энергию от горячей к холодной пластинке, равную <E_k1> – <E_k2>. Количество же энергии (тепловой), переносимое dν молекулами за время dt от более горячей площадки dS к более холодной такой же площадке, будет равно

.(4.9.15)

Учитывая формулы (1.4.12) и (4.6.2), последнее выражение можно представить в виде:

,(4.9.16)

где 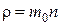– плотность газа.

Хотя понятие о градиенте температуры в разреженном газе лишено смысла, мы формально в законе Фурье вместо dT/dx подставим величину (T₂–T₁)/h:

.(4.9.17)

Сравнивая (4.9.16) и (4.9.17), получим выражение для коэффициента теплопередачи в вакууме:

,(4.9.18)

где учтено, что для идеального газа . Из последней формулы видно, что с уменьшением давления падает и теплопередача разреженного газа. Теплопроводность же плотных газов, как мы знаем, от давления не зависит.

Рассмотрим теперь явление трения, которое испытывают тела в разреженных газах. Пусть в газе параллельно друг другу в одном направлении (оси Х) движутся две пластинки, которые находятся при одной и той же температуре, равной температуре газа.

Если бы пластинка покоилась относительно начала оси Х, то произвольная молекула, двигающаяся со средним тепловым импульсом m₀<υ> отразилась бы от пластинки, имея тот же тепловой импульс m₀<υ>. Однако пластинка движется, поэтому молекула отразится от нее, имея дополнительную составляющую (вдоль оси X) m₀u₁ импульса, соответствующую скорости пластинки. Столкнув­шись потом с другой пластинкой, имеющей скорость u₂, молекула отразится с дополнительным импульсом m₀u₂.

Таким образом, после столкновения с пластинками импульс каждой молекулы изменяется на величину m₀(u₁ – u₂). Изменение же импульса dν молекул, ударяющихся о площадку dS пластинки за время dt, согласно формуле (1.4.12), равно

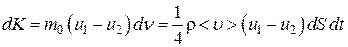.(4.9.19)

Чтобы определить коэффициент трения в разреженном газе, в законе Ньютона (4.7.6) для вязкого трения формально заменим du/dx на

(u₂ – u₁)/h, где h – расстояние между пластинками. В результате будем иметь

.(4.9.20)

Сравнивая (4.9.19) и (4.9.20), получим

.(4.9.21)

Из последней формулы видно, что коэффициент трения уменьшается с уменьшением давления разреженного газа, тогда как для плотных газов он от давления не зависит.

Из выражения (4.9.19) следует, что сила, действующая на единицу площади пластинки

.(4.9.22)