Кипение. Перегрев жидкостей.

Кипение – процесс интенсивного парообразования жидкости, включающий рождение пузырьков пара, их рост и движение к поверхности жидкости. Кипение, характеризующееся образованием пузырьков пара на поверхности соприкосновения жидкости с твердым телом, называется поверхностным. В реальных условиях мы всегда имеем дело с поверхностным кипением, которое происходит на границе между жидкостью и твердым телом, нагретым выше температуры кипения (нагреватель). При нагревании жидкости до начала кипения основная часть подводимой теплоты расходуется на нагревание, остальная – на испарение. Пусть температура дна сосуда T₁, температура жидкости на свободной поверхности T₂. До тех пор, пока температурный перепад 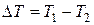невелик, теплота переносится в жидкой среде только путем теплопроводности. В этом случае, как мы знаем, стационарное распределение температуры в жидкости удовлетворяет одномерному уравнению теплопроводности (4.5.21). Решением этого уравнения является функция (4.5.23), т. е. температура жидкости падает линейно от дна сосуда (x = 0) до свободной поверхности (x = d). При этом градиент температуры постоянен и равен (рис. 78, а).

а б в

Р и с. 78

При дальнейшем повышении температуры дна сосуда T₁ растет и температурный градиент в жидкой среде. Когда последний достигнет определенной величины, возникает свободная конвекция, и теплота в жидкости начинает переноситься интенсивнее (свободная конвекция тепла возникает под действием архимедовых сил и заключается в переносе верти­кально вверх масс более нагретой жидкости и опускании на ее место менее нагретой). Теперь стационарное распределение температуры определяется известным уравнением конвективного теплообмена

, (5.7.1)

где – скорость жидкости при конвекции, a – коэффициент темпера-туропроводности. Считая скорость жидкости в первом приближении постоянной, приходим к экспоненциальному убыванию температуры с высотой (рис. 78, б). Это приводит к значительному увеличению градиента температуры в жидкости на границе с горячим дном, и, таким образом, увеличивается теплоотдача к жидкости. Пусть, наконец, температура дна стала столь значительной, что на его поверхности начинают возникать паровые пузырьки, которые постепенно увеличиваются, отрываются и всплывают. В жидкости устанавливается процесс кипения. Как показывают опыты, теплообмен в этом случае становится еще более интенсивным. Вследствие этого падение температуры жидкости вблизи горячей твердой поверхности будет происходить еще круче, чем при конвекции (рис. 78, в).

Процесс поверхностного кипения начинается на дне сосуда, граничащего с нагревателем. В порах дна сосуда всегда имеется воздух или другой растворенный газ, который является генератором будущих пузырьков пара. По мере испарения жидкости внутрь пузырьков, давление пара в них повышается, пузырек начинает расти. Уве­личение размеров пузырька происходит особенно быстро, когда при некоторой температуре T_S давление p(T_S) насыщенного пара в нем становится равным или немного больше внешнего давления, т. е. p(T_S) = p_внеш. Тогда пузырек отрывается от дна и под действием архимедовой силы поднимается к поверхности жидкости.

Внешнее давление p_внеш слагается из атмосферного давления p₀, гидростатического давления (ρ– плотность жидкости, h – глубина, на которой образуется пузырек) и давления Лапласа (R – радиус пузырька, 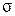– коэффициент поверхностного натяжения жидкости). Таким образом, процесс кипения начнется при условии, что давление насыщенных паров при данной температуре T_S

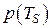/ . (5.7.2)

Температуру T_S жидкости, при которой давление p(T_S) ее насыщенного пара становится равным внешнему давлению p_внеш на жидкость, называют температурой кипения этой жидкости. Из равенства

(5.7.3)

следует, что температура кипения является функцией внешнего давления. Поэтому сказать, что температура кипения данного вещества равна T_S, без указания, при каком внешнем давлении она получена, некорректно.

Мы знаем, что давление насыщенного пара жидкости уменьшается при понижении температуры и увеличивается при ее повышении, следовательно, и температура кипения жидкости понижается при уменьшении внешнего давления и повышается при его увеличении. Таким образом, если некоторая функция выражает зависимость давления насыщенных паров от температуры, то функция, обратная ей, определяет зависимость температуры кипения от внешнего давления. Так как уравнение Клапейрона-Клаузиса

в дифференциальной форме выражает зависимость давления насыщенных паров от температуры, то уравнение

(5.7.4)

определяет в дифференциальной форме зависимость температуры кипе-

ния от внешнего давления, т. е. уравнение (5.7.4) является уравнением кривой кипения в дифференциальной форме. В этом уравнении dT – изменение температуры кипения жидкости при изменении внешнего давления на dp.

В заключение отметим: если продолжительным кипячением из жидкости удалить воздух или другой растворенный газ, то эту жидкость можно нагреть до температуры, значительно большей, чем температура ее кипения при данном внешнем давлении. Так, полученную жидкость называют перегретой. Если в перегретую жидкость внести неоднородности, к примеру, забросить в нее песчинки, в порах которых находится воздух, то жидкость бурно вскипает, напоминая взрыв.

?73. Аморфное и кристаллическое состояние вещества. Симметрия твердых тел. Основные элементы симметрии твердых тел.

В физике различают аморфные и кристаллические твердые тела. По признаку сохранения формы аморфные тела относят к твердым, во всем остальном они не отличаются от жидкостей. Аморфные тела рассматривают как переохлажденные жидкости с аномально большим коэффициентом вязкости, благодаря которому они при обычной температуре не могут течь. Однако при повышении температуры они постепенно размягчаются, не имея определенной температуры плавления, и приобретают обычную для жидкостей способность течь. Свойства аморфных тел одинаковы по всем направлениям, т. е. они изотропны. К примеру, если из стекла (аморфное тело) изготовить шар, то его свойства окажутся одинаковыми в различных направлениях. Так, при сжатии его с одинаковой силой в разных направлениях, он будет уменьшаться на одинаковую величину. Если измерять теплопроводность стекла, нагревая шар сверху и охлаждая его снизу или нагревая слева и охлаждая справа, найдем, что теплопроводность стекла во всех направлениях также одинакова. Для лучей света, пронизывающих стекло по всем направлениям, показатель преломления также оказывается одинаковым. Если поместить стеклянный шар между двумя пластинами заряженного конденсатора и вращать шар вокруг его центра, то не будет отмечено никакого изменения емкости конденсатора; это значит, что диэлектрическая постоянная не зависит от направления электрического поля внутри его.

Совершенно иначе ведут себя кристаллические твердые тела. Кристаллы имеют определенную, зависящую от внешнего давления температуру плавления. Скорость распространения света, изотермический коэффициент сжатия, коэффициент теплопроводности, модуль упругости, диэлектрическая проницаемость и многие другие физические свойства кристалла сильно зависят от направления в нем.

Кристаллы можно получать различными способами, например, охлаждением жидкости. При таком охлаждении, если не принять специальных мер, в жидкой фазе возникает множество центров кристаллизации, вокруг которых происходит образование твердой фазы. Возникает множество мелких кристалликов, сливающихся друг с другом хаотически и образующих так называемый поликристалл. Хотя каждый из кристаллов, образующих поликристалл, анизотропен, но ввиду хаотичности ориентировки этих кристаллов поликристаллическое тело в целом является изотропным.

Если же в охлажденную жидкость ввести затравку – маленький кристаллик, то кристаллизация начнется на нем, и можно вырастить большой монокристалл правильной формы. Для этого необходимо, чтобы условия роста кристалла были одинаковы на всех его поверхностях, что может быть достигнуто вращением затравки в растворе. При выращивании больших монокристаллов металлов и полупроводников затравку очень медленно со скоростью несколько миллиметров в час выдвигают в вертикальном направлении из нагревательной печи.

Согласно закону, открытому в 1783 г. Роме де Лиллем, во всех кристаллах одного и того же вещества углы между соответственными гранями равны. Так, например, в кристаллах каменной соли (NaCl) все углы между гранями 90˚. Если из такого кристалла выточить шарик и поместить его в насыщенный раствор каменной соли, то кубическая форма кристалла будет стремиться восстановиться. Причиной такого восстановления формы кристаллов является хорошо известное условие устойчивости равновесия термодинамической системы: условие минимума потенциальной энергии. Для кристаллов это условие выражено в принципе, сформулированном Гиббсом, Кюри и Вульфом: поверхностная энергия должна быть минимальной. Этот минимум должен находиться при условии, что заданы углы между гранями кристалла.

При помещении кристалла в насыщенный раствор или в расплав между твердой и жидкой фазами устанавливается динамическое равновесие: атомы из твердой фазы переходят в жидкую фазу, а из жидкой – в твердую; но осаждение из жидкой фазы идет так, что образуется система с минимумом потенциальной энергии, т. е. образуется характерная для данного вещества форма кристалла и все бывшие нарушения этой формы исчезают, потому шарик в описанном опыте стремится превратиться вновь в кубическую структуру или другую характерную кристаллическую форму.

Если условия роста кристалла неодинаковы в разных точках его поверхности, то форма растущего кристалла может быть отлична от характерной формы, хотя углы между основными гранями остаются та­кими, как и при правильной форме.