Теплоемкость твердых тел. Классическая теория и ее недостатки.

Мы знаем, что вещество находится в твердом состоянии, если энергия kT тепловых движений значительно меньше минимальной потенциальной энергии 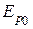взаимодействия частиц между собой. Атомы в кристалле совершают колебания около положений равновесия. При подводе тепла к нему амплитуда и энергия этих колебаний растут. При небольших амплитудах колебания можно считать гармоническими. Полная энергия E колебаний частицы равна сумме кинетической E_k и потенциальной E_p энергий, т. е. E = E_k + E_p. Средние значения этих энергий за период одного колебания одинаковы <E_k> = <E_p>, поэтому E = 2 <E_k>, тогда как для идеального газа E = <E_k>.

Согласно теореме о равномерном распределении энергии, независимо от химической природы и массы частицы на каждую ее степень свободы приходится кинетическая энергия kT/2, а полная энергия E = kT. Так как каждая частица кристалла обладает тремя степенями свободы, то энергия ее в среднем равна 3kT. Если кристалл содержит N атомов, то его внутренняя энергия

, (6.7.1)

где ν – число молей кристалла. Используя формулу (2.5.12) и (6.7.1), найдем молярную теплоемкость при постоянном объеме атом­ного кристалла:

. (6.7.2)

Это точно в два раза больше молярной теплоемкости при постоянном объеме идеального одноатомного газа (см. формулу (2.5.16)). Поэтому перевод одноатомного газа в твердое состояние удваивает его молярную теплоемкость при постоянном объеме.

Из формулы (6.7.2) следует, что молярная теплоемкость атомных кристаллов есть величина постоянная, независимая от природы атомов и температуры. Это утверждение носит название закона Дюлонга и Пти.

Как было показано Нейманом и Коппом, молярные теплоемкости молекулярных кристаллов равны суммам атомных теплоемкостей содержа­щихся в них атомов:

, (6.7.3)

где m – общее число атомов в химической формуле молекулы.

Опыт показывает, что при температурах, близких к комнатным, теплоемкость большинства кристаллов действительно близка к величине 3R∙m (табл. 6.7.1). Имеются все же исключения: теплоемкости алмаза, бериллия, кремния и бора значительно меньше, чем 3R и при комнатных температурах.

Таблица 6.7.1

Вещество	Cu	Ag	Pb	NaCl	AgCl	CuCl2	PbCl2
	23,6	24,0	24,7	51,4	54,7	77,7	77,3

Однако при высоких и особенно при низких температурах наблюдаются значительные отступления от закона Дюлонга и Пти и его обобщения, данного Нейманом и Коппом. Отклонения от указанных законов свидетельствуют о нарушении классического принципа равномерного распределения энергии по степеням свободы. Это нарушение обусловлено квантовой природой колебаний атомов (осцилляторов) в кристалле. Согласноквантовой механике, колеблющиеся атомы кристалла могут получать энергию только дискретными порциями:

. (6.7.4)

Собственная частота колебаний атомов в кристалле . Поэтому энергия первого уровня . При температуре

T = 300k средняя тепловая энергия kT = 4,1∙10^-21Дж сравнима по порядку величины с энергией кванта осциллятора. Поэтому можно сказать, что при температурах, близких к комнатным, почти все атомы кристалла будут возбуждены энергией E₁ и насыщены тепловой энергией в соответствии с теоремой о равномерном распределении.

При низких температурах средняя тепловая энергия kT настолько мала (kT < hν), что ее недостаточно для возбуждения тепловых колебаний атомов кристалла. Большинство из них будет находиться на так называемом нулевом энергетическом уровне и совершать нулевые (сохраняющиеся при абсолютном нуле температуры) нетепловые колебания. Термически же будет возбуждена лишь небольшая часть атомных осцилляторов. В результате средняя энергия осциллятора будет меньше kT. Поэтому при низких температурах теплоемкость квантовых осцилляторов должна быть меньше теплоемкости классических осцилляторов.

Найдем зависимость теплоемкости от температуры для атомных кристаллов.

Тепловая энергия, переданная кристаллу, случайным образом распределяется между атомами (осцилляторами). Вычислим среднее значение энергии, которую может получить осциллятор. По определению среднего

, (6.7.5)

где P_n – вероятность того, что n-й атом приобретает энергию E_n. Эта вероятность, как мы знаем, определяется по формуле Больцмана:

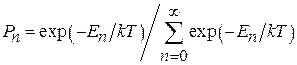. (6.7.6)

Подставим распределение Больцмана (6.7.6) в выражение (6.7.5) и учтем, что :

, (6.7.7)

где введено обозначение . Знаменатель в последнем соотношении представляет геометрическую прогрессию, сумма которой

. (6.7.8)

Сумма ряда, стоящего в числителе выражения (6.7.7) вычисляется следующим образом:

. (6.7.9)

Подставляя (6.7.8) и (6.7.9) в (6.7.7), получим

. (6.7.10)

Если твердое тело находится при температуре T, то выражение (6.7.10) определяет среднюю энергию колебаний атома, приходящуюся на одну его степень свободы. При высоких температурах, когда <<1, exp ( ) и выражение (6.7.10) приобретает вид:

, (6.7.11)

что совпадает со значением в классической теории. При низких температурах в знаменателе (6.7.10) можно пренебречь единицей, тогда получим

. (6.7.12)

Отсюда видно, что при низких температурах энергия квантового осциллятора спадает по экспоненциальному закону и асимптотически стремится к нулю при T .

При произвольном направлении колебаний относительно выбранной системы координат, атом имеет три степени свободы и его энергия колебаний равна 3 , а энергия ν₀ молей – . Эта величина определяет внутреннюю энергию ν₀ молей твердого тела, находящегося при температуре T, т. е.

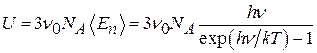. (6.7.13)

Используя формулу (2.5.12) для вычисления молярной теплоемкости при постоянном объеме, получим

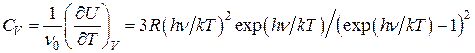. (6.7.14)

При высоких температурах <<1 и exp( ) . Поэтому

,

При высоких температурах из выражения (6.7.14) следует закон Дюлонга и Пти. При низких температурах ( >>1) из формулы (6.7.14) следует, что теплоемкость

, (6.7.15)

и при T , С_V . Однако из опыта следует, что при низких
температурах теплоемкость С_V стремится к нулю не по экспоненциальному закону (6.7.15), а пропорционально T³. Поэтому формула Эйнштейна (6.7.14) является приближенной, что хорошо видно из рис. 95, где приведены экспериментальная кривая 1 зависимости теплоемкости серебра от температуры и кривая 2, вычисленная по формуле (6.7.14).

Переход от высокотемпературной области, где выполняется
класссический закон, к низкотемпературной области, где проявляется
квантовая природа атомных осцилляторов, определяется равенством
тепловой энергии kT и энергии кванта осциллятора hν. Отсюда находим характеристическую температуру 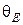по Эйнштейну:

. (6.7.16)

В таблице 6.7.2 приведены значения для некоторых веществ.

Таблица 6.7.2

Вещество	Алмаз	Be	CaF2	Fe	W	Zn	Ag	Hg
; k

Как видно из таблицы 6.7.2, характеристическая температура Эйнштейна для алмаза и бериллия находится значительно выше обычных температур, т. е. комнатная температура для этих веществ должна считаться низкой, когда для вычисления теплоемкости следует пользоваться формулой Эйнштейна (6.7.14), а не законом Дюлонга – Пти (6.7.2).

Р и с. 95