Классические методы оптимизации в математике, их применение в экономике

Задачей оптимизации называется задача о поиске экстремума функции или функционала на заданном множестве допустимых решений.

Весь материал сборника разбит на две части: «Оптимизация в условиях полной определенности» и «Принятие решений в условиях неопределенности и риска», традиционно выделяемые при преподавании курса «Количественные методы в менеджменте» и содержащие следующие разделы:

● Оптимизация в условиях полной определенности

○ Метод линейной оптимизации

○ Транспортные задачи и логистика; задачи о назначениях и отборе

○ Планирование и анализ проектов

○ Оптимальное управление запасами

○ Комплексное и многопериодное планирование

● Принятие решений в условиях неопределенности и риска

○ Оптимальное управление запасами с учетом случайных вариаций спроса

○ Выбор альтернатив

○ Управление проектами с учетом случайных вариаций времени выполнения

○ Оценка эффективности систем массового обслуживания и их оптимизация

Задачей оптимизации в математике, информатике и исследовании операций называется задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.

Математическое программирование — дисциплина, изучающая теорию и методы решения задачи оптимизации.

В процессе проектирования ставится обычно задача определения наилучших, в некотором смысле, структуры или значений параметров объектов. Такая задача называется оптимизационной. Если оптимизация связана с расчетом оптимальных значений параметров при заданной структуре объекта, то она называется параметрической оптимизацией. Задача выбора оптимальной структуры является структурной оптимизацией.

Стандартная математическая задача оптимизации формулируется таким образом. Среди элементов χ, образующих множества Χ, найти такой элемент χ* , который доставляет минимальное значение f(χ*) заданной функции f(χ). Для того, чтобы корректно поставить задачу оптимизации необходимо задать:

● Допустимое множество — множество ;

● Целевую функцию — отображение ;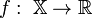

● Критерий поиска (max или min).

Тогда решить задачу означает одно из:

● Показать, что .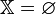

● Показать, что целевая функция не ограничена снизу.

● Найти .

● Если , то найти .

Если минимизируемая функция не является выпуклой, то часто ограничиваются поиском локальных минимумов и максимумов: точек таких, что всюду в некоторой их окрестности для минимума и для максимума.

Если допустимое множество , то такая задача называется задачей безусловной оптимизации, в противном случае — задачей условной оптимизации.

Общая запись задач оптимизации задаёт большое разнообразие их классов. От класса задачи зависит подбор метода (эффективность её решения). Классификацию задач определяют: целевая функция и допустимая область (задаётся системой неравенств и равенств или более сложным алгоритмом)[1].

Методы оптимизации классифицируют в соответствии с задачами оптимизации:

● Локальные методы: сходятся к какому-нибудь локальному экстремуму целевой функции. В случае унимодальной целевой функции, этот экстремум единственен, и будет глобальным максимумом/минимумом.

● Глобальные методы: имеют дело с многоэкстремальными целевыми функциями. При глобальном поиске основной задачей является выявление тенденций глобального поведения целевой функции.

Существующие в настоящее время методы поиска можно разбить на три большие группы:

● детерминированные;

● случайные (стохастические);

● комбинированные.

● 107 Понятие государственного бюджета. Дефицит и профицит бюджета

● Государственный бюджет (от англ. budget — сумка, кошелек) — это смета доходов и расходов госу дарства на определенный период времени, составленная с указанием источников поступления государст венных доходов и направлений, каналов расходования денег.

● Государственный бюджет составляется правительством и утверждается высшими законодательными органа ми (в России – в виде закона Государственной Думы Федерального Собрания РФ). По окончании финансового года Правительство Российской Федерации должно отчитаться об исполнении бюджета.

● Доходы государственного бюджета:

● Налоги на доходы юридических и физических лиц

● Поступления от реального сектора (налог на прибыль)

● Поступление косвенных налогов и акцизов

● Пошлины и неналоговые сборы

● Региональные и местные налоги

● Расходы государственного бюджета:

● Промышленность

● Социальная политика

● Сельское хозяйство

● Государственного управление

● Международная деятельность

● Оборона

● Правоохранительная деятельность

● Наука

● Здравоохранение

● Сбалансированный бюджет — бюджет, в котором равны соотношения доходов и расходов.

● В случае если доходы и расходы в бюджете разняться то дефицит или профицит бюджета.

● Бюджетный дефицит — это сумма, на которую расходы государства превышают его доходы.

● Бюджетный профицит — это сумма, на которую доходы государства превышают его расходы. Профицит возникает достаточно редко, чаще всего наблюдается дефицит бюджета. То есть для осуществления всех расходов необходимо найти дополнительные средства. Эти средства поступают из источников финансирования бюджетного дефицита.

● Источники финансирования бюджетного дефицита

● Внутренее финансирование:

● выпуск и продажа ценных бумаг (облигации и векселя)

● бюджетные ссуды, полученные от бюджетов других уровней

● использование средств центрального банка

● Внешнее финансирование:

● продажа ценных бумаг на мировом финансовом рынке

● кредиты иностранных банков и междунароных финансовых организаций

● кредиты иностранных правительств

● Вместе внутренее и внешнее финансирование составляют общий объем финансирования.