
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Средние величины, их значение в статистике, виды и области научного применения.
Средней величиной в статистике называется обобщающая характеристика совокупности однотипных явлений по какому-либо количественно варьирующему признаку, отражающая уровень этого признака в расчете на единицу совокупности.
Вычисление среднего уровня – наиболее распространенный прием обобщения. Средний показатель одним числом описывает совокупность в целом. Он отражает то общее, что характерно (типично) для всех единиц совокупности и погашает индивидуальные различия величин, вызванные влиянием случайных факторов. В соответствии со свойством средней арифметической величины, сумма отклонений индивидуальных вариантов от средней арифметической величины равна нулю:
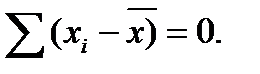
Основным условием достоверности средних величин является однородность изучаемой совокупности. Нарушение этого требования приводит к появлению фиктивных (ненадежных, нетипичных) средних. Поэтому метод средних надо использовать в сочетании с методом группировок.
В ряде случаев статистика использует так называемые системные средние величины, обобщающие неоднородные явления, например: средний доход на душу населения, средняя заработная плата занятых в экономике и т.п., – все эти средние показатели используются в сравнительном анализе у разных объектов (стран) и в динамике.
Средние величины делятся на два класса: математические (степенные) и структурные. К математическим относятся средняя арифметическая, средняя квадратическая, средняя геометрическая, средняя гармоническая величины. К структурным средним относятся мода и медиана и др. показатели структуры вариационного ряда.
Математические средние выводятся из формулы степенной средней величины:

где xi –варианты;
n – число вариантов;
m – показатель степени средней.
Значение показателя степени средней определяет вид средней величины.
При m = 1, получается средняя арифметическая:
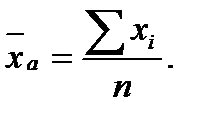
При m = 2 получается средняя квадратическая:

Применяется при расчете показателей вариации (среднее квадратическое отклонение).
При m = 0 получается средняя геометрическая:

Применяется при расчете показателей динамики (средний темп роста).
При m = - 1 получается средняя гармоническая:
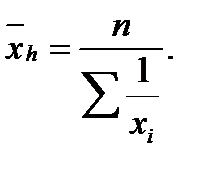
Средняя гармоническая считается преобразованной формой средней арифметической. Средняя арифметическая и средняя гармоническая взвешенные величины являются тождествами.
Структурные средние мода и медиана применяются для изучения внутреннего строения вариационных рядов. Они не являются обобщающим характеристиками совокупности, т.к. соответствуют определенным значениям признака.
Мода– это наиболее типичное, чаще всего встречаемое значение признака в данной совокупности, т.е. вариант с наибольшей частотой.
Медиана– это вариант, который находится в середине упорядоченной (ранжированной) совокупности. По обе стороны от медианы находится одинаковое число единиц совокупности. Медиана показывает значение признака, достигнутое половиной единиц изучаемой совокупности.
Стадийность в проектировании, состав проектных материалов каждой стадии. Нормативные документы о проектировании. Виды мелиоративных систем в зависимости от их назначения, состав объектов, входящих в мелиоративную систему.
Дата добавления: 2015-04-18; просмотров: 341; Мы поможем в написании вашей работы!; Нарушение авторских прав |