С отрицательной обратной связью по напряжению

Вырожденная структурная схема СУЭП (рис. 3.5) с отрицательной обратной связью по напряжению получается из исходной структурной схемы (рис. 3.4) при p=0 и применятся для анализа статических режимов работы СУЭП.

Из структурной схемы (рис. 3.5) видно, что управляющим (задающим) воздействием является напряжение задания Uз на входе регулятора. Возмущающим воздействием является статический ток Iс, прикладываемый в двух точках системы регулирования к сумматорам Σ2 и Σ3.

Рис.3.5. Вырожденная структурная схема СУЭП с отрицательной обратной связью по напряжению

Если возмущающее воздействие приравнять нулю, то получим структурную схему (рис. 3.6,а), в которой входной величиной является напряжение задания Uз, а выходной – скорость идеального холостого хода ω0зам. Свернув звенья, охваченные отрицательной обратной связью (рис. 3.6,б) и выполнив окончательные преобразования, получим структурную схему, представленную на рис. 3.6,в, из которой можно получить передаточный коэффициент системы регулирования по управляющему воздействию:

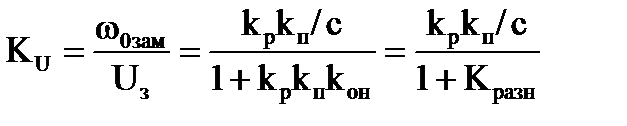(3.5)

где 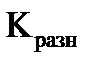- коэффициент разомкнутой системы с обратной связью по напряжению.

Из (3.5) можно определить скорость идеального холостого хода в замкнутой системе регулирования:

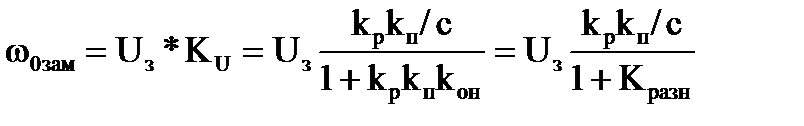(3.6).

Рис. 3.6. Преобразования структурной схемы по управляющему воздействию

Если теперь приравнять нулю управляющее воздействие (Uз=0), то получим структурную схему относительно возмущающего воздействия по второму сумматору (рис. 3.7,а) и третьему сумматору (рис. 3.7,г). Поэтому коэффициент передачи по возмущающему воздействию складывается из двух составляющих в соответствии с рис. 3.7, в и 3.7, д:

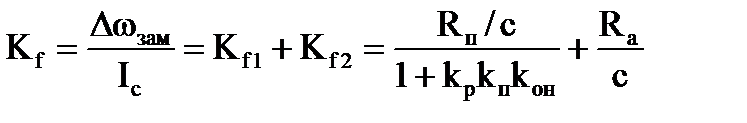(3.7)

Из (3.7) получается выражение для статической просадки скорости в замкнутой системе регулирования:

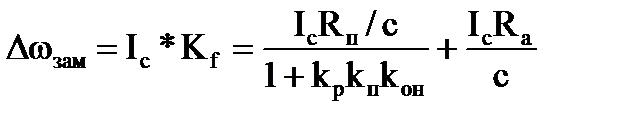. (3.8)

Рис. 3.7. Преобразования структурной схемы по возмущающему воздействию

Равенство выражений (3.3) и (3.6), (3.4) и (3.8) говорит о правильности вывода данных зависимостей.

Если скорость идеального холостого хода умножить на c = kФн, то получим выражение для определения напряжения холостого хода ТП, а если умножить на c = kФн выражение 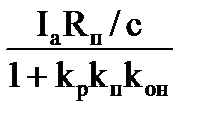, то получится уравнение для определения падения напряжения в ТП в замкнутой системе регулирования.

Поэтому, уравнение внешней характеристики ТП в замкнутой системе регулирования, в соответствии с выше сказанным, примет вид:

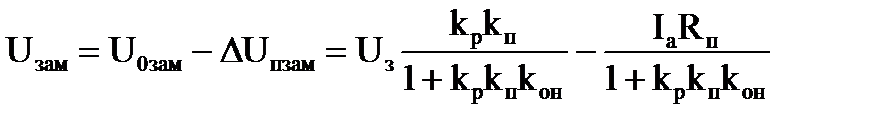(3.9)

где U0зам – напряжение холостого хода ТП при нулевом токе, ΔUпзам – падение напряжения в ТП в замкнутой системе регулирования.

Проанализируем влияние отрицательной обратной связи по напряжению на вид внешних и электромеханических характеристик электропривода.

Примем kон=0, т.е. разомкнем обратную связь. При этом для разомкнутой системы из (3.8) и (3.9) получается:

;	;
;	.

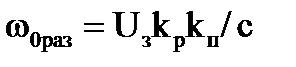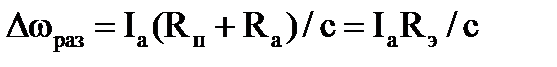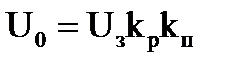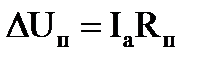Эти характеристики показаны на рис. 3.8, как характеристики 1 разомкнутой системы. Если подключить к входу регулятора (рис.3.1) отрицательную обратную связь по напряжению, т.е. k_он≠0, то изменится значение скорости идеального холостого хода (характеристика 4а на рис. 3.3) и напряжения холостого хода ТП. Увеличением U_з на входе регулятора можно установить 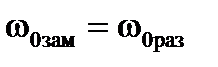и 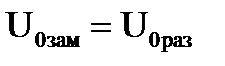, для того, чтобы все характеристики выходили из одной точки идеального холостого хода для удобства сравнения характеристик.

В соответствии с (3.8) и (3.9) подключение отрицательной обратной связи по напряжению ведет к уменьшению статической просадки скорости, т.е. увеличению жесткости электромеханической характеристики и уменьшению падения напряжения в ТП (характеристики 2 на рис. 3.8). При настройке системы регулирования изменяемыми параметрами могут быть коэффициенты передачи (усиления) регулятора и обратной связи по напряжению. Увеличение либо k_р либо k_он ведет к дальнейшему уменьшению 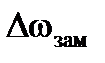и 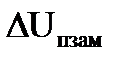. При k_р*k_он→∞ 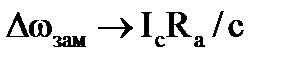, а 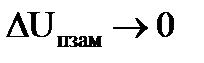, откуда видно, что предельная внешняя характеристика ТП будет абсолютно жесткой и ей соответствует естественная электромеханическая характеристика электропривода (характеристики 3 на рис.3.8). Таким образом, диапазон электромеханических характеристик в системе с отрицательной обратной связью по напряжению лежит в пределах от разомкнутой до естественной.

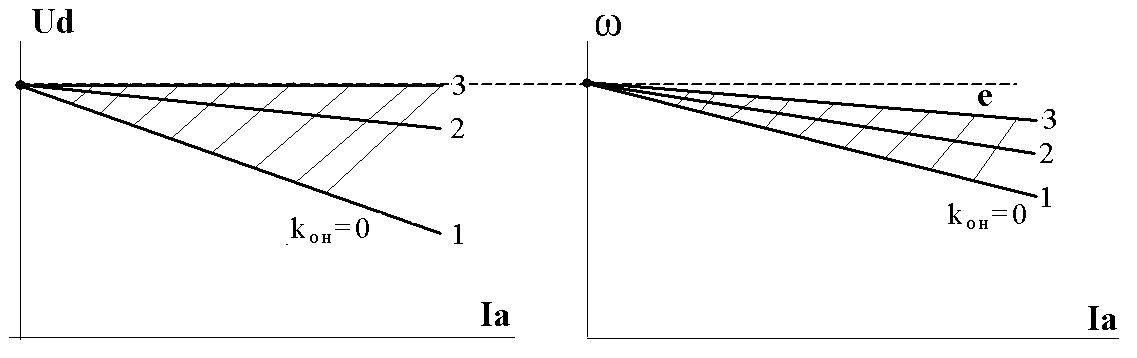Рис. 3.8. Внешние и электромеханические характеристики в системе регулирования с отрицательной обратной связью по напряжению

Из теории автоматического регулирования известно, что система регулирования будет астатической, если в канале регулирования имеется интегральная составляющая. Следовательно, применение пропорционально – интегрального (ПИ) регулятора позволит получить жесткость естественной электромеханической характеристики при реальных значениях k_р и k_он.

Несколько преобразовав выражение (3.8) легко получить следующее равенство:

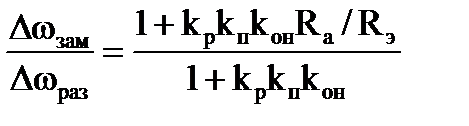, (3.10)

на основании которого можно настроить систему регулирования для получения заданной жесткости характеристики, т.е. заданного отношения 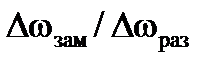, для которого при заданном значении k_он можно рассчитать требуемое значение k_р либо при заданном значении k_р рассчитать требуемое значение k_он.