Программирование конечного автомата.

Определение конечного автомата

Конечным автоматом (КА) называют пятерку следующего вида:

M(Q, V, δ, qo, F),

где

Q — конечное множество состояний автомата;

V — конечное множество допустимых входных символов (алфавит автомата);

δ — функция переходов, отображающая V*Q (декартово произведение множеств) во множество подмножеств Q: R(Q), то есть ;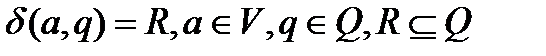

q0 — начальное состояние автомата Q, ;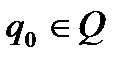

F — непустое множество конечных состояний автомата, .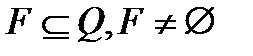

КА называют полностью определенным, если в каждом его состоянии существует функция перехода для всех возможных входных символов, то есть: .

Работа конечного автомата представляет собой последовательность шагов (или тактов). На каждом шаге работы автомат находится в одном из своих состояний Q (в текущем состоянии), на следующем шаге он может перейти в другое состоя­ние или остаться в текущем состоянии. То, в какое состояние автомат перейдет на следующем шаге работы, определяет функция переходов δ. Она зависит не только от текущего состояния, но и от символа из алфавита V, поданного на вход автомата. Когда функция перехода допускает несколько следующих состояний автомата, то КА может перейти в любое из этих состояний. В начале работы ав­томат всегда находится в начальном состоянии q0. Работа КА продолжается до тех пор, пока на его вход поступают символы из входной цепочки .

Видно, что конфигурацию КА на каждом шаге работы можно определить в виде (q,ω,n), где q — текущее состояние автомата, ; ω — цепочка входных симво­лов, 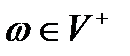; n — положение указателя в цепочке символов, (N — множество натуральных чисел). Конфигурация автомата на следующем шаге — это (q', ω, n+1), если и символ находится в позиции n + 1 цепочки ω. Начальная конфигурация автомата: (q0,ω,0); заключительная конфигурация ав­томата: (f, ω, n), , она является конечной конфигурацией, если .

Язык, заданный конечным автоматом

Конечный автомат M(Q, V, δ, qo, F) принимает цепочку символов 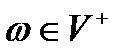, если, получив на вход эту Цепочку, он из начального состояния q0 может перейти в одно из конечных со­стояний 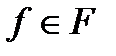. В противном случае КА не принимает цепочку символов.

Язык L(M), заданный KA M(Q,V,δ,qo,F), - это множество всех цепочек симво­лов, которые принимаются этим автоматом. Два КА эквивалентны, если они за­дают один и тот же язык. Все КА являются распознавателями для регулярных языков.

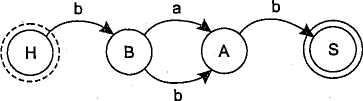
Граф переходов недетерминированного конечного автомата

Граф переходов полностью определенного недетерминированного конечного автомата

Определение детерминированного конечного автомата

Конечный автомат M(Q, V, δ, qo, F) называют детерминированным конечным автоматом (ДКА), если в каждом из его состояний для любого входного символа функция перехода содержит не более одного состояния : либо , либо .

В противном случае конечный автомат называют недетерминированным.

Из этого определения видно, что автоматы, представленные ранее на рисунках являются недетерминированными КА.

ДКА может быть задан в виде пятерки:

M(Q, V, δ, qo, F),

где

Q — конечное множество состояний автомата;

V — конечное множество допустимых входных символов;

δ — функция переходов, отображающая V*Q в множество Q: ;

q0 — начальное состояние автомата Q, ;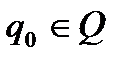

F — непустое множество конечных состояний автомата, .

Если функция переходов ДКА определена для каждого состояния автомата, то авто­мат называется полностью определенным ДКА: : либо .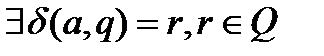

Доказано, что для любого КА можно построить эквивалентный ему ДКА. Моде­лировать работу ДКА существенно проще, чем работу произвольного КА, поэто­му произвольный КА стремятся преобразовать в ДКА. При построении компи­ляторов чаще всего используют полностью определенный ДКА.