Формальное определение грамматики и языка.

Понятие языка. Формальное определение языка

В общем случае язык — это заданный набор символов и правил, устанавливаю­щих способы комбинации этих символов между собой для записи осмысленных текстов. Основой любого естественного пли искусственного языка является алфавит, определяющий набор допустимых символов языка. Алфавит — это счетное множество допустимых символов языка. Будем обозна­чать это множество символом V. Интересно, что согласно формальному опреде­лению, алфавит не обязательно должен быть конечным множеством, но реально все существующие языки строятся на основе конечных алфавитов. Цепочка символов α является цепочкой над алфавитом V: α(V), если в нее вхо­дят только символы, принадлежащие множеству символов V. Для любого алфа­вита V пустая цепочка λ может как являться, так и не являться цепочкой λ(V). Это условие оговаривается дополнительно. Если V — некоторый алфавит, то: V⁺ — множество всех цепочек над алфавитом V без λ; V* — множество всех цепочек над алфавитом V, включая λ. Справедливо равенство: .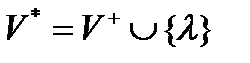

Языком L над алфавитом V: L(V) называется некоторое счетное подмножество цепочек конечной длины из множества всех цепочек над алфавитом V. Из этого определения следует два вывода: во-первых, множество цепочек языка не обяза­но быть конечным; во-вторых, хотя каждая цепочка символов, входящая в язык, обязана иметь конечную длину, эта длина может быть сколь угодно большой и формально ничем не ограничена.

Все существующие языки подпадают под это определение. Большинство ре­альных естественных и искусственных языков содержат бесконечное множество цепочек. Также в большинстве языков длина цепочки ничем не ограничена. Цепочку символов, принадлежащую заданному языку, часто называют предло­жением языка, а множество цепочек символов некоторого языка L(V) — множе­ством предложений этого языка. Для любого языка L(V) справедливо: .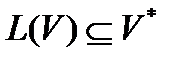

Язык L(V) включает в себя язык L`(V): , если . Множество цепочек языка L'(V) является подмножеством множества цепочек языка L(V) (или эти множества совпадают). Очевидно, что оба языка должны строиться на основе одного и того же алфавита.

Два языка L(V) и L'(V) совпадают (эквивалентны): L'(V) = L(V), если и или, что то же самое: и 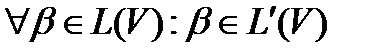. Множества допустимых цепочек символов для эквивалентных языков равны. Два языка L(V) и L'(V) почти эквивалентны: 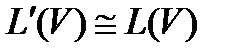, если 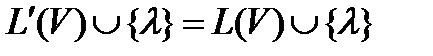. Множества допустимых цепочек символов почти эквивалентных языков могут различаться только на пустую цепочку символов.

Кроме алфавита язык предусматривает также правила построения до­пустимых цепочек, поскольку обычно далеко не все цепочки над заданным алфа­витом принадлежат языку. Символы могут объединяться в слона или лексемы - элементарные конструкции языка, на их основе строятся предложении — более сложные конструкции. И те и другие в общем виде являются цепочками симво­лов, но предусматривают некоторые правила построения. Таким образом, необ­ходимо указать эти правила, или строго говоря, задать язык. В общем случае язык можно определить тремя способами:

· перечислением всех допустимых цепочек языка;

· указанием способа порождения цепочек языка (заданием грамматики языка);

· определением метода распознавания цепочек языка.

Первый из методов является чисто формальным и на практике не применяется, так как большинство языков содержат бесконечное число допустимых цепочек и перечислить их просто невозможно. Иногда для чисто формальных языков можно перечислить множество входящих и них цепо­чек, прибегнув к математическим определениям множеств. Однако этот подход уже стоит ближе ко второму способу.

Например, запись задает язык над алфавитом V ={0,1}, содержащий все последовательности с чередующимися символами 0 и 1, начи­нающиеся с 0 и заканчивающиеся 1. Видно, что пустая цепочка символов в этот язык не входит.

Второй способ предусматривает некоторое описание правил, с помощью кото­рых строятся цепочки языка. Тогда любая цепочка, построенная с помощью этих правил из символов алфавита языка, будет принадлежать заданному языку.

Третий способ предусматривает построение некоторого логического устройства (распознавателя) - автомата, который на входе получает цепочку символов, а на выходе выдает ответ: принадлежит или нет эта цепочка заданному языку.

Говоря о любом языке, можно выделить его синтаксис и семантику. Кроме того, трансляторы имеют дело также с лексическими конструкциями (лексемами), ко­торые задаются лексикой языка. Синтаксис языка - это набор правил, определяющий допустимые конструкции языка. Синтаксис определяет «форму языка» - задает набор цепочек символов, которые принадлежат языку. Чаще всего синтаксис языка можно задать в виде строгого набора правил, но полностью это утверждение справедливо только дли чисто формальных языков. Семантика определяет «содержание языка» — задает смысл для всех до­пустимых цепочек языка. Семантика для большинства языков определяется не­формальными методами (отношения между знаками и тем, что они обозначают, изучаются семиотикой). Чисто формальные языки лишены какого-либо смыс­ла. Лексика — это совокупность слов (словарный запас) языка. Слово или лексиче­ская единица (лексема) языка — это конструкция, которая состоит из элементов алфавита языка и не содержит в себе других конструкций. Иначе говоря, лекси­ческая единица может содержать только элементарные символы и не может со­держать других лексических единиц.

Формальное определение грамматики. Форма Бэкуса—Наура

Грамматика — это описание способа построения предложений некоторого языка. Иными словами, грамматика — это математическая система, определяющая язык. Фактически, определив грамматику языка, мы указываем правила порождения цепочек символов, принадлежащих этому языку. Таким образом, грамматика — это генератор цепочек языка. Она относится ко второму способу определения языков — порождению цепочек символов.

Грамматику языка можно описать различными способами. Например, грамматика русского языка описывается довольно сложным набором правил, которые изуча­ют в начальной школе. Для некоторых языков (в том числе для синтаксических конструкции языков программирования) можно использовать формальное опи­сание грамматики, построенное на основе системы правил (пли продукций). Правило (пли продукция) — это упорядоченная пара цепочек символов (α, β). В пра­вилах важен порядок цепочек, поэтому их чаще записывают в виде α → β (или α::=β). Такая запись читается как «α порождает β» или «β по определению есть α». Грамматика языка программирования содержит правила двух типов; первые (определяющие синтаксические конструкции языка) довольно легко поддаются фор­мальному описанию; вторые (определяющие семантические ограничения языка) обычно излагаются в неформальной форме. Поэтому любое описание (или стан­дарт) языка программирования обычно состоит из двух частей: вначале фор­мально излагаются правила построения синтаксических конструкции, а потом на естественном языке дается описание семантических правил.

Язык, заданный грамматикой G, обозначается как L(G).

Две грамматики G и G' называются эквивалентными, если они определяют один и тот же язык: L(G) = L(G'). Две грамматики G и G' называются почти эквива­лентными, если заданные ими языки различаются не более чем на пустую цепоч­ку символов:

Формально грамматика G определяется как четверка G(VT,VN, P, S), где: VT — множество терминальных символов или алфавит терминальных символов; VN — множество нетерминальных символов пли алфавит нетерминальных сим­волов;

P — множество правил (продукций) грамматики, вида α → β, где ;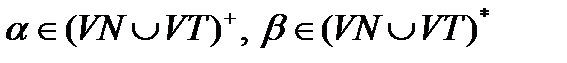

S — целевой (начальный) символ грамматики .

Алфавиты терминальных и нетерминальных символов грамматики не пересека­ются: 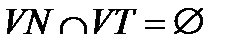. Это значит, что каждый символ в грамматике может быть либо терминальным, либо нетерминальным, но не может быть терминальным и нетерминальным одновременно. Целевой символ грамматики — это всегда не­терминальный символ. Множество называют полным алфавитом грамматики G.

Во множестве правил грамматики может быть несколько правил, имеющих оди­наковые левые части, вида: α → β₁, α → β₂,.. α → β_n. Тогда эти правила объеди­няют вместе и записывают в виде: α → β₁| β₂|…| β_n. Одной строке в такой записи соответствует сразу n правил.

Такую форму записи правил грамматики называют формой Бэкуса—Наура. Форма Бэкуса—Наура предусматривает, как правило, также, что нетерминальные симво­лы берутся в угловые скобки: < >.

АСУЖТ

АРМы.

АРМ – совокуп. программ., методич. и языковых ПС, обеспечивающих работу польз. на пк в некот. предметн. обл. Структура АРМ - это совокупность его подсистем и элементов.

К подсистемам обеспечения в первую относ.: техническую, информационную, программную и организационную. Кроме того, существует целый, ряд других подсистем.

Техническое обеспеч предст. собой комплекс технических средств, основой которого служит ПЭВМ К комплекту техноло­гических средств следует отнести средства телефонной связи.

Инф. обеспеч- это мас­сивы информации, хранящиеся в локальных базах данных. Управление инф. осуществляется с помощью программной системы управления базами данных, которая производит запись информации, поиск, считывание, корректировку и решение информационных задач. ПО состоит из сис­темного программного обеспечения и прикладного. Основой системного обеспечения являются операционные системы (ОС) и системы программи­рования, например, алгоритмические языки Ассемблер, ПЛ/1, Бейсик и др. Системные программы обеспечивают рациональную технологию • обработки информации.

Прикладное программное обеспе­чение сост. стандартные программы пользователей и па­кеты прикладных программ разного назначения. Стандартные программы пользователей представляют собой программы решения оп­ределенных задач на алгоритмических языках.

АРМ ДСП – дежурного по стан.

АРМ ДСЦ- маневрового диспетчера

АРМ ТКО – оператора техн. конторы по отправл.

АРМ ТКП – то же по прибытию

АРМ ТВК – товарного кассира

АРМ ПС- приемосдатчиков груза

АРМ КП –оператора контейнерной площадки